Lesson

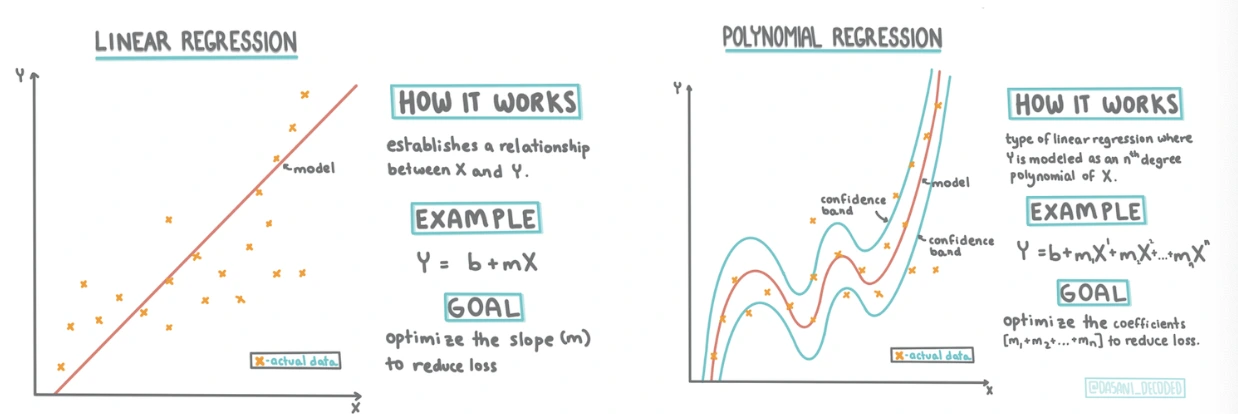
이 레슨에서는 호박의 가격을 선형회귀하는 방법을 소개한다.

Linear부터 Polynomial회귀 및 여러 predictor들을 추가해가며 정확도를 높이는 practice가 있다.

Simple Linear RegressionPermalink

이건 Simple Linear Regression 글을 참고하자.

CorrelationPermalink

Correlation Coefficient는 변수들간에 얼마나 상관성이 있는지 수치화한 값이다.

이 값은 $-1 \sim 1$ 이며 0에 가까울수록 상관이 없다는 것을 의미한다. $1$ 이면 매우 강한 양의 상관, $-1$ 이면 매우 강한 음의 상관관계를 의미한다.

pandas에서 corr 함수로 계산할 수 있으며 기본적으로 피어슨 상관계수(Pearson Correlation Coefficient)로 계산된다.

print(new_pumpkins['Month'].corr(new_pumpkins['Price']))
print(new_pumpkins['DayOfYear'].corr(new_pumpkins['Price']))

matplot에서 각 범주별로 색을 다르게 scatter하기Permalink

ax=None
colors = ['red','blue','green','yellow']
for i,var in enumerate(new_pumpkins['Variety'].unique()):
    df = new_pumpkins[new_pumpkins['Variety']==var]
    ax = df.plot.scatter('DayOfYear','Price',ax=ax,c=colors[i],label=var)

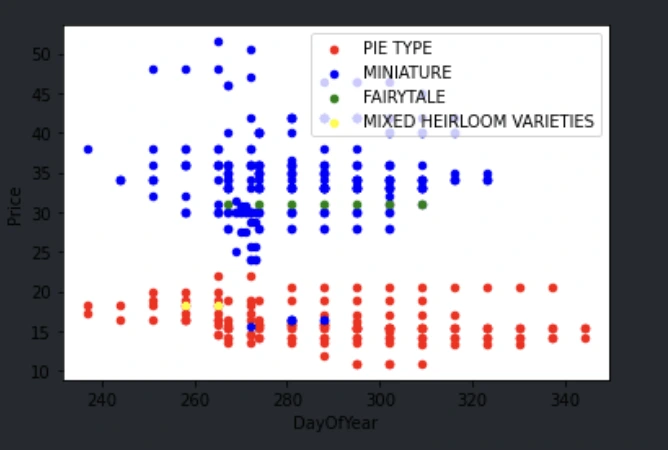
위는 DataFrame에서 바로 plot을 그리는 예시인데, ax에 동일한 Axis를 계속 전달하며 색상을 바꿔주는 모습이다.

또한 new_pumpkins[new_pumpkins['Variety']==var] 과 같은 코드를 이용해 loc을 쓰지 않고도 단순히 Variety column이 var 인 행들을 필터링할 수 있다.

Pandas에서 그룹을 지어 값을 추출하기Permalink

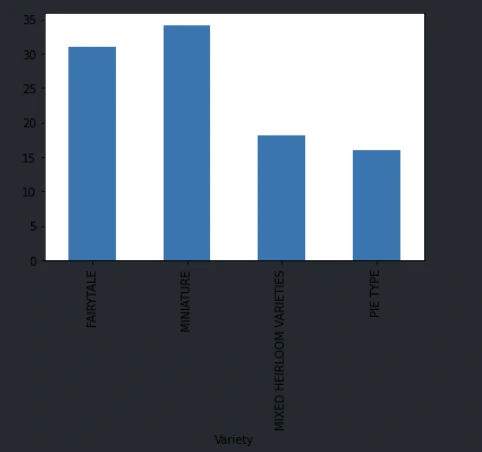
new_pumpkins.groupby('Variety')['Price'].mean().plot(kind='bar')

이 코드는 Variety별로 그룹을 나누어 Price Column에 대한 평균값을 바 차트로 그려주는 코드이다.

One-Hot EncodingPermalink

One-Hot Encoding은 카테고리화된 변수들을 Numerical하게 변경해주는 테크닉이다.

우리가 회귀모델을 만드려면 predictor는 numerical하게 존재해야 하기 때문이다.

그중에서도 One-Hot Encoding은 각 범주마다 Column을 하나 추가해서 1과 0으로 값을 채운 Data Frame을 만드는 방식이다.

A,B,C,D 를 $1,2,3,4$로 바꾸는 방법도 있지만 $1,2,3,4$ 값을 그대로 사용하면 이 값의 크기때문에 회귀가 제대로 수행되지 않을 수 있기 때문에 아예 독립적인 Column으로 빼내는 것이다.

pandas에서 get_dummies 함수를 이용해 수행할 수 있고 .join 함수로 만들어진 결과들을 다시 Data Frame에 추가할 수 있다.

X = pd.get_dummies(new_pumpkins['Variety']) \
        .join(new_pumpkins['Month']) \
        .join(pd.get_dummies(new_pumpkins['City'])) \
        .join(pd.get_dummies(new_pumpkins['Package']))

MSE, 오차비율, 결정계수Permalink

MSE는 Mean Square Error로 오차의 제곱을 평균낸 값으로 모델의 정확도를 측정하는데 사용되는 값이다.

또한 이를 평균으로 나눈값이 오차비율이라고 하는 상대적 에러 크기를 나타낸다.

마지막으로 Coefficient of Determination(결정계수)는 모델의 score 함수로 얻어올 수 있다.

결정계수는 $R^2$ 라고도 불리며 $R^2=1-\dfrac{SSE}{SST}$ 로 계산된다. 이 값은 $0 \sim 1$에 존재하며 $1$에 가까울 수록 좋은 모델이다.

pred = lin_reg.predict(X_test)

mse = np.sqrt(mean_squared_error(y_test,pred))
print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)')

score = lin_req.score(X_train, y_train)
print(score)

여기서 MSE는 y_test, pred로 구하고 score엔 X_train, y_train을 넣는 이유는 위 코드에선 그저 $R^2$를 훈련 데이터에 대해서 얻고싶기 때문이다.(학습 데이터에 대한 모델 성능 확인)

Simple Linear Regression 구현Permalink

scikit-learn에서 제공하는 LinearRegression 클래스를 이용해 선형회귀분석을 진행할 수 있다.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

이렇게 LinearRegression 클래스와 MSE를 구해줄 sklearn.metrics의 mean_squared_error 함수, Train와 Test 데이터 셋을 나눠줄 sklearn.model_selection의 train_test_split 함수를 불러와준다.

선형회귀분석을 할 때는 Predictor 데이터가 2차원 배열이 되어야 하므로 numpy의 reshape를 이용해 구조를 바꿔준다.

X = pie_pumpkins['DayOfYear'].to_numpy().reshape(-1,1)
y = pie_pumpkins['Price']

이제 train_test_split 함수를 이용해 데이터를 훈련용과 테스트용으로 분리하고,

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

LinearRegression의 fit 함수를 이용해 모델을 학습시킨다.

lin_reg = LinearRegression()
lin_reg.fit(X_train,y_train)

모델의 성능 측정은 다음과 같이 위에서 설명한 방법대로 할 수 있다.

pred = lin_reg.predict(X_test)

mse = np.sqrt(mean_squared_error(y_test,pred))
print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)')

score = lin_req.score(X_train, y_train)
print(score)

Polynomial RegressionPermalink

다항회귀는 선형회귀처럼 직선이나 평면이 아닌 곡선이 plot에 포함된다고 생각하면 된다.

수학적으로 다항식에서 2차항을 가진다면 Polynomial Regression이라고 분류할 수 있다.

어떤 데이터의 특징은 항상 선형으로만 이루어질 수 없기 때문에 $x^2, x^3$ 같은 2차 이상의 항들이 predictor로 포함되어 같이 학습될 수도 있다.

$x, x^2$ 와 같이 같은 변수가 차수만 다르게 다른 항으로 모델에 존재할 수 있다.

이걸 코드화하면 다음과 같이 LinearRegression에 pipeline을 이용해 PolynomialFeatures(n) 을 추가해주면 된다.

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline

pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression())

pipeline.fit(X_train,y_train)

PolynomialFeatures는 항들의 convolution을 만들어주는 역할인데, $x_1, x_2$ 가 predictor로 있다면 $x_1, x_2, x_1x_2, x_1^2, x_2^2$ 와 같이 항들을 확장시켜준다.

하지만 이 레슨에선 애초에 date와 price간의 correlation coefficient가 높지 않기 때문에 Polynomial Regression을 써도 모델의 성능이 크게 향상되지 않는다.

그래서 이 레슨에선 One-Hot Encoding을 이용해 여러 Predictor를 이용해 Polynomial Regression까지 사용해 정확도를 높여 마무리한다.

Final CodesPermalink

이 레슨의 최종 코드는 다음과 같다.

# set up training data
X = pd.get_dummies(new_pumpkins['Variety']) \
        .join(new_pumpkins['Month']) \
        .join(pd.get_dummies(new_pumpkins['City'])) \
        .join(pd.get_dummies(new_pumpkins['Package']))
y = new_pumpkins['Price']

# make train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# setup and train the pipeline
pipeline = make_pipeline(PolynomialFeatures(2), LinearRegression())
pipeline.fit(X_train,y_train)

# predict results for test data
pred = pipeline.predict(X_test)

# calculate MSE and determination
mse = np.sqrt(mean_squared_error(y_test,pred))
print(f'Mean error: {mse:3.3} ({mse/np.mean(pred)*100:3.3}%)')

score = pipeline.score(X_train,y_train)
print('Model determination: ', score)