Linear Regression - 단순선형회귀(Simple Linear Regression) 2
Best Fitting Line
Simple Linear Regression에서 최고의 fitting line을 선정하는 기준은 무엇일까?
scatter plot을 그렸을 때 가장 적절해보이는 선을 선택할 수도 있을 것이다.
그러나 수학적으로 결정하는 방법들이 있다.
다음과 같은 plot을 보자.
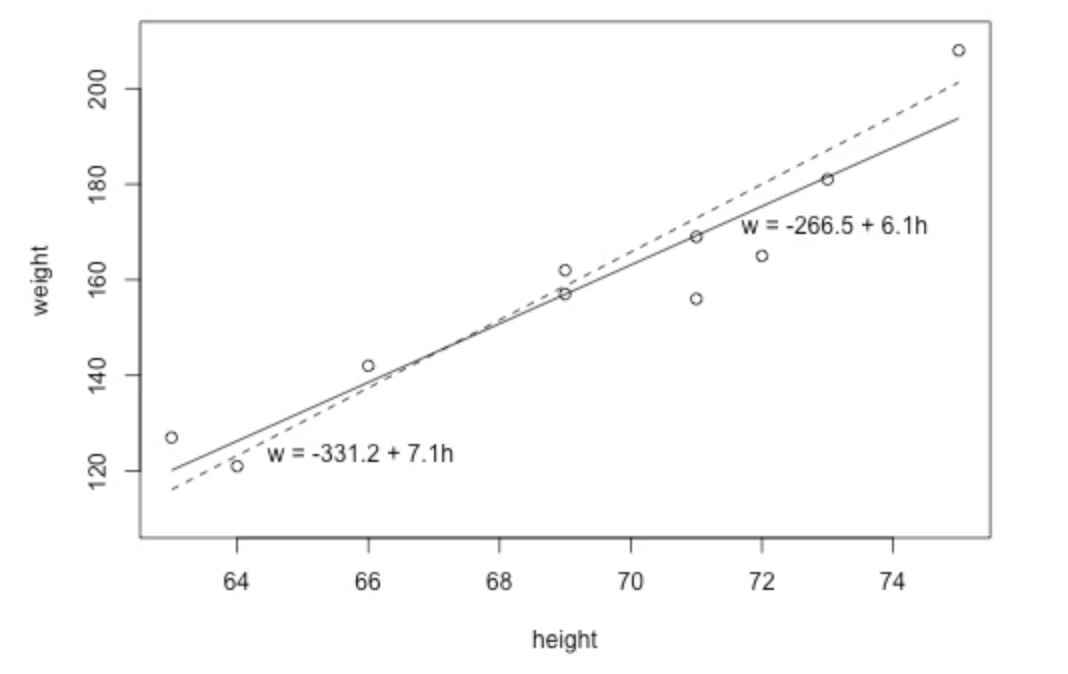
몇가지 notation을 알고가자.
- $y_i:$ 관측된 response의 값이다.
- $x_i:$ 관측된 predictor의 값이다.
- $\hat{y_i}:$ 예측된 response의 값이다.
따라서 최적의 fitting line은 다음과 같은 방정식을 만족한다.
Prediction Error
하지만 Statistical Relationship의 특성상, 그리고 머신러닝의 특성상 오차가 절대 없는 모델은 없다.
따라서 키가 $63$ inch인 학생을 방정식에 넣어보면 $\hat{y}=120.1$이 나오지만 실제로는 학생의 몸무게는 그 값이 아니다.
이를 Prediction Error(예측 오차) 혹은 Residual Error(잔차 오차) 라 부른다.
따라서 $e_i=y_i-\hat{y_i}$ 이다.
Best Fitting Line?
따라서 $\displaystyle \sum_{i=1}^{n}e_i$ 가 최소가 되는 모델이 최고의 모델일 것이다.
이 오차를 계산하는 방법중 하나는 least squares criterion 로, 오차들의 제곱의 합을 이용하는 것이다.
즉, $Q=\displaystyle \sum_{i=1}^{n} \left( y_i-\hat{y_i} \right)^2$ 를 최소로 해야한다.
제곱을 하는 이유는 $y_i-\hat{y_i}$를 할 때 음수와 양수가 모두 나올 수 있어 오차가 줄어드는 현상을 막기 위해서이다.
이를 Sum of Square Error(SSE) 라고도 부른다.
최적의 계수들을 결정하기
그럼 무한히 많은 직선에 대해서 $Q$가 최소가 되는 직선을 찾아야할까?
아니다. 이는 미적분을 이용하거나 나중에 배울 경사하강법을 이용해 구할 수 있다.
미적분을 이용하는 방법을 다루진 않지만, 대략
에서 $b_0$와 $b_1$에 대해서 미분하고 연립방정식을 푸는 방식이다.
하지만 우리가 직접 모델링을 할 때는 Minitab이나 sklearn같은 소프트웨어를 사용하면 된다.
그러면 이런 결과가 나온다.
Residual Error(잔차오차)의 합이 $597.4$ 이고 intercept와 coefficient가 각각 $-266.53,~6.1376$이 나온것을 볼 수 있다.
$b_0$(constant)는 우리에게 무엇을 말할까? $h=0$이라면 몸무게가 $-267$파운드가 되는데 이건 말도안된다.
그러나 이건 scope of the model을 넘어서는 extrapolated된 측정이기 때문에 우리가 학습시킨 모델에 있어서 의미가 없다.
Comments