PrerequisitePermalink

• Segment Tree or Fenwick Tree
• Merge Sort

Inversion CountingPermalink

Inversion Counting은 원소의 종류는 같고 순서만 다르게 배치되어 있을 때, $f(x)$ 로 선을 그으면 특정 두 원소간에 순서가 교차하는 것의 개수이다.

문제에 따라 수의 중복이 있을 수 있다. 그에 따라 구현을 적절히 신경써줘야 한다.

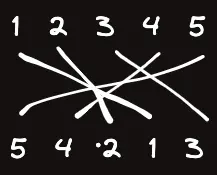
위와 같은 그림에서 각 선분이 교차하는 부분의 개수이다.

이걸 이용하면 다양한 문제를 해결할 수 있는데, 그건 이따 살펴보고 이 개수를 어떻게 세는지 먼저 살펴보자.

구간합 트리로 세기Permalink

구간합 세그먼트 트리나 펜윅 트리를 이용해 세줄 수 있다.

위의 그림을 이용해 세준다고 해보자.

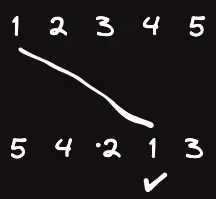
일단 1에서 1로 갔고 아래쪽에 방문되었다는 표시의 체크를 했다.

이제 2에서 2로 갈건데, 이 때는 기존 1과 교차하게 된다.

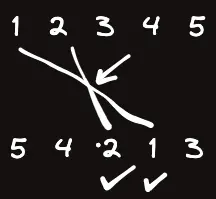
이 때, 바로 $f(2)$ 에서 끝 까지 체크되어있는 것의 개수를 정답에 더해줌으로써 교차하는 것의 개수를 셀 수 있다.

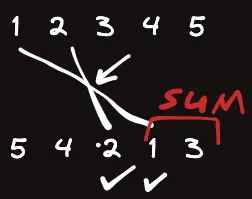
이런 방식으로 끝까지 세주면 되고 이를 구간합 트리로 구현하면 된다.

구간합 쿼리가 $O(\log N)$ 이라고 할 때, 결국 끝까지 모두 세면 $O(N\log N)$ 이 걸린다.

병합 정렬로 세기Permalink

$f$ 를 다시 기존 수열로 되돌리는 정렬 과정에서 병합 정렬을 사용하면 이 수를 세줄 수 있다.

두 배열을 합칠 때 더 오른쪽에 있던 배열 $R$ 의 원소 $r$ 이 합쳐져야 할 배열 $T$ 의 다음 자리로 갈 때, 왼쪽에 있던 배열 $L$ 에서 아직 $T$ 로 가지 못한 원소의 수를 정답에 세주는 것이다.

병합 정렬은 $O(N\log N)$ 이므로 이 때도 시간복잡도는 같다.

정렬된 두 배열 $L$ 과 $R$ 이 있고 $L=\{1,4,5,7\} ~~ R=\{2,3,6,8\}$ 라고 하자.

병합 정렬 과정에서 다음과 같이 진행된다.

$L={\color{salmon}1},4,5,7~~R=2,3,6,8\\T=1$

이건 $L$ 에서 $T$ 로 이동한 것이므로 정답을 세주지 않는다.

이제 $R$ 에서 $2$ 가 $T$로 이동한다.

$L={\color{salmon}1},4,5,7~~R={\color{salmon}2},3,6,8\\T=1,2$

이 때, $L$ 에는 아직 이동되지 못한 원소 $3$ 개가 있으므로 정답에 3을 더해준다.

이 이동하지 못한 원소들은 언젠간 $T$ 로 갈텐데 그럼 $R$ 에서 먼저 $T$ 에 가있었던 $2$ 와 계속 한 번씩 교차될 것이기 때문에 세주는 것이다.

$L={\color{salmon}1},4,5,7~~R={\color{salmon}2, 3},6,8\\T=1,2,3$

정답에 또 3이 더해진다.

$L={\color{salmon}1,4},5,7~~R={\color{salmon}2, 3},6,8\\T=1,2,3,4$

$L={\color{salmon}1,4, 5},7~~R={\color{salmon}2, 3},6,8\\T=1,2,3,4,5$

이번엔 두개가 $L$ 에서 왔으므로 정답은 그대로이다.

$L={\color{salmon}1,4, 5},7~~R={\color{salmon}2, 3,6},8\\T=1,2,3,4,5,6$

정답에 $L$ 에 남은 원소의 수 1을 더해주게 되고,

$L={\color{salmon}1,4, 5,7}~~R={\color{salmon}2, 3,6,8}\\T=1,2,3,4,5,6,7,8$

더 교차되는 것 없는채로 알고리즘이 종료된다. 총 inversion counting 횟수는 $7$ 이다.

이를 구현한 코드는 다음과 같다.

vi a = {1, 4, 5, 7, 2, 3, 6, 8};  
int ans = 0;  
  
function<void(int, int)> merge_sort = [&](int l, int r) -> void {  
   if (l >= r) return;  
   int m = l + r >> 1;  
   merge_sort(l, m);  
   merge_sort(m + 1, r);  
  
   vi T(r - l + 1);  
  
   for (int i = l, j = m + 1, t = 0; t < sz(T); t++) {  
      if (j == r + 1 || (i != m + 1 && a[i] < a[j])) T[t] = a[i++];  
      else {  
         T[t] = a[j++];  
         ans += m + 1 - i; // here  
      }  
   }  
   for (int i = 0; i < sz(T); i++) a[l + i] = T[i];  
};  
merge_sort(0, sz(a) - 1);

활용 1 - Inversion Counting 세기Permalink

정말 말 그대로 Inversion Counting을 세는 문제들도 많다.

BOJ 10090 - Counting Inversions 도 있고,

BOJ - 7578 를 보자.

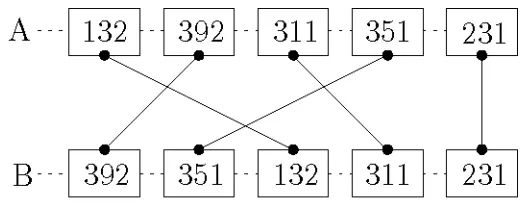
배치가 이렇게 되어있고 교차하는 선 쌍의 수를 세라는 문제이다.

펜윅 트리를 이용해서 풀면 다음과 같다.

int n;  
cin >> n;  
vi a(n), b(n);  
fv(a);  
fv(b);  
vi compress = a;  
uniq(compress);  
for (int &i: a) i = lbi(compress, i);  
for (int &i: b) i = lbi(compress, i);  
  
vi to(n), idx(n), tree(n + 1);  
  
for (int i = 0; i < n; i++) idx[a[i]] = i;  
for (int i = 0; i < n; i++) to[idx[b[i]]] = i;  
  
ll ans = 0;  
for (int i = n - 1; i >= 0; i--) {  
   int j = to[i] + 1;  
   while (j) {  
      ans += tree[j];  
      j -= j & -j;  
   }  
  
   j = to[i] + 1;  
   while (j <= n) {  
      tree[j]++;  
      j += j & -j;  
   }  
}  
cout << ans;

구간합 쿼리를 이용해 Inversion Counting을 세줄 때, $0 \to n-1$ 로 가는게 아닌 $n-1 \to 0$ 으로 가면 뒤에 체크된 것을 세는게 아닌 앞에 체크된 것을 세는 구현으로 바꿀 수 있기 때문에 쿼리를 $[0,\,to_i]$ 의 구간합을 구하면 되기 때문에 편하다.

활용 2 - 순열의 기우성Permalink

$\sigma(x)=x$ 인 순열 $\rm P$ 에서 어떤 순열 $\rm Q$ 로 변환하기 위해 임의의 두 원소 $x,\,y~~\small (x\ne y)$ 를 스왑하는 연산을 할 때, 그 연산의 횟수는 $\rm Q$ 에 따라 항상 홀수이거나 항상 짝수이다.

그리고 이것의 기우성은 Inversion Counting의 기우성과 동치이다.

이 블로그 에서 증명을 참고할 수 있다.

하지만 순열의 기우성을 구하는 것이 꼭 Inversion Counting으로 구현되어야 하는것은 아니고 짝수 길이의 싸이클을 찾는 것으로 $O(N)$ 에 수행될 수도 있으니 참고하자.

PS에선 이러한 성질을 이용해 어떤 순열 $\rm Q$ 에서 어떤 순열 $\rm R$ 로 위와 같은 연산을 통해 도달 할 수 있는지를 물어보는 문제들이 있다.

대표적으로 BOJ 5000 - 빵 정렬 이 있다.

이러한 문제들의 특징은 문제에서 설명하는 연산이 결국 위 연산과 동치라고 보아도 무방하다고 증명하기 어렵게 만들어 두었다는 점이다.

예를 들어, 어떤 연산 $\sigma$ 를 $0$번 이상 할 수 있는데, $\sigma$ 가 결국 임의의 두 원소를 스왑하는 연산을 짝수번을 하는 것과 동치라든지 하는것을 보이는 것이 쉽지 않을 수도 있다.

짝수번을 스왑하면 기우성이 변하지 않기 때문이다.

물론 짝수번 스왑하는 것이 임의의 두 원소를 교체하는 연산 두번을 하는것과는 엄연히 다르지만 결국 문제 by 문제기 때문에 이 연산을 가한다는 행위가 기우성을 판단하는 것과 연관이 있다는 것을 캐치해내면 된다.

증명Permalink

왜 순열의 기우성과 Inversion Counting의 기우성이 동치인지를 증명한다.

임의의 순열 $\rm P$ 이 $\rm P_a\cdots P_b \cdots P_c$ 라고 할 때, $a$ 와 $c$ 를 교환한다고 했을 때 $i<a$ 거나 $i>c$ 인 $i$ 는 영향받지 않는다.

이 수열의 Inversion counting이 $I$ 라고 할 때, $\rm P_a<P_c$ 라면 $I$ 가 $1$늘어나고 반대라면 $1$감소가한다.

임의의 $b~(a<b<c)$ 에 대해 $\rm P_a<P_b$ 였다면 $I$ 가 $1$늘어나고 반대라면 $1$감소한다. $\rm P_b < P_c$ 라면 $I$ 가 $1$증가하고 반대라면 $1$감소한다.

따라서 $a$와 $c$ 사이의 모든 원소들은 $a,\,c$ 의 교환으로 인해 $I$ 에 $\lvert 2 \rvert \text{ 혹은 } 0$ 의 영향을 미치므로 $I$의 기우성에 영향을 주지 않고 오직 $a,\,c$ 만이 기우성에 영향을 줘 한 번의 교환으로 기우성이 무조건 변하게 된다는 것이 보여진다.

$\sigma(x)=x$ 인 순열 $\rm P’$ 에서 시작해 $\rm P$ 로 가는 교환 과정을 거치면 $I$ 의 기우성과 $\rm P$의 기우성이 동일하게 바뀌므로 $\rm P$의 기우성과 $I$ 의 기우성은 동치이다. $\blacksquare$