Fenwick Tree
펜윅 트리
펜윅 트리는 구간합 쿼리와 업데이트 쿼리를 $O(logN)$에 하게 해주는 자료구조이다.
특히 비트를 쓰고 대개 반복문으로 구현되기 때문에 상수적으로 이점이 있는 편이다.
이 자료구조를 가지고 이것저것을 할 수 있다.
뭔가 목차가 많은데, 점 업데이트 구간 쿼리 펜윅 트리를 먼저 익히고 나면 나머지는 다 그 응용이니 걱정하지말자!
비트 연산 (bonus)
트리의 구조를 보기에 앞서, 기본적으로 알아야 할 비트 연산은 다음과 같다.
N & -N 로 N 의 마지막 비트만 얻어올 수 있다는 것이다.
N=00001010 이면, -N 은 2의 보수법에 의해 -N=11110110 이 되고
00001010
& 11110010
----------
00000010
이 됨이 보여진다.
트리의 구조
트리는 일단 $N$ 개의 데이터를 저장하는데, 길이 $N$ 의 배열만 필요하다. 세그먼트 트리같은 경우 $N\log N$이 필요한 것에 비해 더 효율적이다.
그럼 이 길이 $N$개 짜리 배열에 데이터들을 어떻게 저장해두고 있어야 할까?
$A_i$ 가 원래 기존 배열, $T_i$ 가 펜윅 트리내에 저장된 배열이라고 한다면,
배열의 원소 $A_1 \sim A_n$ 이 있을 때, $T_i$ 는 $A_i$부터 앞으로 i & -i 개의 합이 저장되어있다.
다음과 같은 그림을 보자.
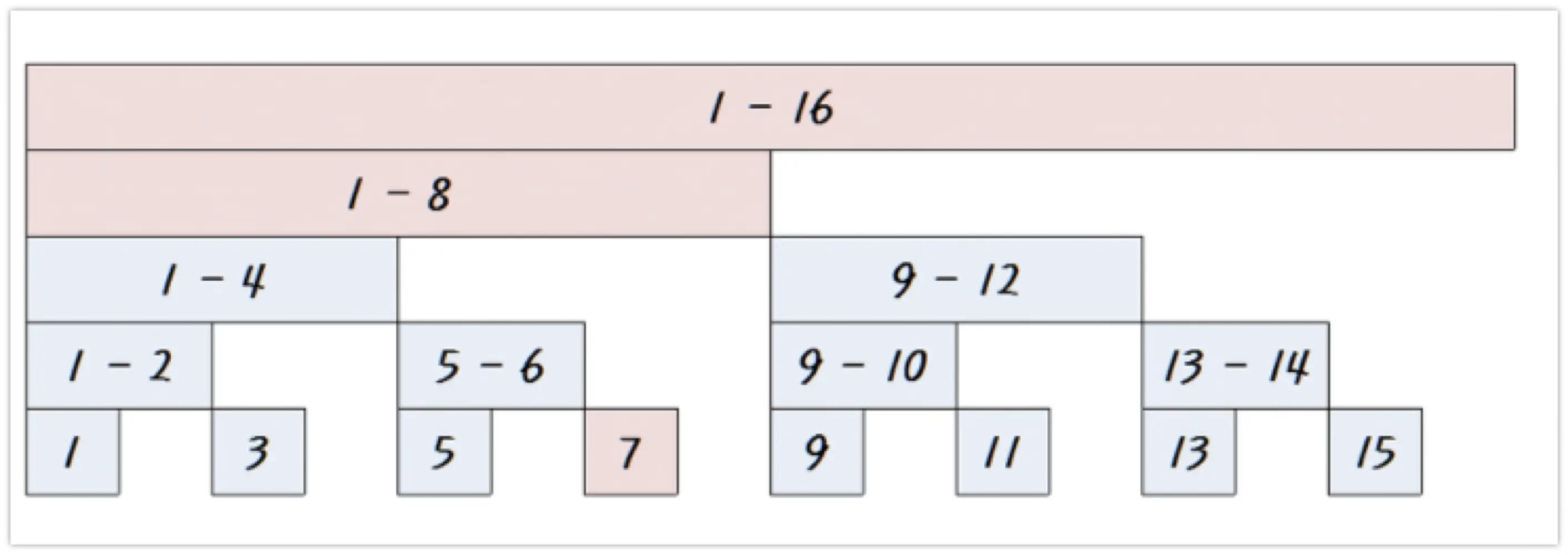
가장 쉽게 $i=16$ 일 때를 본다면, $i$ 의 가장 큰 비트는 $2^4(=16)$이므로 $1\sim16$ 까지의 값이 저장이 되어있다.
$i=12$ 라면 12=1100 이기 때문에 길이가 $4$가 되어 $9,\,10,\,11,\,12$ 의 값들의 합이 저장된다.
홀수들 같은 경우는 무조건 $2^0$ 이 존재하기 때문에 N & -N 를 해도 1이여서 자기 자신의 값만 저장하고 있는 것을 볼 수 있다.
이제 이렇게 저장된 $T$ 배열을 갖고 어떻게 쿼리들을 수행할 수 있는지 살펴볼 것이다.
Usage 1 - 점 업데이트, 구간 쿼리
말 그대로 특정 인덱스 $i$ 의 현재 값을 $O(\log N)$에 얻어오고 특정 구간 $[L, R]$ 의 합도 $O(\log N)$ 에 얻어올 수 있는 가장 기본적인 펜윅 트리의 구조이다.
우리가 $L$ 부터 $R$ 까지의 합을 알고 싶다고 하면, 이건 $[1, R]$ 구간에서 $[1, L-1]$ 구간을 빼주는 합과 동일하다.
그리고 만약 우리가 $[1,\,11]$의 합을 구해주고 싶다면, 다음과 같이 구할 수 있다.
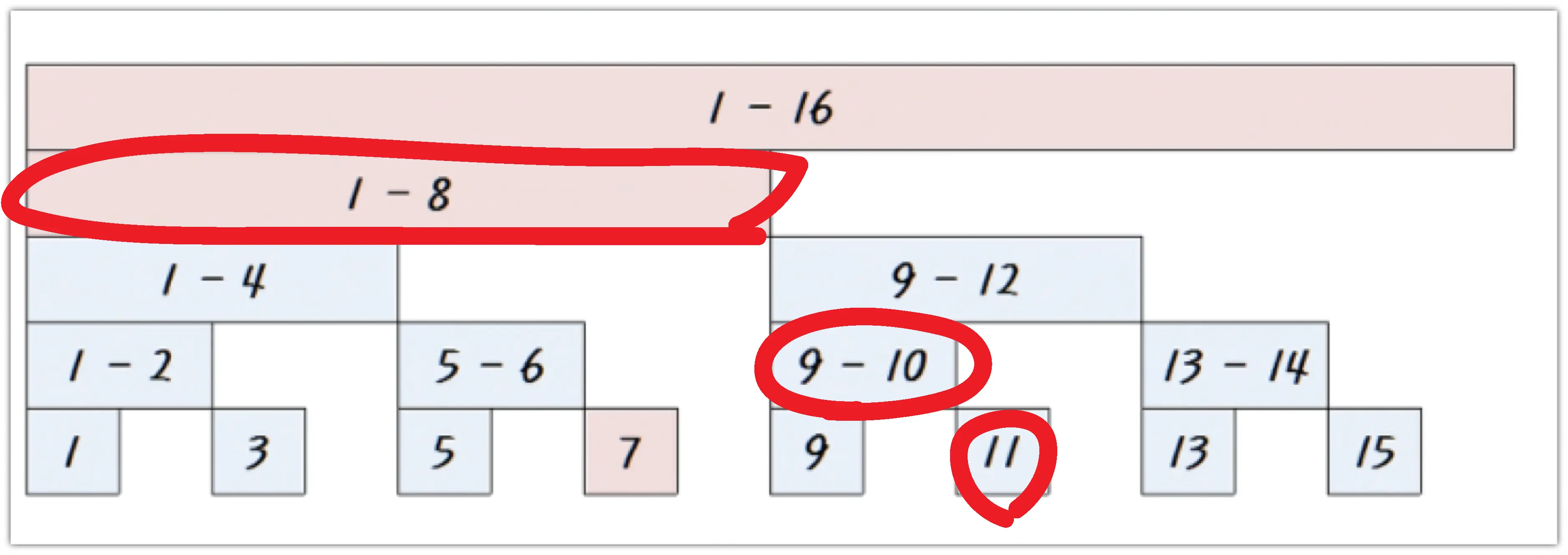
그리고 이는 놀랍게도 다음과 같이 구현된다.
int sum(int i) {
int ret = 0;
while(i) {
ret += T[i];
i -= i & -i;
}
return ret;
}
이는 명백히 $O(\log N)$ 이다. while 문이 $\log_2 N$ 번만에 끝나기 때문이다.
이걸 $R$ 과 $L-1$에 대해서 구해준다음 값을 구해주면 되니 구간 합을 $O(\log N)$ 에 구할 수 있다는 것이 보여진다.
다음은 점 업데이트이다.

여기서 11을 업데이트 하고 싶다고 하자. 그럼 우린 11을 포함하는 $i$들이 어떤것들이 있는지를 알아야 하는데, 그림에서 그냥 위로 쭉 긋기만 하면 된다.
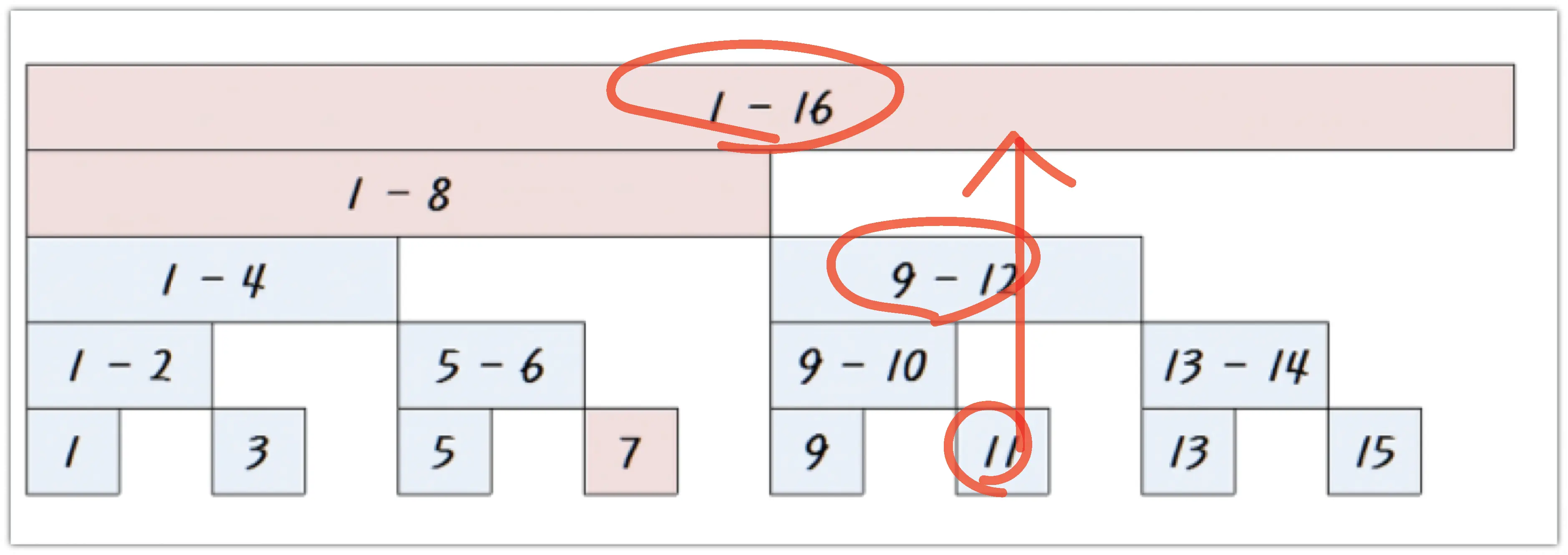
그렇다, 바로 11, 12, 16이 업데이트가 되어야 할 칸들임을 알 수 있다.
이것은 시작되는 $i$ 에서 i & -i 를 계속해서 자신에게 더함으로써 모두 순회할 수 있고, 시간복잡도는 볼 것도 없이 $O(\log N)$ 이 된다.
void update(int i, int v){
while(i <= N){
T[i] += v;
i += i & -i;
}
}
이제 실제로 완성된 구현을 하고 문제를 가볍게 하나 풀어보자.
필자는 개인적으로 struct 나 class 를 만들어 관련 연산들을 모아둔 클래스를 만들어두고 사용하는 것을 선호한다.
좀더 코드가 깔끔한 버전으론 다음과 같다.
template<class T>
struct fenwick {
int n;
vector<T> tree;
fenwick(int n) : n(n) { tree.resize(n + 1); }
T sum(int i) {
T ret = 0;
for (; i; i -= i & -i) ret += tree[i];
return ret;
}
void update(int i, T x) { for (i++; i <= n; i += i & -i) tree[i] += x; }
T query(int l, int r) { return l > r ? 0 : sum(r + 1) - sum(l); }
};
펜윅 트리는 보통 1-based index로 구현한다. 이 구현체를 사용할 땐 0-based 로 호출을 해주는 것을 가정하고 만들었기 때문에 1씩 더해주었다고 보면 된다.
연습 문제
이제 실제로 문제를 풀어보도록 하자.
이렇게 펜윅 트리를 이용해 구간합을 구하는 문제를 풀 수 있다.
펜윅 트리는 따로 init 같은 함수를 만들기가 까다로워서 그냥 $O(N\log N)$에 초기화를 시켜주면 된다.
Usage 2 - 점 쿼리, 구간 업데이트
그 다음을 살펴보자. 이건 위의 연산을 반대로 하는 것이다.
앞서 살펴본건 점을 업데이트하고 구간을 쿼리하는 것이였는데, 이건 반대로 점을 쿼리하고 구간을 업데이트하는 것이다.
이것도 펜윅 트리를 하나를 이용해서 구현이 가능하다.
위에 있는 구현체를 그냥 쓰면 된다.
아이디어는, $[L,\,R]$ 를 $d$ 만큼 증가시키는 업데이트를 하는 연산에 대해서 $T_L$ 에 $d$ 를 증가, $T_{R+1}$ 에 $-d$ 를 증가시켜두고, $k$ 번째 수가 현재 몇인지 찾는 연산에서 $\displaystyle \sum_{i=1}^k T_i$ 를 구해주는 것이다.
이 방법도 결국 두 쿼리 모두 시간복잡도가 $O(\log N)$ 임을 알 수 있다.
펜윅 트리가 원래 하는일이 구간합을 구해주는 것이기 때문이다.
| $i$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| $v_i$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $t_i$ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
라고 해보자.
이제 $[2,\,5]$ 에 3씩 더해준다고 하면,
| $i$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| $v_i$ | 0 | 0 | 3 | 3 | 3 | 3 | 0 | 0 |
| $t_i$ | 0 | 0 | 3 | 0 | 0 | 0 | -3 | 0 |
이 된다.
이제 $i=4$의 값을 구하고 싶다고 해보자. $\displaystyle \sum_{i+1}^k T_i$ 가 정말 그 값을 가리키고 있음을 쉽게 알 수 있을 것이다. $t_i=3$ 인 점을 한 번 만나 3이 되기 때문이다.
간혹 문제들에서 구간 쿼리가 필요 없이 점 쿼리, 구간 업데이트가 필요한 문제에서 이 방식으로 문제를 해결할 수 있기 때문에 “Lazy Propagation Segment Tree가 필요없어요” 하는 식의 의견들을 많이 볼 수 있는데, 이러한 테크닉을 의미하는 것 같다.
필자는 다음과 같이 템플릿으로 활용한다.
template<class T>
struct fenwick {
...
};
template<class T>
struct fenwick_point {
fenwick<T> f;
fenwick_point(int n) : f(fenwick<T>(n + 1)) {}
void update(int l, int r, T x) { f.update(l, x), f.update(r + 1, -x); }
T query(int i) { return f.query(0, i); }
};
Usage 3 - 구간 쿼리, 구간 업데이트
여기부터는 펜윅 트리를 두 개를 써서 구현해야 한다.
위에서 살펴본 테크닉과 크게 다르지 않다.
이번엔 $T_i$ 값이 위처럼 상수로 저장하는 것이 아닌 일차 다항식의 계수와 상수를 저장하게 된다고 생각하자.
$f(i)=\displaystyle\sum_{i=0}^i a_i=\alpha_i\cdot i+\beta_i$ 라고 해보자. $\alpha$ 와 $\beta$ 가 각각 계수, 상수이다.
$[L,\,R]$ 에 $d$ 를 모두 더해준다고 할 때 구간을 세개로 나누어 어떤 일이 일어나는지 보자.
구간은 $[0,\,N-1]$ 로 표현되는 $0-based$ 로 생각하자.
1. $[0,\,L-1]$
놀랍게도(?) 아무일도 일어나지 않는다.
2. $[L,\,R]$
$L \le K \le R$ 를 만족하는 $K$ 가 있다고 했을 때, $\alpha_K$ 와 $\beta_K$ 가 얼만큼 변화되는지 알아보자.
$f(i)=\displaystyle\sum_{i=0}^i a_i$ 이므로 $[L,\,K]$ 구간의 변화에 대해서만 이 구간합이 영향을 받게되는데, 모두 $d$ 씩 증가했으므로 총 증가량은 $d \cdot (K-L+1)$ 이고 이를 $K$ 에 대한 일차식으로 다시쓰면 $d\cdot K+(-L+1)d$ 만큼이 변화된다.
따라서 $\alpha_K$ 는 $d$ 만큼, $\beta_K$ 는 $(-L+1)d$ 만큼 더해지면 된다.
여기서 “$f(K)=\alpha_K\cdot K+\beta_K$ 는 그냥 $\beta_K$ 에 $d \cdot (K-L+1)$ 더하면 되는거 아닌가?” 할 수도 있는데, 우리가 만들어야 하는 꼴은 $[L,\,R]$ 에 있는 모든 $K$ 에 대해서 $\alpha$ 와 $\beta$ 에 모두 일관된 값을 증가시키는 식을 찾고싶어하는 것이므로 $K$에 대한 일차 다항식으로 나타내야 한다.
3. $[R+1,\,N-1]$
이곳에 속한 $i$ 들은 $\beta_i$ 만 $(R-L+1) \cdot d$ 만큼 증가하게된다.
왜냐면 영향을 받은 구간의 길이가 $R-L+1$ 이고 모두 $d$ 씩 증가했기 때문이다.
구현 - 업데이트
우린 어쨌든 $f(i)$ 란 1차 다항식을 관리해야 하기 때문에 두 개의 펜윅 트리를 관리해야 한다.
이를 $\alpha,~\beta$ 라고 하자.
1, 2, 3을 종합적으로 생각했을 때 다시 돌아와서 $[L,\,R]$ 구간에 $d$ 를 모두 더해주는 연산에 있어서 값을 어떻게 업데이트해주어야 할까?
일단 $\alpha$ 는 $\alpha_L$ 에 $d$ 를 더해주고 $\alpha_{R+1}$ 에 $d$ 를 빼주면 될 것이다.
2번을 보았을 때 $\beta$ 는 $\beta_L$ 에 $(-L+1)d$ 만큼 증가시켜주고 $\beta_{R+1}$ 에 $(-L+1)d$ 만큼 빼주면 된다.
3번을 보았을 때 $\beta$ 는 $\beta_{R+1}$ 에 $(R-L+1)d$ 만큼 증가시켜주면 된다.
결국 $\beta_{R+1}$ 에서는 $R \cdot d$ 만큼만 증가시켜주면 된다.
구현 - 쿼리
$[L,\,R]$ 의 구간합은 $f(R)-f(L-1)$ 이므로 쉽게 구해줄 수 있다. 결국
$(\alpha_R \cdot R+\beta_R)-(\alpha_{L-1} \cdot (L-1)+\beta_{L-1})$ 임이 보여진다.
결국 업데이트와 쿼리 모두 시간복잡도는 $O(\log N)$ 임이 보인다.
구현 - 코드
식의 유도과정이 순탄치 않았을 뿐이지 코드는 기본 펜윅 트리 두 개를 이용해서 위 식을 표현해주기만 하면 된다.
다음은 그 코드이다.
template<class T>
struct fenwick {
...
};
template<class T>
struct fenwick_range {
int N;
fenwick<T> A, B;
fenwick_range(int N) : N(N), A(fenwick<T>(N + 1)), B(fenwick<T>(N + 1)) {}
void update(int L, int R, int d) {
A.update(L, d);
A.update(R + 1, -d);
B.update(L, (-L + 1) * d);
B.update(R + 1, R * d);
}
T query(int L, int R) {
int R_Value = A.query(0, R) * R + B.query(0, R);
int L_Value = 0;
if (L > 0) {
L_Value = A.query(0, L - 1) * (L - 1) + B.query(0, L - 1);
}
return R_Value - L_Value;
}
};
연습 문제
유명한 Lazy propagation Segment tree 기본 문제이지만, 펜윅 트리로도 풀 수 있다.
Usage 4 - 2차원에서의 펜윅 트리 (Bonus)
펜윅 트리의 특징을 $N$차원에도 그대로 적용시킬 수 있다.
2차원 이라면
BOJ 11658 - 구간 합 구하기 3 문제가 있는데,
보통 2차원 구간합 배열을 써야되는 문제는 값에 업데이트가 없는 문제임과 달리 값에 업데이트가 있다면 2차원 펜윅 트리를 쓸 수 있다.
| 1 | 1 | 1 | 1 |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
과 같이 생긴 배열이 있다면, 2차원 펜윅 트리를 구축할 때 먼저 $x$ 방향으로 훑는다고 해보면 $T_{r,\,c}$ 는 다음과 같이 채워진다.
| 1 | 2 | 1 | 4 |
|---|---|---|---|
| 1 | 2 | 1 | 4 |
| 1 | 2 | 1 | 4 |
| 1 | 2 | 1 | 4 |
이제 $y$ 방향으로 훑으면 다음과 같이 된다.
| 1 | 2 | 1 | 4 |
|---|---|---|---|
| 2 | 4 | 2 | 8 |
| 1 | 2 | 1 | 4 |
| 4 | 8 | 4 | 16 |
이제 $(1, 1)$ 과 $(y, x)$ 영역의 구간합을 구한다고 해보자.
이 구간합을 구할 수 있다면, 2차원 구간합 배열과 동일하게
$\quad \displaystyle \sum_{y=y_1}^{y_2}\sum_{x=x_1}^{x_2} T_{y,\,x}= \\ \qquad \displaystyle \sum_{y=1}^{y_2}\sum_{x=1}^{x_2} T_{y,\,x}-\displaystyle \sum_{y=1}^{y_1-1}\sum_{x=x_1}^{x_2} T_{y,\,x}-\\ \qquad \displaystyle \sum_{y=y_1}^{y_2}\sum_{x=1}^{x_1-1} T_{y,\,x}+ \displaystyle \sum_{y=1}^{y_1-1}\sum_{x=1}^{x_1-1} T_{y,\,x}$
이 성립하기 때문이다.
그럼 우선 $y$ 에 대해서 바깥쪽 loop와 $x$ 에 대해서 안쪽 loop를 구성시켜 쿼리를 수행할 수 있는데, 이 때, $y$ 도 $O(\log Y)$ 만큼 걸리고, $x$ 도 $O(\log X)$ 만큼 걸려서, 시간복잡도는 대략 $O(\log^2 N)$ 정도가 된다.
업데이트는 설명을 생략하고 코드로 대체한다.
다음은 2차원 펜윅 트리의 코드이다.
class fenwick_2d {
public:
int Y, X;
vvi tree;
fenwick_2d(int Y, int X) : Y(Y), X(X) {
tree.resize(Y, vi(X));
}
void update(int y, int x, int diff) {
while (y <= Y) {
int _x = x;
while (_x <= X) {
tree[y][_x] += diff;
_x += _x & -_x;
}
y += y & -y;
}
}
int sum(int y, int x) {
if (y <= 0 || x <= 0) return 0;
int ret = 0;
while (y) {
int _x = x;
while (_x) {
ret += tree[y][_x];
_x -= _x & -_x;
}
y -= y & -y;
}
return ret;
}
int query(int y1, int x1, int y2, int x2) {
return sum(y2, x2) - sum(y1 - 1, x2) - sum(y2, x1 - 1) + sum(y1 - 1, x1 - 1);
}
};



Comments