Heavy Light Decomposition

Prerequisite

• Euler Tour Technic
• Segment Tree or Fenwick Tree

Heavy Light Decomposition

Heavy Light Decomposition 알고리즘은 말 그대로 트리를 무거운 간선과 가벼운 간선으로 나눈다.

HLD라고 명칭한다.

무거운 간선의 정의는, 어떤 노드 $u$에서 자식 노드들 $c_1, \cdots c_k$ 들을 볼 때, 가장 서브트리에 있는 노드들의 개수가 큰 자식으로 이어지는 간선이 무거운 간선이다.

무거운 간선의 정의는 대개 위와 같지만, 꼭 저것대로 짜야할 필요는 없다.

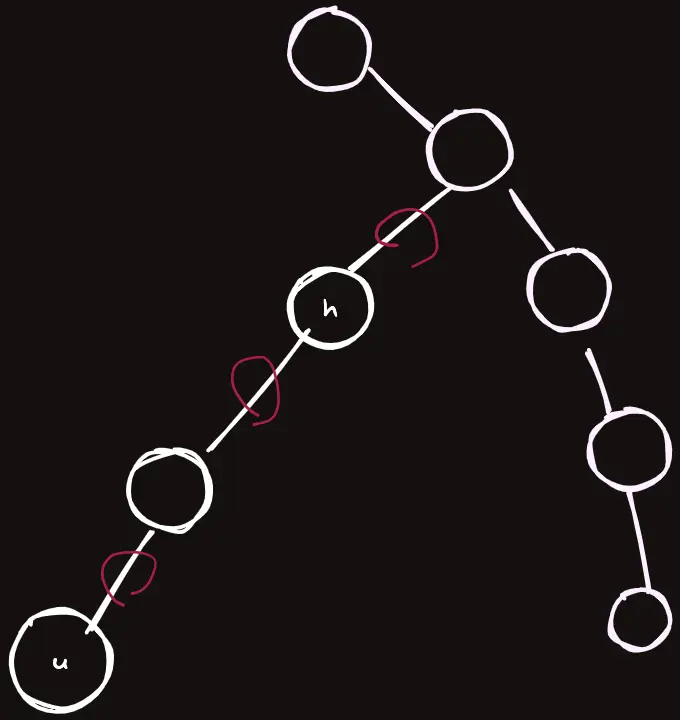
HLD를 나타내는 트리는 다음과 같다.

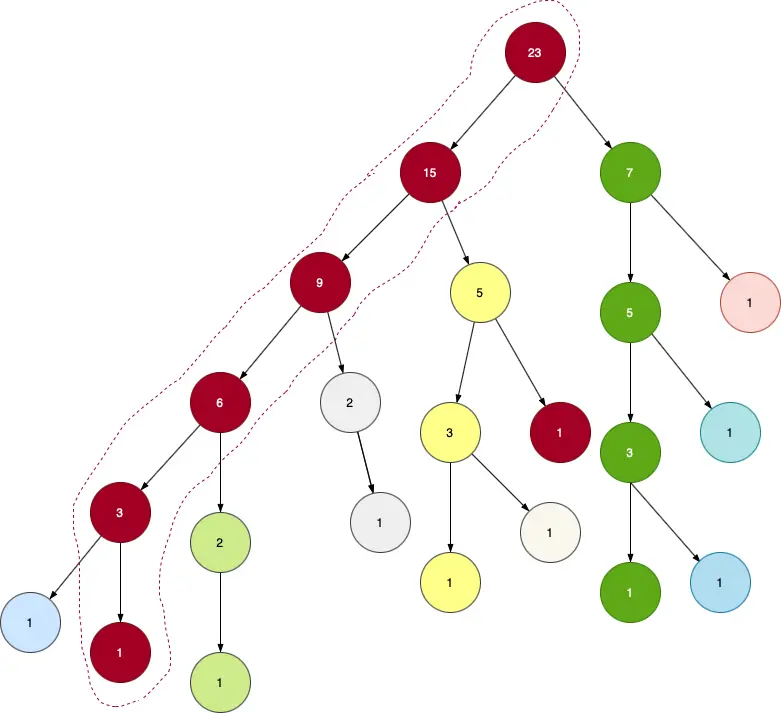
같은 색으로 칠해진 정점을 따라가는 간선들을 보자.

저것들이 바로 무거운 간선이다.

활용

사실 HLD는 어떠한 문제를 풀기 위한 알고리즘이 아닌 그냥 말 그대로 정말 트리의 간선들을 그룹핑하는 테크닉이라고 볼 수 있다.

하지만 이 그룹핑하는 방식이 다른 알고리즘과 같이 쓰기에 굉장히 효율적이기 때문에 HLD는 그러한 알고리즘을 포함하고 있다고 여겨지기도 한다.

그래서 이렇게 간선들을 분리를 해서 무얼 할 수 있을까?

기본적으로 트리 안에 존재하는 정점 $u$와 $v$의 경로에 있는 정점들에 대해서 빠른 쿼리를 날릴 수 있다.

LCA 같은 경우는, 두 정점간의 거리나 간선의 가중치의 합 등 업데이트가 일어나지 않는 쿼리들에 대해서는 쓸만하지만,

HLD를 이용하면 간선들에게 업데이트나 우리가 일반적인 배열 자료구조에서 쓸 수 있는 테크닉들을 마구잡이로 사용해버릴 수 있다.

그냥 정말 세그먼트 트리에 관련된 모든 연산을 트리에서 쓸 수 있게 된다고 이해하면 쉽다.

또한, LCA도 사기적으로 간단하게 구할 수 있다.

int lca(int a, int b) {  
   for (; head[a] ^ head[b]; a = par[head[a]])  
      if (depth[head[a]] < depth[head[b]]) swap(a, b);  
   return depth[a] < depth[b] ? a : b;  
}

원리

위와 같이 HLD를 적용시켜놨다고 하자. 쿼리를 날리는 원리는 심플하다.

1. Euler Tour Technic으로 트리를 펴놓는다.
2. 정점 $u, v$에 대해서 $u$와 $v$의 경로에 어떠한 연산을 가해주고 싶다면, $u$와 $v$의 경로에 있는 모든 그룹에 대해서 그 연산들을 모두 해준다.
   1. 예를 들어, 구간합 연산이라면 그 그룹들에 있는 값들을 모두 더해주면 될 것이고, 구간 업데이트 연산이라면 펴진 트리에 Lazy Propagation Segment Tree 같은걸 끼얹어서 연산을 해주면 된다.
3. Done!

시간복잡도

일단, HLD 구성에 대한 시간복잡도를 보자.

HLD는 두 번의 DFS만으로 위와 같이 트리를 분리할 수 있는데, 따라서 $O(N)$으로 구성이 된다.

쿼리에 대한 시간복잡도는 조금 생각해볼만 하다.

사실 위에서 쿼리를 날리는 방법에는 심각한 결함이 있는 것 같다.

$u$와 $v$의 경로에 있는 모든 그룹에 대해서 연산을 적용해준다고 했는데, 그 그룹들이 몇개가 될 줄 알고 그렇게 쿼리를 수행할 수 있단 말인가?

결론적으로 그 그룹들의 개수는 $O(\log N)$ 로 제한된다.

현재 그룹에서 다른 그룹으로 넘어가는 상황을 보자.

일반성을 잃지않고 현재 무거운 간선에서 가벼운 간선으로 넘어간다고 하자.

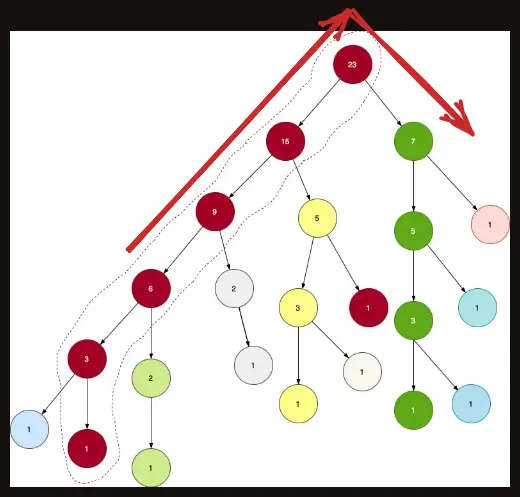
그 행위는 곧 $k$의 서브트리의 크기의 절반 이상의 정점을 건너뛰는 것이 된다.

$k$의 서브트리의 크기가 $S$ 라고 할 때 $c_h$ 가 가장 무거운 자식이라고 할 때, $c_h$ 의 크기가 $c_h>\dfrac S2$ 라면 당연히 절반 이상을 건너 뛴 것이고, $c_h \le \dfrac S2$ 라면 현재 이동하는 가벼운 간선쪽 그룹의 서브트리의 크기가 $c_l$ 이라면 $c_l \le c_h$ 이기 때문에 $S-c_l \left(\ge \dfrac S2\right)$ 개의 정점을 건너뛴 것이기 때문이다.

따라서 $u \to v$ 의 경로에는 최대 $O(\log N)$ 개의 그룹이 있고, 구현상 그룹의 $head$를 $O(1)$에 얻어올 수 있기 때문에 경로에 존재하는 모든 그룹을 순회하는데는 $O(\log N)$ 이 걸린다.

여기에 세그먼트 트리같은 자료구조의 연산을 끼얹으면 쿼리는 대략 $O(\log^2 N)$ 정도 걸린다고 볼 수 있다.

정점연산과 간선연산

앞선 내용들에서 그룹에 관련해서 정점과 간선을 구분지어 설명하지 않은 이유가 있는데, HLD에서는 잘 구현하면 정점과 간선 모두에 위에서 언급한 연산들을 적용해 줄 수 있기 때문이다.

즉, 정점에 가중치가 있는 연산 혹은 간선에 가중치가 있는 연산 모두 구현법에 따라 커버할 수 있다.

밑에서 자세히 알아볼 것이다.

구현

HLD의 구현은 짧지 않은 편에 속하고, 구현법이 조금씩 상이할 수 있다.

다음과 같은 문제를 해결해보면서 구현을 해보도록 하자.

BOJ 13510 - 트리와 쿼리 1 연습문제부터 플레티넘 1이 찍혀있지만, HLD를 쓰면 쉽게 풀린다.

• 1 i c: i번 간선의 비용을 c로 바꾼다.
• 2 u v: u에서 v로 가는 단순 경로에 존재하는 비용 중에서 가장 큰 것을 출력한다.

딱 우리가 HLD를 써서 해결하려는 문제와 동일하다.

일단, 초기화 과정부터 보자.

초기화

구조체를 만들고, 생성자 등 간선을 입력받는 작업부터 하자.

struct Edge {  
   int to, cost;  
};  
  
struct HLD {  
   int N;  
   vector<vector<Edge>> edges;  
   HLD(int N) : N(N) {  
      edges.resize(N);  
   }  
  
   void add_edge(int u, int v, int w) {  
      edges[u].push_back({v, w});  
      edges[v].push_back({u, w});  
   }  
  
   void init(int root = 0) {  
  
   }  
};

간선은 꼭 양방향으로 모두 추가해주자.

DFS 1

첫 번째 DFS는 서브트리들의 크기를 구성하고 가장 큰 서브트리를 가진 자식이 간선 배열의 $0$ 번째에 위치하도록 한다.

depth 배열도 채워준다. 쿼리에 필요하다.

void dfs1(int cur, int p) {  
   subtree_size[cur] = 1;  
   head[cur] = cur;  
  
   for (int i = 0; i < sz(edges[cur]); i++) {  
      Edge &e = edges[cur][i];  
      if (e.to == p) continue;  
      depth[e.to] = depth[cur] + 1;  
      dfs1(e.to, cur);  
  
      // swap if greatest subtree size is detected
      if (edges[cur][0].to == parent[cur] || subtree_size[e.to] > subtree_size[edges[cur][0].to])  
         swap(edges[cur][0], edges[cur][i]);  
  
      subtree_size[cur] += subtree_size[e.to];  
   }  
}

이 때, 부모가 0번째 오지않도록 방지하는 것은 스킵해도 된다. 그러면 설명한대로 HLD가 만들어지지 않고 안 끊겨도 될 그룹이 끊기겠지만, 문제를 푸는데 지장이 있을만한 시간복잡도 손실은 아니다.

DFS 2

void dfs2(int cur, int p) {  
   in[cur] = dfsn++;  
  
   for (int i = 0; i < sz(edges[cur]); i++) {  
      Edge &e = edges[cur][i];  
      if (e.to == p) continue;  
      head[e.to] = i == 0 ? head[cur] : e.to;  
      dfs2(e.to, cur);  
   }  
}

DFS 2에서는 Euler Tour Technic에 필요한 in 배열을 채워준다.

어떤 정점이 트리를 폈을 때 방문 횟수가 몇번인지 (DFS number) 기록해두는 것이다.

DFS1이 아닌 꼭 DFS2에서 in 배열을 채워줘야하는 이유는 DFS1은 자식들간의 서브트리 크기에 따라 재배치가 일어나고 있는 시점이고, 재배치가 일어난 다음엔 항상 $0$번 자식이 무거운 간선이 되기 때문에 DFS2 에서 순서대로 in 을 채우면 되기 때문이다.

또한, head 라는 배열도 채우는데, 각 정점당 자신이 속해있는 그룹에서 가장 위에 위치한 그룹의 머리를 기록해두는 것이다.

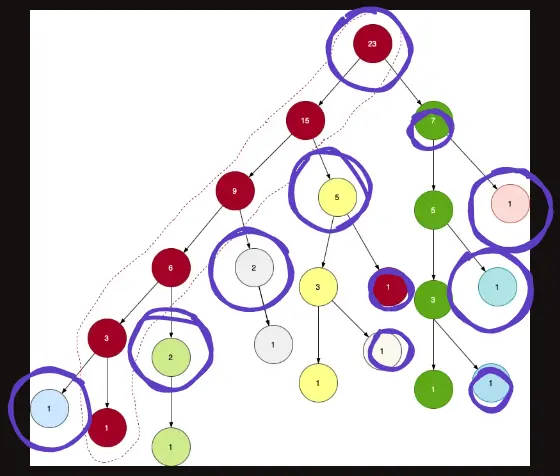
사진에서 보라색 동그라미가 있는 것들이 각각 그룹의 head를 나타낸다.

간선의 가중치 할당

이제 Euler Tour Technic에 이용할 수 있는 간선들의 in 번호가 준비되었으므로, 처음에 입력받은 간선들에서 간선의 가중치를 세그먼트 트리에 업데이트 할 것이다.

일단 세그먼트 트리를 하나 준비해준다.

다음과 같이 업데이트 해준다.

for (int i = 0; i < N; i++) {  
   for (Edge &e: edges[i]) {  
      if (parent[e.to] == i) {  
         seg.update(in[e.to], e.cost);  
      }  
   }  
}

현재 이 구현체에서 HLD의 in 정점 번호에서 저장하고 있는 값은 자신의 부모로 가는 간선에 대한 가중치이다.

HLD를 구현함에 있어서 위처럼 “간선은 ~ 같이 처리하겠다” 라는 자신만의 명확한 기준을 가지고 구현을 하는것을 추천한다.

우리는 트리에 간선을 추가할 때 양방향으로 추가했으므로 두 번 값이 중복되어서 계산되지 않게끔 $u, v$가 있고 $u$가 $v$의 부모 노드라면, $in[v]$ 의 값에 처음에 받은 $cost$를 업데이트 해주면 된다.

이제 초기화 함수의 작성이 끝났다.

void init(int root = 0) {  
   dfs1(root, -1);  
   dfs2(root, -1);  
   for (int i = 0; i < N; i++) {  
      for (Edge &e: edges[i]) {  
         if (parent[e.to] == i) {  
            seg.update(in[e.to], e.cost);  
         }  
      }  
   }  
}

간선 가중치 업데이트 쿼리

• 1 i c: i번 간선의 비용을 c로 바꾼다.

이런 쿼리를 처리하기 위해 일단 $i$번 간선이 뭔지를 알아야하고 $i$번 간선은 $u, v, w$ 라는 정보를 갖고 있을 것이다. ($u, v$ 는 정점 번호이고 $w$ 는 가중치이다.)

일반성을 잃지 않고 $u$가 $v$의 부모라면, $in[v]$ 의 가중치를 업데이트 해주면 된다.

// HLD 구조체 내부
void update(int u, int v, int c) {  
   if (parent[u] == v) swap(u, v);  
   assert(parent[v] == u);  
  
   fenw.update(in[v], c);  
}

간선 가중치 구간 최대값 쿼리

이제 여기서부터 진짜 HLD의 그룹을 이용하게 된다.

앞서 말했듯이, 이 쿼리의 시간복잡도는 $O(\log ^2 N)$ 이다.

다음과 같은 알고리즘을 수행한다.

• $u$와 $v$가 다른 그룹에 속했다면 (head 가 다름으로 판단), 각각의 그룹의 head중 더 트리에서 깊게 있는 것을 한 그룹 위로 올려준다.
  • 올려주며, 해당 그룹의 간선들에서의 MAX 값을 정답에 연산한다.
  • 이제 그 다음 간선은 그룹의 head의 부모가 되어야 하므로 parent[head[u]] 가 된다.
• 같은 그룹에 속했다면, 이제 그 두개에 대해서 쿼리를 하고 종료한다.

int query(int u, int v) {  
   int ret = 0;  
  
   while (head[u] ^ head[v]) {  
      // u의 head가 v의 헤드보다 더 트리 깊은곳에 있게 만든다.  
      if (depth[head[u]] < depth[head[v]]) swap(u, v);  
  
      ret = max(ret, seg.query(in[head[u]], in[u]).max);  
      u = parent[head[u]];  
   }  
  
   // u가 더 트리 깊은곳에 있게 만든다.  
   if (depth[u] < depth[v]) swap(u, v);  
   ret = max(ret, seg.query(in[v] + 1, in[u]).max);  
  
   return ret;  
}

코드를 잘 보자. 마지막 쿼리에 in[v] 에 더해지는 1은뭘까?

아까 필자의 코드에선 in[v] 가 가리키는 값은 v 정점에서 parent[v] 정점으로 이어지는 간선의 가중치를 의미하게 된다고 했다.

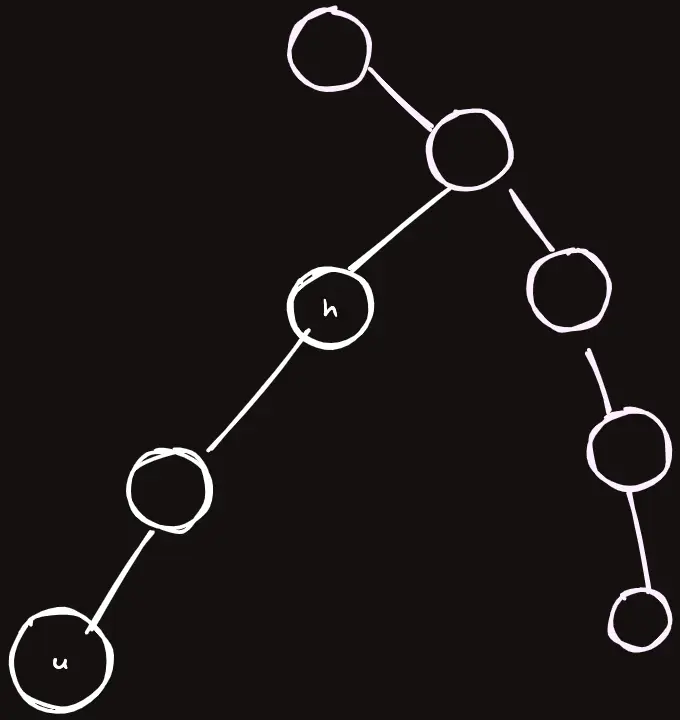
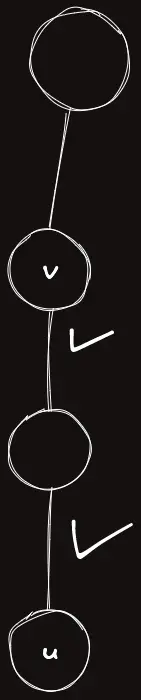
와 같은 상황에서, $u$ 에서 같은 그룹에 있는 모든 간선들에서 연산을 해주어야 한다고 하자. 다음과 같은 간선들이다.

그러면 seg.query(in[head[u]], in[u]) 라는 구간이 왜 나왔는지 이해가 될 것이다.

head[u] 에서 parent[head[u]] 로 가는 간선도 연산에 포함시켜주어야 하기 때문이다.

그러나 이제 같은 그룹에 있고 다음과 같은 상황이라고 하자.

seg.query(in[head[u]], in[u]) 이 코드를 그대로 써줄 수 있을까?

in[head[u]] 를 포함해버리면 $v$ 에서 그 위로 가는 간선까지 연산에 포함시켜버리겠다는 뜻이다.

따라서 연산의 범위에 $+1$ 을 해서 올바른 구간에 대한 쿼리를 수행할 수 있다.

여기서 만약 연산의 주체가 간선이 아닌 정점이라면, $+1$ 을 해주지 않아도 된다. 따라서 연산의 주체가 정점인지 간선인지는 바로 이 부분에서 결정이 난다!

Template

필자는 HLD를 템플릿으로 만들어두었다.

Lazy Propagation Segment Tree + HLD 템플릿이다.

template<class T>  
struct seg_lazy {  
private:  
   const T INF = numeric_limits<T>::max() >> 1;  
   struct node {  
      T sum = 0, min = 0, max = 0, lazy = 0;  
      node(T v) : sum(v), min(v), max(v) {}  
      node(T sum, T min, T max) : sum(sum), min(min), max(max) {}  
   };  
   const node identity{0, INF, -INF};  
   int N;  
   vector<node> tree;  
   node merge(node l, node r) {  
      node ret = {l.sum + r.sum, min(l.min, r.min), max(l.max, r.max)};  
      return ret;  
   }  
   void propagate(int n, int nl, int nr) {  
      if (!tree[n].lazy) return;  
      tree[n].sum += (nr - nl + 1) * tree[n].lazy;  
      tree[n].max += tree[n].lazy;  
      tree[n].min += tree[n].lazy;  
      if (nl != nr) {  
         tree[n * 2].lazy += tree[n].lazy;  
         tree[n * 2 + 1].lazy += tree[n].lazy;  
      }  
      tree[n].lazy = 0;  
   }  
   void update(int n, int nl, int nr, int l, int r, T v) {  
      propagate(n, nl, nr);  
      if (nl > r || nr < l) return;  
      if (nl >= l && nr <= r) {  
         tree[n].lazy += v;  
         propagate(n, nl, nr);  
         return;  
      }  
      int m = (nl + nr) >> 1;  
      update(n * 2, nl, m, l, r, v);  
      update(n * 2 + 1, m + 1, nr, l, r, v);  
      tree[n] = merge(tree[n * 2], tree[n * 2 + 1]);  
   }  
   node query(int n, int nl, int nr, int l, int r) {  
      propagate(n, nl, nr);  
      if (nl > r || nr < l) return identity;  
      if (nl >= l && nr <= r) return tree[n];  
      int m = (nl + nr) >> 1;  
      return merge(query(n * 2, nl, m, l, r), query(n * 2 + 1, m + 1, nr, l, r));  
   }  
public:  
   seg_lazy(int N) : N(N) {  
      int tree_size = 1 << ((int) ceil(log2(N)) + 1);  
      tree = vector<node>(tree_size, node(0));  
   }  
   void update(int l, int r, T v) { update(1, 0, N - 1, l, r, v); }  
   node query(int l, int r) { return query(1, 0, N - 1, l, r); };  
};  
  
template<class T>  
struct HLD {  
   struct Edge { T to, cost; };  
   int N, next_dfsn = 0, for_edge, any_cost = 0;  
   vi subsize, par, depth, head, in, out;  
   vector<vector<Edge>> edges;  
   seg_lazy <T> seg;  
   HLD(int N, int for_edge = 1)  
      : N(N), for_edge(for_edge), par(N), subsize(N), depth(N), edges(N), head(N), in(N), out(N),  
        seg(seg_lazy<T>(N)) {}  
   void add_edge(int u, int v, T cost = 0) {  
      edges[u].pb({v, cost});  
      if (cost)any_cost = 1;  
   }  
   void init(int root = 0) {  
      dfs1(root, -1);  
      dfs2(root, -1);  
      for (int cur = 0; cur < N && any_cost; cur++)  
         for (const Edge &e: edges[cur])  
            if (par[e.to] == cur)  
               update_node(e.to, e.cost);  
   }  
   void dfs1(int cur, int p) {  
      subsize[cur] = 1;  
      for (Edge &e: edges[cur]) {  
         if (e.to == p) continue;  
         depth[e.to] = depth[cur] + 1;  
         dfs1(e.to, cur);  
         subsize[cur] += subsize[e.to];  
         if (subsize[e.to] > subsize[edges[cur][0].to])swap(edges[cur][0], e);  
      }  
   }  
   void dfs2(int cur, int p) {  
      par[cur] = p;  
      in[cur] = next_dfsn++;  
      for (const Edge &e: edges[cur]) {  
         if (e.to == par[cur]) continue;  
         head[e.to] = (e.to == edges[cur][0].to) ? head[cur] : e.to;  
         dfs2(e.to, cur);  
      }  
      out[cur] = next_dfsn - 1;  
   }  
   void update_node(int i, T v) { seg.update(in[i], in[i], v); }  
   void update_path(int a, int b, T v) {  
      for (; head[a] ^ head[b]; a = par[head[a]]) {  
         if (depth[head[a]] < depth[head[b]]) swap(a, b);  
         seg.update(in[head[a]], in[a], v);  
      }  
      if (depth[a] > depth[b]) swap(a, b);  
      seg.update(in[a] + for_edge, in[b], v);  
   }  
   T query_sum(int a, int b) {  
      if (a == b) return seg.query(in[a], in[a]).sum;  
      T ret = 0;  
      for (; head[a] ^ head[b]; a = par[head[a]]) {  
         if (depth[head[a]] < depth[head[b]]) swap(a, b);  
         ret += seg.query(in[head[a]], in[a]).sum;  
      }  
      if (depth[a] > depth[b]) swap(a, b);  
      return ret + seg.query(in[a] + for_edge, in[b]).sum;  
   }  
   T query_max(int a, int b) {  
      if (a == b) return seg.query(in[a], in[a]).max;  
      T ret = -seg.INF;  
      for (; head[a] ^ head[b]; a = par[head[a]]) {  
         if (depth[head[a]] < depth[head[b]]) swap(a, b);  
         ret = max(ret, seg.query(in[head[a]], in[a]).max);  
      }  
      if (depth[a] > depth[b]) swap(a, b);  
      return ret = max(ret, seg.query(in[a] + for_edge, in[b]).max);  
   }  
   T query_min(int a, int b) {  
      if (a == b) return seg.query(in[a], in[a]).min;  
      T ret = seg.INF;  
      for (; head[a] ^ head[b]; a = par[head[a]]) {  
         if (depth[head[a]] < depth[head[b]]) swap(a, b);  
         ret = min(ret, seg.query(in[head[a]], in[a]).min);  
      }  
      if (depth[a] > depth[b]) swap(a, b);  
      return ret = min(ret, seg.query(in[a] + for_edge, in[b]).min);  
   }  
   int lca(int a, int b) {  
      for (; head[a] ^ head[b]; a = par[head[a]])  
         if (depth[head[a]] < depth[head[b]]) swap(a, b);  
      return depth[a] < depth[b] ? a : b;  
   }  
};