Euler Tour Technic + $O(1)$ LCA

Prerequisite

• 문제에 Segment Tree or Fenwick Tree 가 쓰임

Euler tour technic

오일러 투어 테크닉은 트리를 배열처럼 일자로 필 수 있는 테크닉이다.

이것만으로 풀 수 있는 문제는 몇 개 없지만, Heavy-Light-Decomposition 같은 더 고급 알고리즘의 구현에 쓰이거나 세그먼트 트리 등과 활용하여 트리의 특정 서브트리에 일정한 연산을 수행시키는 등 쓸 데가 무궁무진하다.

구현

구현도 아주 간단하다.

DFS를 한 번만 수행하면서 각 노드가 DFS 순회에서 방문되는 순서를 기록해두면 된다.

다음과 같은 트리를 보자.

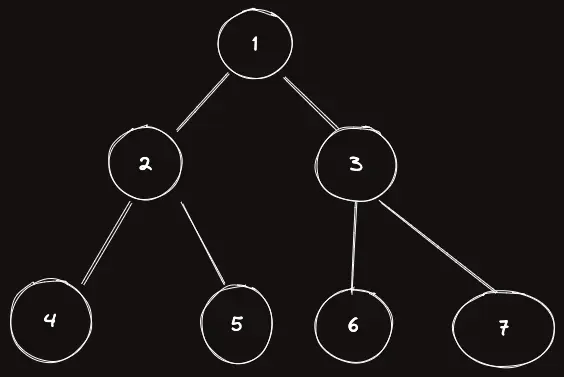
이제 이 트리에서 DFS 방문 순서대로 번호를 매겨보자. 이를 in[i] 라고 하자.

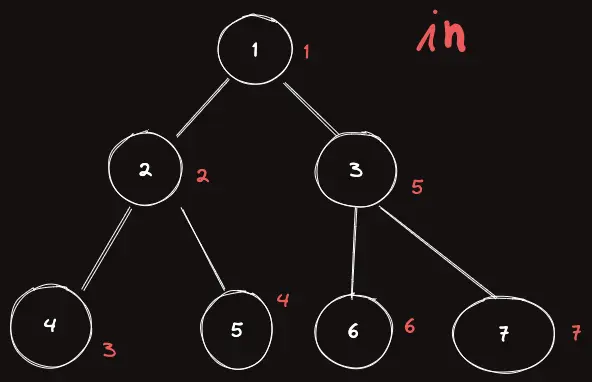
이걸 코드로 나타내면 다음과 같다.

int dfsn = 0;

void dfs(int i) {
   in[i] = dfsn++;
   for (int child: edges[i]) {
      dfs(child);
   }
}

여기서 이제 DFS 를 순회하다가 해당 정점을 탈출할 때의 dfsn 를 out[i] 라고 하자.

그럼 out[i] 는 다음과 같다.

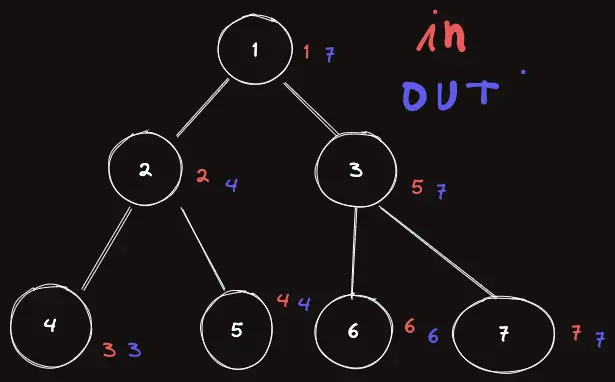
다시 코드에 나타내보자. 제일 마지막 줄에 추가해주면 된다.

void dfs(int i) {
   in[i] = dfsn++;
   for (int child: edges[i]) {
      dfs(child);
   }
   out[i] = dfsn - 1; // here
}

이렇게 만들어서 in, out 을 어디에 쓸까?

우리가 루트 노드를 3 번 노드로 하는 서브 트리에 모두 1씩 더해주고 싶다고 하자.

놀랍게도 in[3] ~ out[3] 까지가 바로 그 서브트리에 존재하는 노드들임을 알 수 있다.

여기에서 인덱스는 적절히 관리를 해주어야 한다. 3번 노드지만 실제로 서브트리에 있는 in 값들은 5, 6, 7 이기 때문이다. 보통 $k$ 번 노드에 대한 어떤 연산을 요구한다면 $\mathrm{in}_k$ 를 갖고 그 연산을 수행해주면 된다.

트리에서 DFS 순서로 다시 인덱스가 매핑되었다고 생각할 수 있다.

연습 문제

BOJ 2820 - 자동차 공장

이 문제는 쿼리를 보면 range update와 point query를 요구하므로 Lazy propagation Segment tree 나 Fenwick tree 를 쓰면 해결된다.

다만, 이 문제에서는 자기 자신을 제외한 서브트리의 노드들만 업데이트를 해주어야 하므로 in[k] + 1 ~ out[k] 까지만 업데이트 해주는 것만 유의한다.

int n, m;
vi a, par, in, out;
vvi edges;

int dfsn = 0;

void dfs(int i) {
   in[i] = dfsn++;
   for (int child: edges[i]) {
      dfs(child);
   }
   out[i] = dfsn - 1;
}

void solve() {
   cin >> n >> m;
   a.resize(n);
   edges.resize(n);
   in.resize(n);
   out.resize(n);

   for (int i = 0; i < n; i++) {
      int x, p;
      cin >> x;
      if (i) cin >> p;
      a[i] = x;
      if (i)
         edges[p - 1].pb(i);
   }

   dfs(0);
   fenwick_point<int> fw(n);
   for (int i = 0; i < n; i++) {
      fw.update(in[i], in[i], a[i]);
   }

   for (int i = 0; i < m; i++) {
      string cmd;
      cin >> cmd;
      if (cmd == "p") {
         int k, x;
         cin >> k >> x, k--;
         fw.update(in[k] + 1, out[k], x);
      } else {
         int k;
         cin >> k, k--;
         cout << fw.query(in[k]) << endl;
      }
   }
}

BOJ 15491 - 도시 정비

도시를 하나 없앤다는 말은 리프 노드가 아닌 이상 트리를 끊는다는 것을 의미한다.

트리를 끊은 후에 나뉘어진 서브트리들 모두에 대해 해당 서브트리에서 가장 큰 노드값을 알면 된다.

어떤 노드 $k$ 가 제거된다면, $k$ 의 트리에서의 자식들의 서브트리는 앞서 봤듯이 오일러 투어 테크닉을 적용해둔 배열을 가지고 있다면 Range Max Query를 이용해 각각 구해줄 수 있다.

문제는 $k$ 의 부모에 대해서인데, 다음과 같은 좀더 복잡한 트리 그림을 보자.

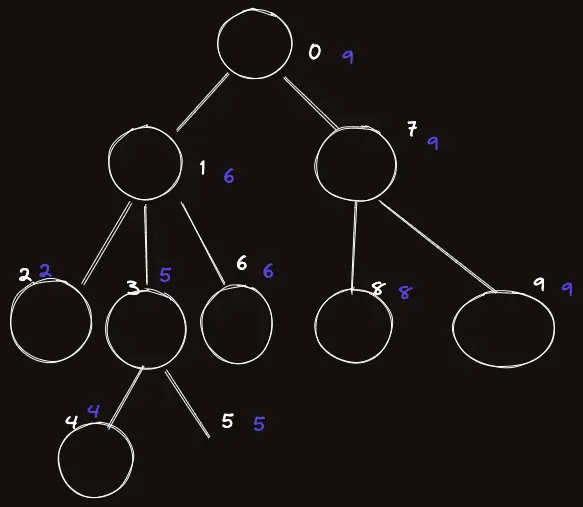
흰색 글씨가 in 이다.

만약 in=3 인 노드의 부모쪽에 대해서 생각해보자.

그러면 0 ~ 3 - 1 까지와 in=3 인 부분의 out 인 5에 대해 5+1 ~ 9 까지 두 부분에서의 Max 값의 Max 가 부모 노드쪽의 Max 가 된다.

구현은 다음과 같다.

이 문제는 업데이트가 필요하지 않기 때문에 그저 RMQ 를 빠르게 구할 수 있다면 충분하다. 따라서 Sparse Table로 $O(1)$ 로 구할 수 있는 구현을 사용하도록 하겠다.

사실 이 문제는 데이터 추가로 데이터가 너무 많아져서 $O(1)$ 로 짜도 빡빡하다.

int LOG = 20;
void solve() {
   int n;
   cin >> n;
   vi arr(n);
   fv(arr);
   vvi edges(n);
   for (int i = 0; i < n - 1; i++) {
      int u, v;
      cin >> u >> v, u--, v--;
      edges[u].pb(v), edges[v].pb(u);
   }

   vi in(n), out(n), par(n, -1);

   int dfsn = 0;
   function<void(int, int)> dfs = [&](int i, int p) -> void {
      par[i] = p;
      in[i] = dfsn++;
      for (int to: edges[i]) if (to != p) dfs(to, i);
      out[i] = dfsn - 1;
   };
   dfs(0, -1);

   vi log2(n + 1, -1);
   for (int i = 1, k = 0; i <= n; i <<= 1, k++) log2[i] = k;
   for (int i = 1; i <= n; i++) if (log2[i] == -1) log2[i] = log2[i - 1];

   vvi sparse(n, vi(LOG, -1));
   for (int i = 0; i < n; i++) sparse[in[i]][0] = arr[i];
   for (int k = 1; k < LOG; k++)
      for (int i = 0; i + (1 << k) - 1 < n; i++) {
         sparse[i][k] = max(sparse[i][k - 1], sparse[i + (1 << (k - 1))][k - 1]);
      }

   auto query = [&](int l, int r) {
      if (l > r) return 0;
      int len = r - l + 1;
      int L = log2[len];
      return max(sparse[l][L], sparse[r - (1 << L) + 1][L]);
   };
   int ans = 0;
   for (int i = 0; i < n; i++) {
      int ret = 0;
      for (int to: edges[i]) {
         if (to == par[i]) continue;
         ret += query(in[to], out[to]);
      }

      if (par[i] != -1)
         ret += max(query(in[0], in[i] - 1), query(out[i] + 1, out[0]));
      ans = max(ans, ret);
   }
   cout << ans;
}

이 코드에서 처음 Sparse table을 초기화 해주는 과정에서 sparse[in[i]][0] = arr[i] 와 같은 친구를 볼 수 있는데,
여기서 인덱스에 유의하자. 밑에서 $i$ 를 순회하는 코드가 $in_i$ 를 이용해 쿼리를 날리므로 테이블의 $in_i$ 번째 인덱스에 $arr_i$ 를 초기화 시켜두는 것이 올바르다.

2n-1 개의 번호가 붙는 Euler Tour Technic

지금은 $in$ 과 $out$ 이 모두 $[0,\,N)$ 의 번호가 붙었는데, 다른 방식으로 ETT(Euler Tour Technic) 을 사용해줄 수도 있다.

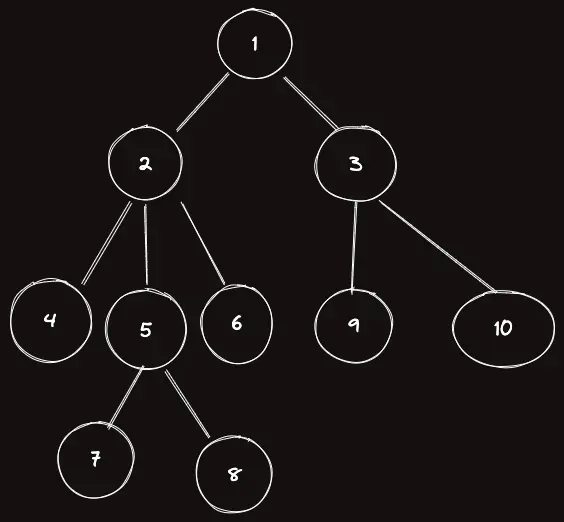
이 트리를 갖고 얘기를 계속해보자.

앞서 ETT를 구성하는 방법이 각 노드가 DFS 순회에서 언제 들어갔다가 나오는지를 저장해두는 것이였다면, 이번에는 DFS 순회에서 $k$ 번째 방문되는 노드가 어떤 노드인지를 저장하는 것에 의미가 있다.

이 방문 순서라는 것은 총 $2n-1$ 개가 나오는데, 테이블을 채워보도록 하자.

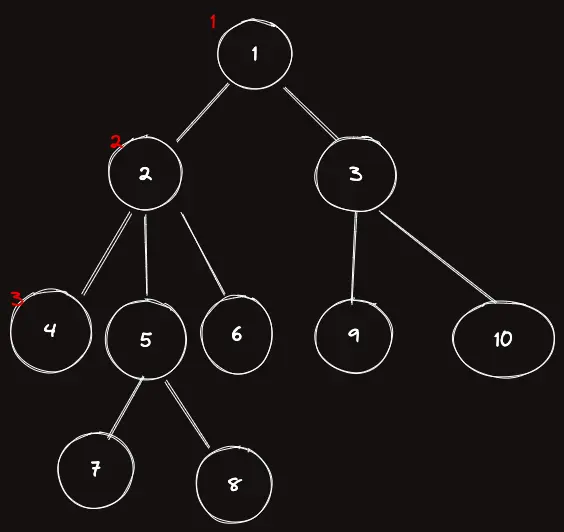
이렇게 방문을 하면, 3까지 채워진다.

$i$	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
$order$	1	2	3

이제 다시 4까지 방문을 마치고 2로 올라가서 7까지 가보자.

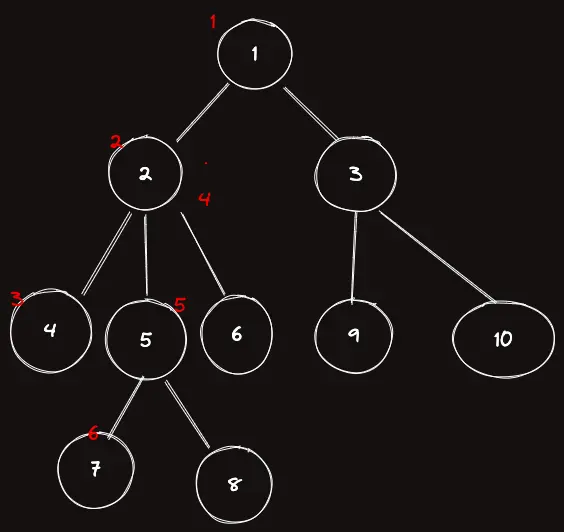
$i$	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
$order$	1	2	3	2	5	7

이제 귀찮으므로 다 채워버리도록 하겠다

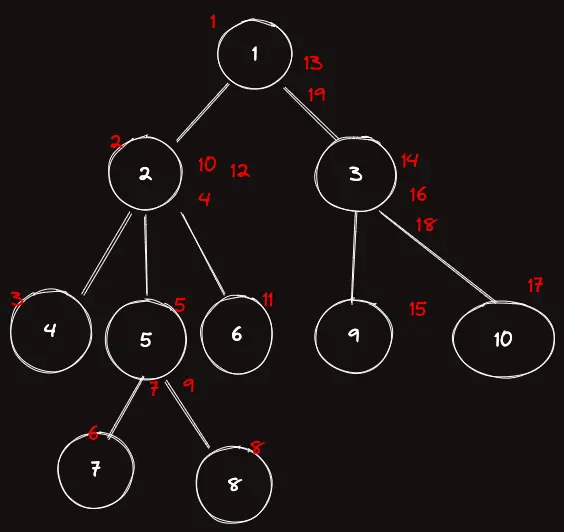
$i$	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
$order$	1	2	3	2	5	7	5	8	5	2	6	2	1	3	9	3	10	3	1

이걸 이제 어떻게 쓸까?

이것이 필요한 예시는 대표적으로 $O(1)$ LCA 가 있다.

$O(1)$ LCA

$O(1)$ 라고 해도 시간적으로 PS에 있어 유의미한 차이를 갖지는 않는다. $2n-1$ 개의 길이를 가진 배열이 필요할 뿐더러 전처리도 오래걸린다.

보통 LCA(Lowest Common Ancestor)라 하면 Sparse table을 적절히 구축한 후에 쿼리당 $O(\log N)$ 시간이 걸리는 것이 기본적인데, 이건 ETT 를 이용해 Level에 대한 Range Minimum Query로 $O(1)$ 만에 쿼리를 때려버리는게 핵심 아이디어이다.

DFS 를 하며 따로 길이 $N$ 의 $in_i$ 도 만들어두었다고 해보자.

단, 여기서 $in$의 값들엔 $0 \sim 2n-1$범위의 값이 들어감에 유의하자.

LCA를 찾으려는 두 노드중 $in$ 이 더 낮은 것을 $u$ 라고 하고 나머지를 $v$ 라고 한다면,$in_u \le i \le in_v$ 고 $order_i=k$를 만족하는 $k$ 중 가장 $level_k$ 이 낮은 $k$ 가 바로 LCA 이다.

위에서 얘기하던 트리를 다시 보자.

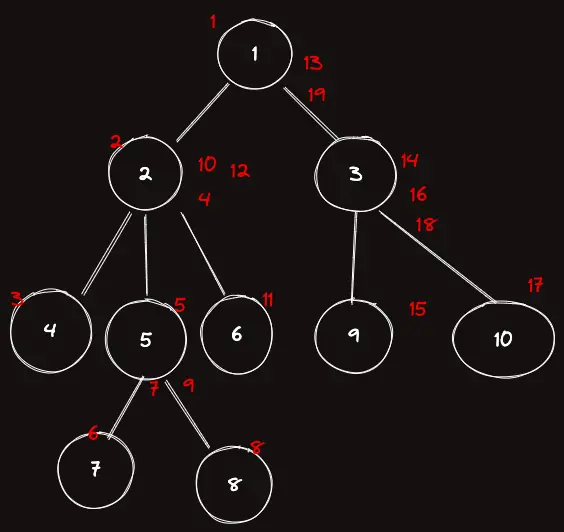
여기서 6과 7의 최소 공통조상(=2) 를 어떻게 찾는지 살펴볼 것이다.

$i$	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
$order$	1	2	3	2	5	7	5	8	5	2	6	2	1	3	9	3	10	3	1

$in_7 < in_6$ 이므로

$i$	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
$order$	1	2	3	2	5	7	5	8	5	2	6	2	1	3	9	3	10	3	1

중에서 가장 낮은 $level$ 을 가진 노드는 $2$ 이므로 6과 7의 LCA는 2임이 보여진다.

그리고 이 $level$ 에 대해 Sparse Table을 이용해 RMQ 를 $O(1)$ 에 처리할 수 있도록 전처리가 되어있다면 $O(1)$ LCA 구현이 완성된다.

구현은 따로 설명하지 않고 코드를 첨부한다.

struct LCA_O1 {
   int N, LOG = 0, dfsn = 0;
   vvi edges;
   vi level, in, e, lg2, pw2;
   vector<vector<pi>> sparse;
   LCA_O1(int N)
      : N(N), level(N), in(N, -1), e(N * 2 - 1), edges(N), lg2(N * 2, -1) {
      for (; (1 << LOG) <= N; LOG++);
      LOG++;
      sparse.resize(N * 2 - 1, vector<pi>(LOG));
      pw2.resize(LOG, 1);
   }
   void add_edge(int i, int j) { edges[i].pb(j); }
   void dfs(int cur, int l) {
      level[cur] = l;
      e[dfsn] = cur;
      in[cur] = dfsn++;
      for (int to: edges[cur]) {
         if (in[to] == -1) {
            dfs(to, l + 1);
            e[dfsn++] = cur;
         }
      }
   }
   void build(int root = 0) {
      for (int i = 1, k = 0; i < N * 2; i <<= 1, k++) lg2[i] = k;
      for (int i = 2; i < N * 2; i++) if (lg2[i] == -1)lg2[i] = lg2[i - 1];
      for (int i = 1; i < LOG; i++) pw2[i] = pw2[i - 1] << 1;
      dfs(root, 0);
      for (int i = 0; i < N * 2 - 1; i++) sparse[i][0] = {level[e[i]], e[i]};
      for (int k = 1; k < LOG; k++) {
         for (int i = 0; i + pw2[k - 1] < N * 2 - 1; i++) {
            int j = i + pw2[k - 1];
            sparse[i][k] = min(sparse[i][k - 1], sparse[j][k - 1]);
         }
      }
   }
   int find(int a, int b) {
      int l = min(in[a], in[b]), r = max(in[a], in[b]), k = lg2[r - l + 1];
      r -= pw2[k] - 1;
      return min(sparse[l][k], sparse[r][k]).se;
   }
   int dist(int a, int b) {
      int l = find(a, b);
      return level[a] + level[b] - level[l] * 2;
   }
};