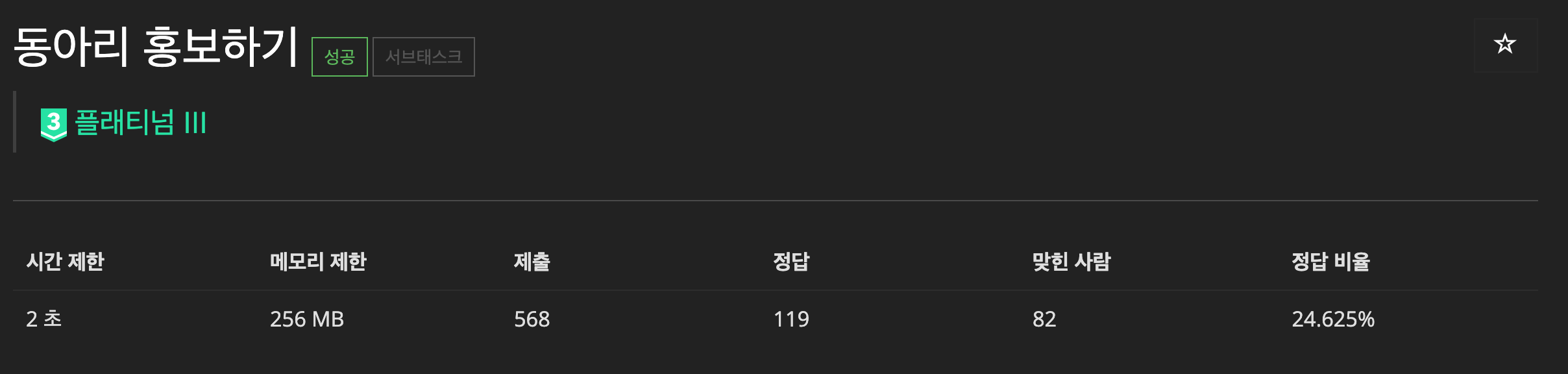
BOJ 17493 - 동아리 홍보하기

BOJ 17493 - 동아리 홍보하기

대개 이런 문제들은 Leaf 노드부터 위상정렬을 이용해 그리디하게 많이 푸는 편인데

이 문제는 Leaf의 부모가 항상 전단지가 붙어야된다 이후로 딱히 생각을 발전시키기 어려워 DP의 상태를 정의해 풀었다.

$dp[i][on_p][on_c]=i$ 에서 부모에 전단지가 붙은 상태 $op_p$ 이고 $i$에 전단지를 붙일건지 말건지가 $op_c$ 일 때 $i$의 서브트리에서 전단지를 붙이는 경우의 수이다.

$i$에 대해 상태는 $3$개만 있어도 되지만 $4$개로 정의했다.

다른 경우는 그냥 자식들에서 적절히 구해주면 되고 $on_p=0 ~ \& ~ on_c=0$ 인 상태를 보자.

자식이 하나도 없다면 불가능하므로 $\infty$를 반환한다.

$\text{Optimal}=\displaystyle \sum_{c \in Child(i)} ~ \text{Min}(dp[c][0][0],dp[c][0][1])$ 이라 할 때,

Optimal을 그대로 써주려면 최소 하나의 자식이 $dp[c][0][1] \le dpc[c][0][0]$ 이여야 한다.

이 경우엔 Optimal을 그대로 반환해주고,

그렇지 않다면 $Min_{c \in Child(i)} dp[c][0][1] - dp[c][0][0]$ 을 Optimal에 더해서 반환한다.

그리디하게 가장 비용이 적게 증가하는 자식 하나에 전단지를 붙이는 경우로 선택해준다는 의미이다.

const int inf = 3e5;  
void solve() {  
   int n, m;  
   cin >> n >> m;  
   vvi edges(n);  
   for (int i = 0, u, v; i < m; i++) {  
      cin >> u >> v, u--, v--;  
      edges[u].pb(v), edges[v].pb(u);  
   }  
   vi vis(n);  
   vector<vvi> dp(n, vvi(2, vi(2, -1)));  
   int ans = 0;  
   for (int i = 0; i < n; i++) {  
      if (vis[i]) continue;  
      function<void(int, int, int, int)> fn = [&](int cur, int p_on, int c_on, int p) -> void {  
         vis[cur] = 1;  
  
         int &ret = dp[cur][p_on][c_on];  
         if (~ret) return;  
         ret = 0;  
         for (int to: edges[cur]) {  
            if (to == p) continue;  
  
            fn(to, 0, 0, cur);  
            fn(to, 0, 1, cur);  
            fn(to, 1, 0, cur);  
            fn(to, 1, 1, cur);  
         }  
  
         if (p_on) {  
            // 부모도 켜져있고 나도 키는경우  
            if (c_on) {  
               ret++;  
               for (int to: edges[cur]) {  
                  if (to == p) continue;  
                  ret += min(dp[to][1][0], dp[to][1][1]);  
               }  
               assert(ret < inf);  
            } else {  
               // 부모는 켜져있는데 내가 안키는 경우  
               // 나는 상관없지만, 자식은 안키려면 다른것한테 받아야한다.  
               //  
               for (int to: edges[cur]) {  
                  if (to == p) continue;  
                  ret += min(dp[to][0][0], dp[to][0][1]);  
               }  
               assert(ret < inf);  
            }  
         } else {  
            // 부모가 꺼져있는데 내가 키는경우  
            if (c_on) {  
               ret++;  
               for (int to: edges[cur]) {  
                  if (to == p) continue;  
                  ret += min(dp[to][1][0], dp[to][1][1]);  
               }  
               assert(ret < inf);  
            } else {  
               // 부모가 꺼져있고 나도 꺼져있는 경우  
               // 최소한 하나의 자식이 1이여야 한다.  
               // 그럴 수 없다면 inf 반환  
  
               int optimal = 0, is_leaf = 0;  
               int can_use_one = 0;  
               for (int to: edges[cur]) {  
                  if (to == p) continue;  
                  is_leaf = 0;  
                  optimal += min(dp[to][0][0], dp[to][0][1]);  
                  if (dp[to][0][1] <= dp[to][0][0]) can_use_one = 1;  
               }  
               assert(optimal < inf);  
               if (is_leaf) ret = inf;  
               else {  
                  if (can_use_one) ret = optimal;  
                  else {  
                     int mn_diff = inf;  
  
                     for (int to: edges[cur]) {  
                        if (to == p) continue;  
                        mina(mn_diff, dp[to][0][1] - dp[to][0][0]);  
                     }  
  
                     ret = optimal + mn_diff;  
                  }  
               }  
            }  
         }  
      };  
      fn(i, 0, 0, -1);  
      fn(i, 0, 1, -1);  
      ans += min(dp[i][0][0], dp[i][0][1]);  
   }  
   cout << ans;  
}