BOJ 12746 - Traffic (Large)

BOJ 12746 - Traffic (Large)

BOJ 11960 의 간선 + 정답 찾기 버전이다.

11960의 해설

간선같은 경우 $\overline{uv}$ 경로가 있다면 $u$에 $+1$, $v$에 $+1$, $lca(u,v)$에 $-2$ 를 하면 된다.

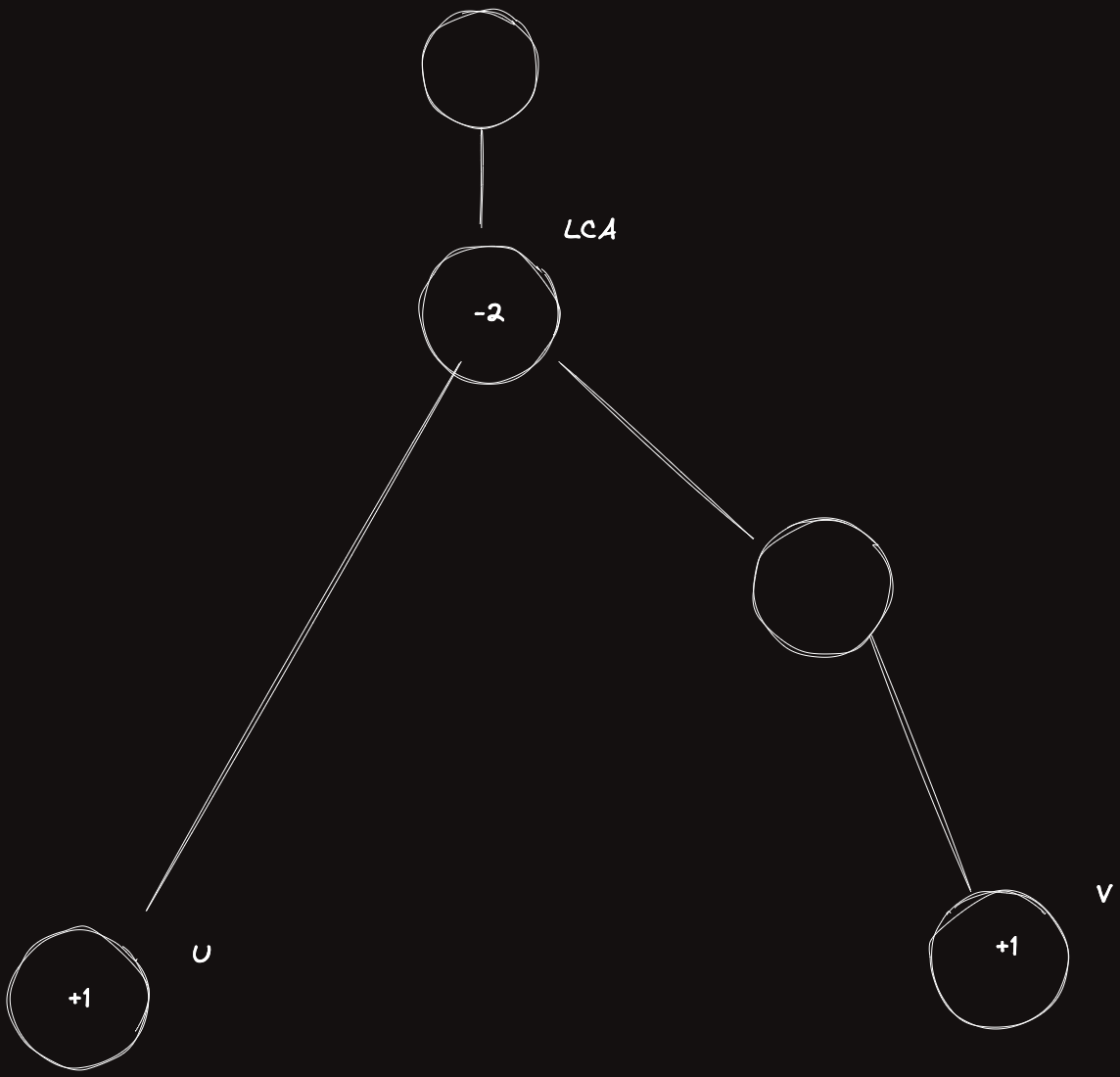
각 간선에 있는 값은 트리를 rooted tree로 구성한 후에 자신의 부모에서 자신으로 오는 간선에 대한 값이라고 하자.

$u-lca(u,v)$ 의 간선을 보면 $-2$ 의 값은 포함하지 않고 $+1$ 만 더해지기 때문에 저 간선에 한 번거치는 것이 올바르게 더해짐을 알 수 있다.

나머지도 잘 구해진다.

코드는 다음과 같다.

void solve() {  
   int n, k;  
   cin >> n >> k;  
   LCA lca(n);  
   for (int i = 0, u, v; i < n - 1; i++) cin >> u >> v, u--, v--, lca.add_edge(u, v), lca.add_edge(v, u);  
   lca.build();  
   vi psum(n);  
   while (k--) {  
      int u, v;  
      cin >> u >> v, u--, v--;  
      psum[u]++, psum[v]++;  
      int l = lca.find(u, v);  
      psum[l] -= 2;  
   }  
   vector<array<int, 3>> ans;  
   function<int(int, int)> fn = [&](int cur, int p) -> int {  
      int sum = 0;  
      for (int to: lca.edges[cur]) {  
         if (to == p) continue;  
         int tmp = fn(to, cur) + psum[to];  
         ans.pb({-tmp, min(cur, to) + 1, max(cur, to) + 1});  
         sum += tmp;  
      }  
      return sum;  
   };  
   fn(0, -1);  
   sort(all(ans));  
   cout << ans[0][1] << ' ' << ans[0][2] << ' ' << -ans[0][0];  
}