BOJ 11960 - Max Flow

HLD로 가볍게 풀 수 있지만, 정해는 트리에서의 구간합 배열이다.
트리에서 구간합 배열을 작성하는 방법은 다음과 같다.
이 문제는 정점에 대한 문제고 BOJ 12746 문제는 간선에 관한 문제이다.
정점에 대해서나 간선에 대해서나 비슷한데 구간합 배열에 처리하는 방식이 다르다.
다음은 정점에 대한 설명이다.
에서 로의 경로가 있다면 iMos 법을 트리에서 해줘야하는데, 와 에 각각 을 하고 에 를 해둔다. 또한 의 부모에도 을 한다.
이후에 어떤 정점의 서브트리의 값을 모두 더한다고 해보자.
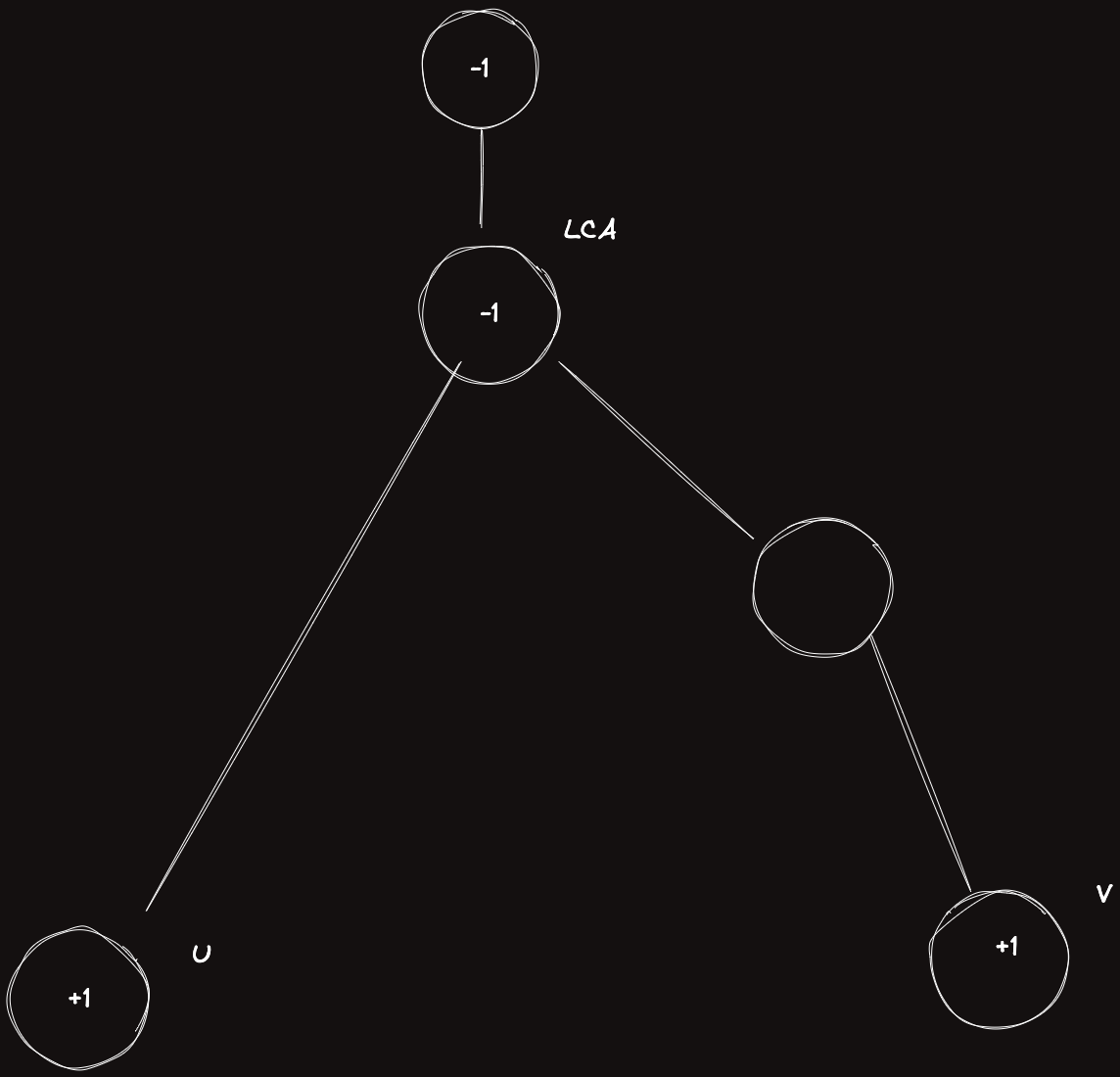
어떤 정점을 봐도 의 경로에 있는 점들은 항상 올바르게 이 되는 것을 알 수 있다.
서브트리의 합은 DFS를 하며 알 수 있다.
ETT를 써도 되지만 굳이 필요 없다.
구현은 다음과 같다.
void solve() {
int n, k;
cin >> n >> k;
LCA lca(n);
for (int i = 0, u, v; i < n - 1; i++) cin >> u >> v, u--, v--, lca.add_edge(u, v), lca.add_edge(v, u);
lca.build();
vi psum(n);
while (k--) {
int u, v;
cin >> u >> v, u--, v--;
psum[u]++, psum[v]++;
int l = lca.find(u, v);
psum[l]--;
if (~lca.p[l][0]) psum[lca.p[l][0]]--;
}
int ans = 0;
function<int(int, int)> fn = [&](int cur, int p) -> int {
int sum = psum[cur];
for (int to: lca.edges[cur]) {
if (to == p) continue;
sum += fn(to, cur);
}
maxa(ans, sum);
return sum;
};
fn(0, -1);
cout << ans;
}



Comments