2-SAT Problem
Prerequisite
2-SAT Problem
2-SAT Problem2-Satisfiability은 다음과 같다.
$n$개의 변수 $x_1, x_2, \dots, x_n$이 각각 참이나 거짓값을 가질 수 있을 때, CNFConjunctive Normal Form를 충족시킬 수 있는지와 그 해를 구하는 문제이다.
CNF란 대략 다음과 같이 생겼고, 절clause의 나열이다.
$\lor$은 OR논리 기호이고 $\land$는 AND논리 기호, 그리고 변수 앞에 붙는 $\lnot$은 부정을 의미한다.
문제 활용 예시
BOJ 2207 - 가위바위보 같은 문제를 해결할 수 있다.
문제를보면 원장선생님이 $M$번의 가위나 바위를 낸다고 한다.
원장선생님말고 학생들의 기준에서 보자. 어떤 학생이 두 가지의 추측을 하는데, 두 추측 중 하나라도 맞으면 학생이 살 수 있고, 모든 학새은 살아야 한다.
두 추측이란 것은 CNF에서 $(x_i \lor x_j)$가 충족되어야 한다는 것과 동일하다. 즉 한 명의 학생의 선택이 하나의 절을 이룬다.
모든 학생이 살아야한다는 것은 CNF에서 모든 절이 $\land$로 되어있다는 것과 동일하다. 모든 학생이 살아야 하기 때문이다.
즉, 이 문제는 결국 2-SAT문제의 해가 존재하는지 판별하는 것과 동치이다.
이건 가장 간단한 문제일 뿐이고 좀 더 복잡한 문제들은 뒤에서 살펴보자.
명제 논리
명제 논리 는 명제들간의 논리적 관계에 대해 논리적 관계를 다룬다.
당장 2-SAT의 작동 원리를 이해하기 위해서는 조건명제를 이해하면 된다.
명제 $P$전건,antecedent와 $Q$후건, consequent 그리고 $P$와 $Q$가 참 거짓이냐에 따라 조건명제 $P \to Q$가 어떤 값을 가지는지를 살펴보자.
| $P$ | $Q$ | $P \to Q$ |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
놀랍게도(?) 오로지 전건인 $P$가 참이고 후건인 $Q$가 거짓일 때만 $P \to Q$가 거짓이 나온다.
여기서 거짓이란 다시 말해 모순이다.
2-SAT문제의 해를 찾는 것은 각 변수들의 참 거짓에 대해 모순이 없는 해를 찾는 것이므로, $P \to Q$가 거짓인 경우만 만들지 않으면 된다는 것이 핵심 아이디어이다.
그래프로의 치환
놀랍게도 2-SAT문제는 그래프로 치환되어 SCC 로 해결할 수 있다.
즉, $O(N)$으로 해의 존재성과 해를 구할 수 있다.
그래프에서 각 변수(명제) $x$ 에 대해 이것 자체$(x)$와 이것에 대한 부정$(\lnot x)$를 각각 하나의 정점으로 생각해 줄 수 있다.
정점은 변수가 $n$개라면 총 $2n$개가 만들어진다.
간선들은 명제 논리에서 조건문을 의미한다. $P \to Q$ 에서 $\to$를 의미하게 된다는 것이다.
해가 없을 조건
항상 우리는 $x$와 $\lnot x$에 대해 대칭적으로 참과 거짓을 할당해야 한다.
- $x$가 참이라면 $\lnot x$는 거짓이다.
- $\lnot x$가 참이라면 $x$는 거짓이다.
2-SAT의 해가 없을(모순이 생기는) 조건은 $x$와 $\lnot x$가 싸이클을 이루는 형태이다.
$x \to \lnot x$라고 해보자. $x$에 거짓을 할당하면 $\lnot x$에 참을 할당하여 명제 논리를 결국 참으로 만들 수 있고,
$\lnot x \to x$ 여도 $\lnot x$에 거짓을 할당하면 $x$에 참을 할당하여 명제 논리를 참으로 만들 수 있다.
그러나 $x \to \lnot x \to x$ 같은 싸이클이 생겨버리는 경우엔 항상 모순이 생겨 명제 논리를 참으로 만들 수 없고 2-SAT의 해가 존재하지 않는다.
$x$와 $\lnot x$에 참과 거짓 아무거나를 각각 할당해도 명제 논리를 절대 참으로 만들 수 없기 때문이다. 이걸 참으로 만들 수 있다면 신이다.
해가 있다면 항상 대칭적으로 그래프가 생성된다.
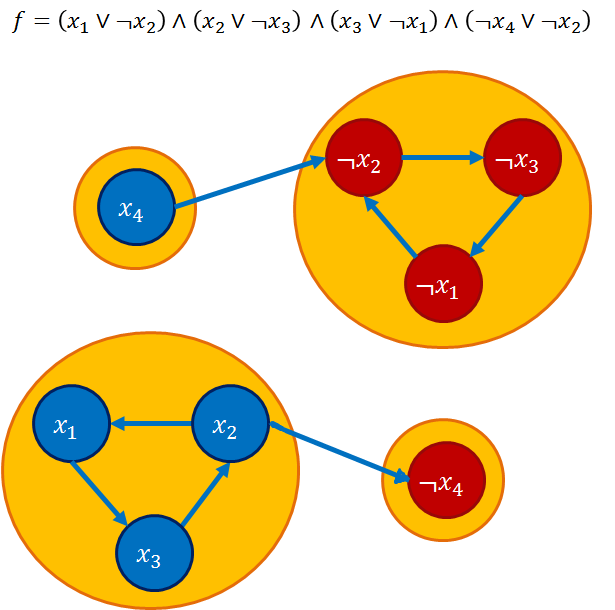
그래프에서 간선을 잇는 법
하나의 절 $(x_n \lor x_m)$를 보자. 이 절이 충족되기 위해서는 $x_n$과 $x_m$모두 거짓인 경우만 아니면 되는데,
$x_n$이나 $x_m$이 이미 참인 경우는 $(x_n \lor x_m)$이 이미 참이므로 알빠가아니고,
$x_n$이 거짓인 경우엔 $\lnot x_n$이 참이고 항상 $x_m$이 참이 되어야 절이 참이 된다.
즉, $\lnot x_n \to x_m$이 참이 되어야 한다.
반대로 $\lnot x_m \to x_n$ 이 라는 조건도 생겨서 결국 하나의 절당 두 개의 간선이 생성된다
SCC를 이용해서 해를 판별하는 법
결국 위와 같이 생성된 그래프 $G: (V, E) ~~~(n(V)=2N)$에 대해 어떤 명제 $x$에 대해 $x$와 $\lnot x$가 싸이클을 이루고 있는지를 검사하면 된다.
이 그래프는 방향 그래프이기 때문에 SCC를 써서 어떤 SCC 내부에 $x$와 $\lnot x$가 같이 있다면 해가 없다고 결론지을 수 있다.
해를 찾는법
SCC들로 재구성된 그래프는 DAGDirectional Acyclic Graph이기 때문에 재구성된 그래프에서 위상정렬을 할 수 있다.
위상정렬을 하며 현재 SCC집합의 모든 원소들에 대해 살펴본다.
이 원소를 $x$라 하자.
$\lnot x$라 해도 동일하다.
$\lnot x$가 다른 SCC그룹에서 이미 방문된 상태가 아니라면 $x$에 거짓을 할당한다.
그렇지 않다면 $x$에 참을 할당한다.
왜 거짓을 먼저 할당해야하는지는 명제 논리에서 $P \to Q$가 참이 되기위해 혹시 뒤에 $\lnot x$를 방문할 수 있기 때문에 $P$를 먼저 거짓으로 설정해버리는 것이라고 생각하면 된다.
테크닉
$x$와 $\lnot x$의 인덱스 결정
아직 2-SAT을 구현한 적이 없고 어떻게 해야할지 혼란스럽다면, 흔히 쓰이는 두 가지 방법 중, 하나를 택하도록 하자.
$0$-based index로 설명한다.
- $0 \sim n-1$ 을 원래 명제로 두고 거기에 각각 $n$씩 더한 $n \sim 2n-1$ 을 부정 명제로 둔다.
- 각 명제가 $(0, 1)$, ($2, 3)$ 이런식으로 연속된 인덱스를 갖게 하고, 홀수를 원래 명제, 짝수를 부정으로 둔다. (혹은 홀수를 부정으로 둬도 무관하다)
아래 글의 코드는 두 번째에서 홀수를 원래 명제로 두고 짝수를 부정 명제로 둔다. 의미론적으로 $0$이 부정, $1$이 원래 명제로 하는게 생각하기 편해서 그렇게 습관을 잡았다.
XOR 선언
링크 를 참고하자.
임을 알 수 있어서, 결국 절 $2$개, 즉 $4$개의 간선을 추가하는 것으로 이러한 조건을 삽입할 수 있다.
위 공식을 안쓰고도 충분히 유도해낼 수 있는데, $P$와 $Q$가 둘 중 하나만 참이여야 한다면, 위처럼 둘다 $P, Q$ 인 것과 $\lnot P,\lnot Q$ 인 것을 두 절에 $\lor$로 넣어버리고 $\land$ 연산을 때려버리면 두 절 모두를 참으로 만들기 위해 각각 하나씩만 참을 나눠가져야 한다는 것이 보여진다.
void add_or(int x, int y) {
add_edge(x ^ 1, y);
add_edge(y ^ 1, x);
}
void add_xor(int x, int y) {
add_or(x, y);
add_or(x ^ 1, y ^ 1);
}
연습 문제
BOJ 11280 - 2-SAT - 3
실제로 구현을 해보자.
struct SCC {
int n, nxt_dfsn = 0;
vvi edges, scc;
vi dfsn, fin, sccn;
stack<int> s;
SCC(int n) : n(n), edges(n), dfsn(n, -1), fin(n), sccn(n) {};
void add_edge(int u, int v) { edges[u].pb(v); }
int dfs(int i) {
int ret = dfsn[i] = nxt_dfsn++;
s.push(i);
for (int to: edges[i]) {
if (fin[to]) continue;
if (dfsn[to] != -1) ret = min(ret, dfsn[to]);
else ret = min(ret, dfs(to));
}
if (ret == dfsn[i]) {
scc.emplace_back();
while (1) {
int t = s.top();
s.pop();
scc.back().pb(t);
fin[t] = 1, sccn[t] = sz(scc) - 1;
if (t == i) break;
}
}
return ret;
}
void build() {
for (int i = 0; i < n; i++) if (dfsn[i] == -1) dfs(i);
}
bool two_sat() {
for (int i = 0; i < n; i += 2) {
if (sccn[i] == sccn[i + 1]) {
return false;
}
}
return true;
}
};
inline int inv(int i) { return i ^ 1; }
void solve() {
int n, m;
cin >> n >> m;
SCC scc(n * 2);
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
int is_not = a < 0;
a = (abs(a) - 1) * 2 + 1;
if (is_not) a = inv(a);
is_not = b < 0;
b = (abs(b) - 1) * 2 + 1;
if (is_not) b = inv(b);
scc.add_edge(inv(a), b);
scc.add_edge(inv(b), a);
}
scc.build();
if (scc.two_sat()) cout << 1;
else cout << 0;
}
$x, \lnot x$가 같은 SCC내에 있는지 판단해주자.
BOJ 2207 - 가위바위보
위에서 설명한 문제이다. 해의 존재성만 찾는 문제이다.
BOJ 11281 - 2-SAT - 4
이제 실제 2-SAT의 해를 찾아보자.
2-SAT의 해를 찾는것은 위에서 설명한것 처럼 SCC의 DAG를 위상정렬하며 $x$와 $\lnot x$중 먼저 만나는 것을 거짓으로 설정하고 나머지 것을 참으로 설정한다.
즉, $x$를 먼저 만난다면 $\lnot x$가 참이 되어 $x$명제는 부정이 참인 것이고, 반대의 경우도 비슷하다.
vi two_sat() {
for (int i = 0; i < n; i += 2) {
if (sccn[i] == sccn[i + 1]) {
return {};
}
}
vi ret(n / 2), vis(n);
for (int i = sz(scc) - 1; i >= 0; i--) {
for (int x: scc[i]) {
if (!vis[x]) {
ret[x / 2] = !(x & 1);
vis[x] = vis[x ^ 1] = 1;
}
}
}
return ret;
}
코드를 보면 먼저 같은 SCC 내에 속해있는지 검사해주고, 모순이 없다면 scc를 순회하며 먼저 만나는 것을 거짓으로 설정해주고, 나머지를 참으로 설정한다.
여기서 왜 SCC를 만들어진 것의 역순으로만 돌려줘도 상관이 없냐면, DFS의 역순이 위상정렬이기 때문이다.
BOJ 3648 - 아이돌
심사위원들이 두 개의 표를 낸다고 했으므로 이것이 하나의 절이 된다.
그리고 $1$번은 항상 진출해야 하므로 $(x_1 \lor x_1)$ 절을 포함시켜주는 것으로 해결할 수 있다.
BOJ 15675 - 괴도 강산
여기서부터 기본 문제를 벗어난 문제들이 등장한다.
사실 2-SAT 문제가 어려워지면 이게 2-SAT 문제인지 뭔지 알아내는것도 쉽지않다. 이 격자랑 2-SAT이랑 무슨 상관이 있을까?
하나의 행과 열에 대해 지나가는 것을 하나의 명제라고 하자.
$y_1 \sim y_N$과 $x_1 \sim x_M$의 명제가 있고, 각각의 명제에 대한 $\lnot$은 지나가지 않는다. 라고 모델링한다.
각 보석이 있는 칸은 한번 훔친다음에 경비원이 서있으므로 두 번 지나갈 수 없다.
그러므로 모든 보석이 있는 칸에 대해 보석이 $(i, j)$에 있다면, $y_i$와 $x_j$에 대해 XOR 연산을 해준다.
왜 XOR이냐면 모든 보석을 훔치기 위해 한 번은 무조건 지나가야 하기 때문이다.
이제 위치추적기들에 대해서 생각해보자.
결국 위치추적기를 마지막엔 하나도 가지고있지 않아야 한다는 조건은 위치추적기가 $(i, j)$에 있다고 할 때, $y_i, x_j$ 가 모두 쓰이거나 모두 안쓰이거나가 되야 된다는 뜻이다.
같은 행이나 열을 두 번 사용하는 것은 의미가 없고 가져온 다음 다시 두려면 행과 열 둘 다 훑어가야하기 때문이다.
따라서 $(y_i \land x_j) \oplus (\lnot y_i \land \lnot x_j)$ 을 추가해줘야 할것만 같지만, 좀만 생각해보면 이렇게도 표현할 수 있다.
$y_i$가 참이라고 하면 $\lnot y_i$는 거짓이 되어 $x_j$가 참이 되어야 하고, 반대의 경우도 그렇기 때문이다.
전개해보았다. 결론적으로 둘은 동치이다.
어떤 식이 나오든 2-SAT을 적용할 수 있는 CNF 으로 만들기 위해서는 논리 연산에 어느정도 지식이 있어야 한다.



Comments