Strongly Connected Component
Prerequisite
- DFS
Strongly Connected Component
강한 결합 요소(SCC)는 단뱡항 그래프에서 정의되며, 그래프를 정점 그룹들로 나누는 테크닉이다.
이 정점 그룹은 어떤 정점에서 출발해도 같은 그룹에 속한 정점에 항상 도달할 수 있어야 한다.
양방향 그래프에서 정의되면 모든 정점에서 모든 정점으로 도달할 수 있으므로 SCC를 찾는 의미가 없다.
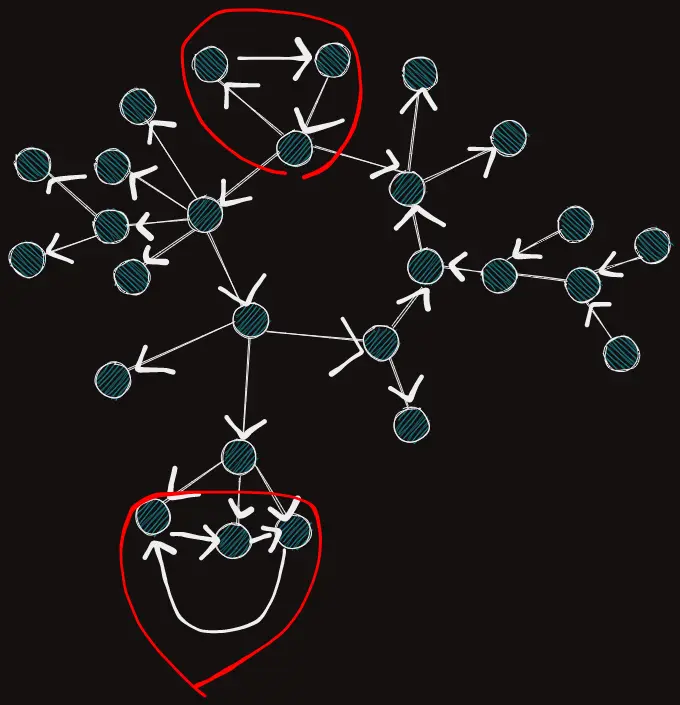
위 그림에서 빨간색으로 동그라미 친 그룹이 SCC이며, 동그라미에 속하지 않은 모든 정점 하나하나가 크기 1의 SCC라고 할 수 있다.
SCC의 활용
SCC로 저 그룹을 찾아내면 어디에 쓸까?
어떤 SCC 그룹 $A$와 $B$가 있을 때, $a \in A,~b \in B$ 이고 $a \to b$ 라는 간선이 있다면 $A\to B$로 의 간선을 이어준다고 하자.
이렇게 모두 처리하면 SCC의 그룹들의 관계는 싸이클이 없는 방향 그래프(DAG)가 나온다.
그렇지 않다고 하면 애초에 두 그룹이 합쳐져야 했으므로 모순이다.
이 방향그래프로 위상 정렬을 하거나 해서 그래프에서 여러 문제를 해결할 수 있다. 대표적으로 다음과 같다. BOJ 4196 - 도미노
또한, 2-SAT 이라는 어떤 Conjunction Normal Form(CNF)에 대하여 해가 있는지, 해가 있다면 그 해가 무엇인지까지 검출해낼 수 있으니 할용이 무궁무진하다.
타잔 알고리즘
이걸 찾는 알고리즘은 대표적으로 타잔 알고리즘과 코사라주 알고리즘이 있다.
둘다 $O(N)$의 알고리즘이며 이 글에선 타잔 알고리즘에 대해 소개한다.
타잔 알고리즘은 DFS와 스택을 이용해서 한 번의 DFS로 $O(N)$ 으로 SCC를 검출할 수 있는 알고리즘이다.
마치 단절점을 검사하는 과정과 유사하며, DFS에서 역방향 간선(Back-edge)를 이용해 싸이클을 검출해내는 과정과도 유사하다.
-
finish라는 어떤 정점이 어떤 SCC그룹에 속했는 지를 판단하는 배열을 만든다. -
DFS 스패닝 트리를 그려나가며 각각의 방문 순서를 저장하고, 방문할 때 마다 자기 자신을 스택에 push한다.
-
DFS 함수는 아직 SCC에 속하지 않은 정점들 중 자기 자신에서 도달할 수 있는 정점들 중 가장 작은 방문 순서를 가진 정점의 방문 순서를 반환한다.
-
만약 자신의 자식에 대해서 방문 순서들을 모두 봤는데, 가장 이른 방문 순서가 자기 자신이면, SCC를 하나 검출했다는 뜻이다.
-
스택에서 자기 자신이 나올 때까지 정점들을 꺼내며 SCC를 구성해준다.
왜 이것이 작동하는지 분석하려면 그래프의 순회에서 트리 간선, 순방향 간선, 역방향 간선, 교차 간선에 대해서 다루어야 한다.
- 트리 간선: DFS 스패닝 트리에 포함된 간선
- 순방향 간선: 직계 자식이 아닌 자손으로 가는 간선
- 역방향 간선: 자신의 조상으로 가는 간선(부모 포함, 이것이 있다는건 Directional Graph에서 싸이클이 있다와 동치)
- 교차 간선: 그 외의 간선
이 때 순방향 간선은 SCC의 분석에 필요하지 않다. 라이님의 글 참고
조금 생각을 해봐야 하는건 교차 간선이다.
어떤 교차 간선이 검출될 때, 그 간선을 $a \to b$라고 한다면, $b$가 이미 SCC에 속해 있으면 그 교차 간선은 버리면 된다 finish[b] = true.
그렇지 않다면 교차 간선이라 함은 이미 $b$가 방문이 되었다는 뜻이기 때문에 $b$의 방문 순서를 가져와서 현재 minimum 값을 계산해주고 있는 방문 순서에 min 연산을 해주면 된다.
교차 간선을 이용해 SCC가 구성될 수도 있기 때문이다.
하지만 이미 $b$가 SCC에 속해있는 상태라면 그럴 일이 없으므로 finish 여부를 체크해주는 것이다.
트리 간선일 경우에만 $b$가 방문이 안되었다는 뜻이기 때문에 $b$로 DFS를 진행을 계속 시켜주고 반환값을 min연산 해주면 된다.
역방향 간선일 땐 finish[b] 가 참일 수 없으므로($b$에서의 DFS가 안끝났으므로) 역시나 동일하게 방문 순서만 가져와서 min연산 해주면 된다.
따라서 코드는 다음과 같이 나타난다.
class SCC {
public:
vvi edges, scc;
vi sn, dfsn, fin;
int N, next_dfsn = 0, size = 0;
SCC(int N) : N(N) {
edges.resize(N);
sn.resize(N);
dfsn.resize(N, -1);
fin.resize(N, 0);
}
void add_edge(int from, int to) { edges[from].pb(to); }
void find() {
for (int i = 0; i < N; i++)
if (dfsn[i] == -1)
dfs(i);
}
private:
stack<int> s;
int dfs(int cur) {
dfsn[cur] = next_dfsn++;
s.push(cur);
int low = dfsn[cur];
for (int to: edges[cur]) {
if (!fin[to]) {
if (dfsn[to] == -1) low = min(low, dfs(to));
else low = min(low, dfsn[to]);
}
}
if (low == dfsn[cur]) {
vi tmp;
while (1) {
int popped = s.top();
s.pop();
fin[popped] = true;
sn[popped] = size;
tmp.pb(popped);
if (popped == cur) break;
}
size++;
scc.pb(tmp);
}
return low;
}
};
실제로 이 코드에서 to 가 역방향인지 교차인지 뭔지까지 제대로 검출할 수 있지 않다. 왜냐면 finish는 어떤 정점의 DFS가 반환될 때 true가 되는 것이 아니라 SCC에 속해있는지의 여부를 나타내기 때문이다.
하지만 위의 결론을 봤을 때, 어떤 간선 종류이든 다음과 같이 처리할 수 있다는 것이 보여진다.
for (int to: edges[cur]) {
if (!fin[to]) {
if (dfsn[to] == -1) low = min(low, dfs(to));
else low = min(low, dfsn[to]);
}
}
SCC간의 DAG구성
sn 이 각 정점이 속해있는 SCC의 인덱스이고 edges가 각 정점으로부터의 간선, scc_edges가 SCC그룹에서 다른 SCC그룹으로의 간선이라고 하자.
다음과 같이 SCC끼리의 간선을 이어주면 된다.
void find_scc_edges() {
scc_edges.resize(size);
in.resize(size);
out.resize(size);
for (int i = 0; i < N; i++)
for (int j: edges[i])
if (sn[i] != sn[j]) {
scc_edges[sn[i]].pb(sn[j]);
out[sn[i]]++;
in[sn[j]]++;
}
}
위상 정렬을 위해 in, out 배열도 함께 구성하고 있음이 보인다.
연습 문제
이 문제는 위에서 구현한 것처럼 SCC를 찾아주고 SCC간의 간선들을 모두 이어준 다음에 in[i]=0 인 SCC 그룹의 개수를 세주는 문제이다.
어떤 SCC 그룹의 in[i]=0 이라는 뜻은 그 그룹에 있는 아무 정점(도미노)이나 무너뜨려도 SCC에 있는 그룹은 당연히 모두 넘어질 것이고 위상정렬이 되면서 다른 SCC도 무너뜨려줄 것이기 때문이다.
BOJ 18133 - # 가톨릭대학교에 워터 슬라이드를?? 위와 동일한 문제이다.



Comments