Prerequisite
Articulation Point
단절점(Articulation Point)은 연결된 그래프에서 어떤 정점을 지우고 그 정점과 연결된 간선들을 모두 제거했을 때, 그래프가 2개 이상으로 나뉘는 점을 의미한다.
대개 양방향 그래프에서 다루어진다.
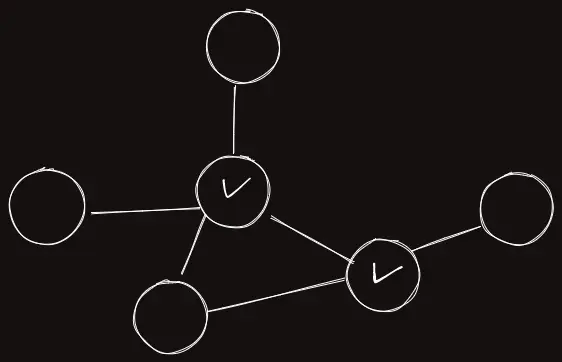
위 그림에서 체크된 노드들은 단절점이다.
이러한 단절점 알고리즘은 Strongly Connected Component나 Bi-Connected Component 같은 알고리즘 등에서 쓰인다.
알고리즘 $O(E)$
단절점은 naive 하게 구하려면 느리지만, 단 한번의 DFS만으로 구할 수 있는 방법이 있다. 따라서 시간 복잡도는 $O(E)$ 이다.
DFS나 BFS는 시간 복잡도를 $O(V+E)$ 혹은 $O(E)$ 로도 나타내곤 하나, 통상적으로 사용되는 그래프의 형태라면 큰 차이가 없어 필자는 $O(E)$를 선호한다.
DFS를 순회하며 방문한 순서대로 정점 번호를 매긴다고 하자. 대략 다음과 같아질 수 있다.
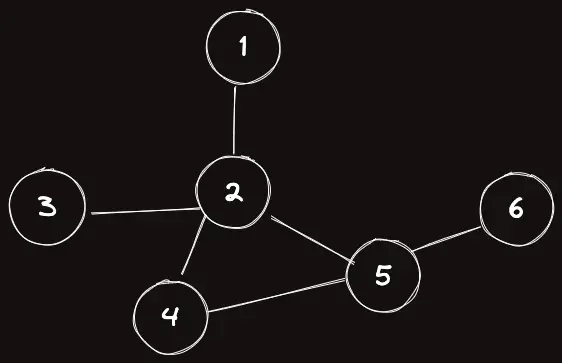
DFS 스패닝 트리에서 $2$의 자식 노드인 $3,\,4,\,5$ 같은 경우는 2를 거치지 않고 더 조상인 $1$에 도달할 수 없으므로 $2$ 는 단절점이다.
그렇다면 DFS 스패닝 트리에서 어떤 노드의 자식들이 그 노드를 거치지 않고 조상까지 갈 수 없음을 어떻게 구해주어야 할까?
DFS 재귀함수에서 반환하는 숫자를 자기 자신이 부모 노드를 거치지 않고 도달할 수 있는 가장 이른 방문 순서를 가진 노드의 번호라고 하자.
노드 $x$가 있다고 할 때,
- 노드 $x$가 루트 노트가 아니고 $x$의 자식들의 DFS 함수 반환값들 중 하나라도 $x$의 방문순서 이상이면 $x$ 는 단절점이다.
- 노드 $x$ 가 루트 노드라면 자식의 개수가 2개 이상이면 단절점이다.
단, 루트 노드와 연결된 간선의 개수만 2이상인지 세주는 것은 틀린 풀이이다. 다른 한 정점이 다른 한 정점에서의 재귀적인 경로로 통해 이미 방문되어 있을 수도 있기 때문에 DFS 스패닝 트리에서는 자식이 아닌 자손일 수 있기 때문이다.
코드로 나타내면 다음과 같다.
BOJ 11266 - 단절점 문제는 단절점을 구하는 문제이다.
int v, e;
cin >> v >> e;
vvi edges(v);
while (e--) {
int u, v;
cin >> u >> v, u--, v--, edges[u].pb(v), edges[v].pb(u);
}
int dfsn = 0;
vi order(v, -1);
vi articulation_point;
int root = -1;
function<int(int, int, int)> fn = [&](int i, int isRoot, int p) -> int {
order[i] = dfsn++;
int ret = order[i], children_cnt = 0;
for (int j: edges[i]) {
if (j == p) continue;
if (~order[j]) {
ret = min(ret, order[j]);
} else {
int earliest = fn(j, 0, i);
if (earliest >= order[i] && !isRoot) articulation_point.pb(i);
ret = min(ret, earliest);
children_cnt++;
}
}
if(isRoot && children_cnt >= 2) articulation_point.pb(i);
return ret;
};
for (int i = 0; i < v; i++) {
if (~order[i]) continue;
fn(i, 1, -1);
}
uniq(articulation_point);
cout << sz(articulation_point) << endl;
for (int i: articulation_point) cout << i + 1 << ' ';
Bridge
단절선(Bridge)는 단절점과 비슷한데, 이번엔 간선에 대해서 두 그래프를 분리하는지 찾아내는 알고리즘이다.
놀랍게도 단절점보다 구현이 매우 유사하고 쉽다. 루트노드에 따라서 분기할 필요도 없기 때문이다.
노드 $x$가 있다고 할 때,
- $x$의 자식들의 DFS 함수 반환값들 중 하나라도 $x$의 방문순서 초과면 $x$ 는 단절점이다.
단절점과 다른것은 $x$의 방문순서보다 이상이 아닌 초과로 검사해주어야 한다는 것인데, 삼각형처럼 생긴 그래프의 경우 단절선이 하나도 없는데, 방문순서 이상으로 검사를 해버리면 틀린 결과가 나온다는 걸 알 수 있을 것이다.
int v, e;
cin >> v >> e;
vvi edges(v);
while (e--) {
int u, v;
cin >> u >> v, u--, v--, edges[u].pb(v), edges[v].pb(u);
}
int dfsn = 0;
vi order(v, -1);
vector<pi> bridges;
function<int(int, int)> fn = [&](int i, int p) -> int {
order[i] = dfsn++;
int ret = order[i], children_cnt = 0;
for (int j: edges[i]) {
if(j == p) continue;
if (~order[j]) {
ret = min(ret, order[j]);
} else {
int earliest = fn(j, i);
if (earliest > order[i]) bridges.pb({min(i, j), max(i, j)});
ret = min(ret, earliest);
children_cnt++;
}
}
return ret;
};
for (int i = 0; i < v; i++) {
if (~order[i]) continue;
fn(i, -1);
}
sort(all(bridges));
cout << sz(bridges) << endl;
for (auto&[p, q]: bridges) cout << p + 1 << ' ' << q + 1 << endl;
추후엔 이 단절점과 단절선을 이용하는 알고리즘들을 정리할 것이다.




Comments