Wikipedia

요세푸스 문제Permalink

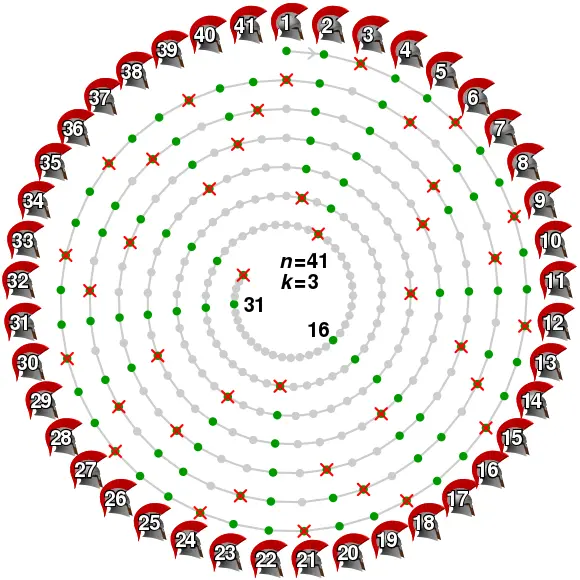
counting-out 게임의 한 종류로써, 원으로 배치된 사람들을 계속해서 처형해나가는 게임이다.

계속해서 같은 방향으로 같은 수의 사람을 건너뛰며 사람을 처형한다.

제일 마지막까지 처형당하지 않은 사람이 생존자이다.

이것의 진행을 수열로 나타내보면 다음과 같다.

$n=7$ 이고 $k=3$ 이라 해보자. $7$ 명의 사람이 있고 $3$ 명씩 건너뛰며 처형을 시킨다는 의미이다.

처음 사람의 번호를 $0$ 번이라 하자.

이렇게 최종 생존자는 $3$번($4$번 째 사람)이 된다.

문제를 푸는 법Permalink

문제는 크게 마지막에 누가 살아남냐를 구하는 것과 처형당하는 순서까지 구하는 것이 있는데, 전자는 수학적으로 생각해야하고, 후자는 노가다를 해야한다.

처형당하는 순서까지 구하는 경우Permalink

문제의 예시이다.

BOJ 1158 - 요세푸스 문제

$N, K \le 5,000$

BOJ 1168 - 요세푸스 문제 2

$N, K \le 100,000$

$N, K$가 작을 때는 아무 자료구조나 써서 직접 그 다음 $K$ 번 째가 뭔지를 찾아주어서 처형시켜주는 것으로 순열을 구할 수 있다.

$N, K$가 큰 $2$번 문제같은 경우, 세그먼트트리를 활용하여 정말 이분탐색을 쓰든 뭘 쓰든 해서 구해주면 된다.

요세푸스 순열을 구하는건 이 글의 주된 내용이 아니고 그냥 PS적인 지식으로 충분히 풀리는 구현이므로 다루지 않는다.

생존자가 누구인지만 구하는 경우Permalink

위키피디아에 있는 순서대로 필요한 것만 정리를 해보자.

$f(N, K)$ 을 최종 생존자 번호라고 하자.

$K=2$Permalink

$N$이 짝수라고 하자. 그럼 처음에는 $2,4,\dots,N$ 처럼 제거가 된다.

이제 남아있는 수들인 $1,3,\dots,N-1$ 들은 원래 처음 $1 \sim N$의 순열에서

현재 자신의 위치를 $x$ 라고 한다면, $2x-1$ 에 있던 수들이다.

$M=\dfrac N2$ 라고 한다면, $f(M)$ 은 원래 $f(2M)$ 에서 $2x-1$ 에 있던 수이므로

$N$이 홀수라고 하자.

$1$번 사람은 첫 번째 싸이클이 끝날 때 처형당한다. 그 이후에는 새로운 $2$번 째, 새로운 $4$번 째 사람이 처형당하기 시작한다.

이 경우, $x$에 있던 사람은 원래 $2x+1$ 에 있었다.

새로운 남은 사람들의 번호는 $3,5,7,\dots$ 이므로 확인해보면 맞을 것이다.

따라서, $M=\left\lfloor \dfrac N2 \right\rfloor$ 라면,

결국 $K=2$ 일 땐, $O(\log_2 N)$ 에 답을 구할 수 있다.

$K=2$ 일 때를 표로 정리해보면

와 같이 된다.

보면 $2$의 거듭제곱은 항상 $1$이고, 계속 $2$씩 증가해나가는 홀수 증가 수열을 보인다.

따라서 $n=2^m+l~~(0 \le l < 2^m)$ 이라면, $f(n)=2 \cdot l + 1$ 이여야 한다.

이렇게도 생각할 수 있다. $l$ 명이 죽은 다음에, $2^m$ 명이 남아 있다면, $2l+1$ 번 째 사람이 순열의 처음에 오도록 위치되기 때문에 생존자 $2l+1$ 이다

귀납적 증명은 사이트를 참고하자.

모든 $K$Permalink

사실 $K$가 뭐든간에 상관없이 항상 빠르게 정답을 구할 수 있다.

$K=2$는 그냥 정리해본 내용이다.

위키피디아엔 $1$부터 시작하는 인덱스로 설명이 되어있지만, $0$으로 설명하자. 그래야 더 수식과 코드가 간단하다.

사람이 $N$명 있고($0,1,\dots,N-1$) $K$ 명씩 건너뛰며 처형한다고 해보자.

처음에 $K-1$ 번째 사람이 처형당한 후에의 게임은 $K \pmod N$ 번 째 사람이 $1$번이 되어 시작되는 게임이라고 볼 수 있다.

$f(N,K)$ 를 생존자의 위치라고 할 때, 처음 한 명이 처형당한 후에는 어쨌든 $N-1$ 명이 남았으니까 $f(N-1,K)$ 라는 값이 중요하다.

그런데 첫 번째 사람이 $0$이 아닌 $K$로 바뀐 게임이므로

이 된다.

$f(1,K)=0$ 이므로, $N=1$ 일 때부터 반복하면 $O(N)$에 $f(N, K)$를 구할 수 있다.

예시

$N=7, K=3$ 이라고 하자.

여기서 $2$ 를 처형한 후의 상태는

이고, 이제 $3(=K)$ 가 첫 번째 사람이 되었다.

그런데 $N=7$ 이였으므로 $3$ 보다 왼쪽에 있는 사람들은 $7$을 더해주고 오른쪽으로 보내보자.

여기서 이제 $3(=K)$ 를 빼면 정확히 $f(6,3)=f(N-1,K)$ 인 상태, $0,1,2,3,4,5$ 가 되고, 위의 수식이 옳음을 알 수 있다.

더 빠른 접근Permalink

위의 방법은 $O(N)$ 이지만, $K$ 가 충분히 더 작다면, 놀랍게도 더 빠르게 구할 수 있다.

이 방법의 시간복잡도는 $O(K \log N)$이다.

수식을 먼저 살펴본다.

일단 $N=1$ 일땐 $f(N, K)=0$ 임은 자명하다.

$1 < N < K$ 일 때도, $K$ 가 $N$ 보다 더 작지 않으면 $O(K \log N)$ 이란 시간복잡도가 쓸모가 없으므로 앞서 구했던 수식인 $f(N,K)=f(N-1,K)+K \pmod N$ 을 이용해준다.

그렇지 않고 $K \le N$ 인 경우를 보자.

$K,2K,3K,\dots$ 번 째 사람들을 모두 죽였다고 생각해보자.

한번에 $\Bigl\lfloor \dfrac NK \Bigr\rfloor$ 명을 처형한 것과 같다.

남은 수는 $N-\left\lfloor \dfrac NK \right\rfloor$ 명이고, 이제 $f\left(N-\left\lfloor \dfrac NK \right\rfloor, K\right)$ 라는 값이 우리의 관심사이다.

Stack Overflow 답변 를 참고하면,

$N=10, K=3$ 이라고 하자. 처음에 $3$ 명이 죽는다. 이제 $N \coloneqq 7$ 이다.

0 1 2 3 4 5 6 7 8 9    n=10, k=3
1 2   3 4   5 6   0    n=7,  k=3

여기서 $N=7$ 인 쪽에 있는 사람들의 넘버링이 어떻게 $N=10$ 쪽에서 변환된건지 살펴보자.

일단 처음에 $9 \to 0$ 이 된건 $10 \% 3$ 이 더해진 것이다. 따라서 모든 수가 $N ~\%~ K$ 만큼 더해졌다고 하면 $f(N-\left\lfloor N/K \right\rfloor,K)$ 에서 $N ~\%~ K$ 를 뺐다고 하자.

보면 $N=7$ 에서 $1, 2$ 그룹은 $0$이 더해지고, $3,4$ 그룹은 $1$이 더해지고, $5, 6$ 그룹은 $2$가 더해짐이 보인다.

이건 $K-1$ 개씩 그루핑이 되있기 때문에 $\left\lfloor \dfrac h{K-1} \right\rfloor$ 를 더 더해줘야 한다.

그리고 $h<0$ 이라면 그냥 $N$ 을 더해줘서 양수로 만들어주는 것으로 정답이 된다.

위 경우에서 $N=7$ 일 때 $0$이 정답이 되어서 $N ~\%~ K$를 뺐더니 $-1$ 이 되어 $N=10$ 일 때, 정답이 $9$ 가 되는 경우를 가정해보면 된다.

실제 정답은 $N=7$ 에서 $0$은 아니다.

연습 문제Permalink

BOJ 11025 - 요세푸스 문제 3

$O(N)$ 으로 풀 수 있다.

void solve() {  
   int k, n;  
   cin >> n >> k;  
   int ans = 0;  
   for (int i = 0; i < n; i++)  
      ans = (ans + k) % (i + 1);  
   cout << ans + 1;  
}

BOJ 1179 - 마지막 요세푸스 문제

$O(K \log N)$으로 풀 수 있다.

ll k, n;  
ll f(ll n) {  
   if (n == 1) return 0;  
   if (k > n) return (f(n - 1) + k) % n;  
   ll h = f(n - n / k) - n % k;  
   if (h < 0) return h + n;  
   else return h + h / (k - 1);  
}  
  
void solve() {  
   cin >> n >> k;  
   if (k == 1) cout << n;  
   else cout << f(n) + 1;  
}