Tip - 이진 트리에서 자식의 위치 판단

이진 트리에서 $u, v~~(u<v)$ 가 있을 때, $v$가 $u$의 왼쪽 자식인지, 오른쪽 자식인지 아님 둘다 아닌지를 판단해보자.

이건 당연히 $v$ 부터 위로 타고 올라가면 $\log N$ 으로 구할 수 있지만, $O(1)$ 에 구하는 방법을 알아보자.

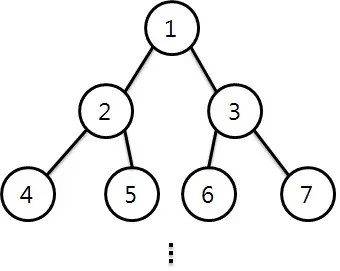
일단 $u$와 $v$의 트리에서의 레벨은 아는 상태라고 하자.

$1$번 노드의 레벨을 $0$ 으로 둔다.

레벨은 대략 다음과 같이 구할 수 있다.

int get_level(ll i) {  
   int level = 0;  
   ll cur = 1;  
   while (cur * 2 <= i) level++, cur *= 2;  
   return level;  
}

사실 이건 $\log_2 i$ 인데, 실수 오차가 없도록 구현한 것이다.

일단 $lv_u < lv_v$ 라 하자. 아니라면 자식이 될 수 없다.

높이차이 $d=lv_v-lv_u$ 를 정의한다.

$u \cdot 2^d$ 는 $lv_v$ 레벨에서 $u$ 의 자식이 될 수 있는 가장 작은 노드이다.

그런데 $lv_v$ 레벨에서 $u$ 의 자식이 될 수 있는 노드의 개수는 $2^d$ 개이므로,

결국 $u$ 의 $lv_v$ 에서의 왼쪽 자식이 되려면

범위에 있어야 하고, 오른쪽 자식이 되려면

에 있어야 한다.

즉, $u \cdot 2^d \le v < u \cdot 2^d+2^{d-1}$ 이라면 $v$는 $u$의 왼쪽 자식의 서브트리에 존재한다.

ll L = cur * pw2[d];  
ll M = left + pw2[D - 1];
ll R = (cur + 1) * pw2[d];
if (L <= i && i < M) {
  // 왼쪽 자식
} else if(M <= i && i < R) {  
  // 오른쪽 자식
}