Square Root Decomposition
제곱근 분할법이라 부르며 이름 그대로 어떤 작업을 $O(\sqrt{N})$ 에 하는 일이 잦은 알고리즘이다.
아이디어는 굉장히 단순한데, 활용법이 다양한 알고리즘 중 하나이다.
길이 $N$ 의 배열이 있다고 하자. 여기서 제곱근 분할법을 써서 구간합을 구하고 싶다.
다음과 같은 시간복잡도가 수반된다.
- 업데이트 $O(1)$
- 구간합 쿼리 $O(\sqrt{N})$
업데이트가 일어나는 상황이라면 세그먼트 트리로 $O(\log N)$ 에 구현이 가능하고 업데이트가 일어나지 않는 상황이라면 $O(1)$ 에 Sparse Table 로도 가능하지만, 이 알고리즘은 이것 말고도 다양한 쓰임새가 있다.
$M=\left\lfloor \sqrt{N} \right\rfloor$ 이라 하고, $N$ 개의 배열을 대략 $M$ 개의 그룹으로 나눈다.
그룹이라고도 하고 버킷(bucket)이라고도 흔히 부른다.
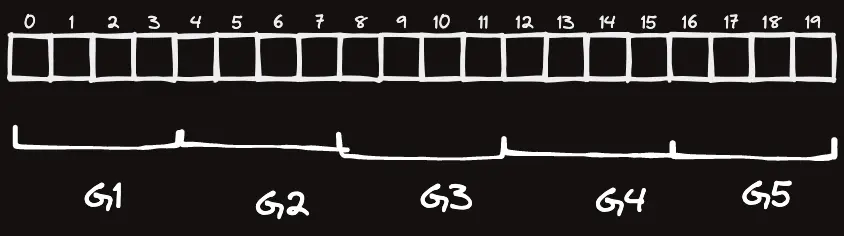
그리고 각 그룹의 원소들의 합을 구해둔다. $G_i$ 의 원소의 합을 $S_i$ 라 하자.
특정 구간 $[l, r]$ 의 구간합을 구해주고 싶다고 하자.
$[l, r]$ 에 속하는 $G_i$ 의 개수(노란 부분)는 $O(\sqrt{N})$ 이다. 왜냐면 총 $G_i$ 개수가 $O(\sqrt{N})$ 이하기 때문이다.

$l$ 이나 $r$이 속한 그룹을 $G_l,\,G_r$ 이라 할 때, $G_l,\,G_r$ 각 그룹에서 하나하나 세줘야 하는 원소의 개수(파란 부분)는 $O(\sqrt{N})$ 이다.
따라서 구간합 쿼리의 총 시간복잡도는 ${\color{salmon} O(\sqrt{N}) }$ 이다.
처음부터 $G_l=G_r$ 일 수도 있다.
인덱스 $i$의 값을 업데이트 한다고 하자. $i$ 가 속한 그룹 $G_i$ 의 원소들의 합만 업데이트 해주면 되므로 $O(1)$ 이다.
구현
대표적인 구간합 구하기 문제를 이걸로 풀어보자.
int n, m, k;
cin >> n >> m >> k;
vi a(n);
fv(a);
int sq = sqrt(n);
int B = (n + sq - 1) / sq;
vi bucket(B);
for (int i = 0; i < n; i++) {
bucket[i / sq] += a[i];
}
auto query = [&](int l, int r) {
int ret = 0;
int s = l / sq, e = r / sq;
for (int i = s + 1; i < e; i++) ret += bucket[i];
if (s != e) {
for (int i = l; i < (s + 1) * sq; i++) ret += a[i];
for (int i = r; i >= e * sq; i--) ret += a[i];
} else {
for (int i = l; i <= r; i++) ret += a[i];
}
return ret;
};
for (int i = 0; i < m + k; i++) {
int cmd, u, v;
cin >> cmd >> u >> v;
if (cmd == 1) {
u--;
bucket[u / sq] -= a[u];
a[u] = v;
bucket[u / sq] += a[u];
} else {
cout << query(u - 1, v - 1) << endl;
}
}
쿼리를 수행할 때, 우선 완전히 포함되는 bucket들의 합은 그대로 쓰고, l과 r이 같은 경우와 다를 경우를 구분해서 세준다.
구현법은 가지각색이라 정답은 없다.
연습 문제
위에서 본 문제이다.
BOJ 2912
BOJ 2912 - 백설공주와 난쟁이
$\sqrt{N}$ 개의 bucket 으로 나누자.
$[l, r]$ 에 대한 쿼리가 들어오면, 그 안엔 최대 $\sqrt{N}$ 개의 버킷이 있다.
각 버킷에 대해서 해당 버킷에서 가장 색이 많은 숫자를 골라놓는다.
이 전처리는 $O(\sqrt{N} C)$ 정도에 가능하다.
만약 $[l, r]$ 구간에 정답인 색이 존재한다면
- 구간이 모두 포함된 버킷들의 각각 가장 많은 색 $O(\sqrt{N})$ 개, 혹은
- 구간에 포함되지 않은 부분 원소들 $O(\sqrt{N})$ 개
안에 정답이 존재한다.
어떤 색이 특정 구간안에 세는것은 이분탐색을 이용해 $O(\log N)$에 가능하다.
void solve() {
int N, M, C;
cin >> N >> C;
vi a(N);
fv(a);
vvi colors(10001);
for (int i = 0; i < N; i++) colors[a[i]].pb(i);
auto cnt = [&](int c, int l, int r) { return ubi(colors[c], r) - lbi(colors[c], l); };
int sq = sqrt(N);
int B = (N + sq - 1) / sq;
vi bucket(B);
auto get_most_color = [&](int l, int r) {
int ret = 0;
vi cnt(C + 1);
for (int i = l; i <= r; i++) {
cnt[a[i]]++;
if (cnt[a[i]] > cnt[ret]) ret = a[i];
}
return ret;
};
for (int i = 0; i < B; i++) {
bucket[i] = get_most_color(i * sq, min((i + 1) * sq - 1, N - 1));
}
cin >> M;
while (M--) {
int l, r;
cin >> l >> r;
l--, r--;
int len = r - l + 1;
vi cand;
int s = l / sq, e = r / sq;
if (s ^ e) {
for (int i = s + 1; i < e; i++) cand.pb(bucket[i]);
cand.pb(get_most_color(l, (s + 1) * sq - 1));
cand.pb(get_most_color(e * sq, r));
} else {
cand.pb(get_most_color(l, r));
}
uniq(cand);
for (int c: cand) {
if (cnt(c, l, r) * 2 > len) {
cout << "yes " << c << endl;
goto out;
}
}
cout << "no\n";
out:;
}
}
쿼리 캐싱, BOJ 12857
BOJ 12857 - 홍준이는 문자열을 좋아해
위 글을 보면, $O(\sqrt{N})$ 과 연관지어 시간복잡도의 제한을 분석하고 증명하여 푸는 문제의 예시를 볼 수 있다.





Comments