Sparse Table
Sparse Table
Sparse Table(희소 배열)은 활용이 다양한 자료구조로써 정해진 구현의 형태를 띄는것이 아닌, 대략 다음과 같이 생겨서 여러가지 쿼리를 날리기 쉽게 만든 자료구조를 말한다.
T[logN][N]
이 테이블로 뭘 할 수 있는지는 살펴볼것이고, 먼저 공간 복잡도는 $O(N\log N)$ 이고 전처리에 필요한 시간복잡도도 그와 같다.
T[N][logN] 과 같은 형태를 띌 수 있고, 필자도 그렇게 사용해왔지만 캐시와 관련된 이유때문에 T[logN][N] 형식으로 구현을 하는것이 시간적으로 이득을 챙길 수 있다고 하니, 이 글에서도 그렇게 구현하도록 하겠다.
Sparse Table의 구조
T[logN][N] 과 같은 배열은 보통 T[k][i] 에 다음과 같은 정보를 담게된다.
$T_{k,\,i}$ = $i$ 에서 시작된 어떤 연산의 $2^k$ 라는 수와 연관되어 거듭된 결과
말이 모호하지만, 예시들을 보다보면 자연스레 이해하게 될 것이다.
여기서 연산은 최솟값, 최댓값이 될 수도, $f(f(f(f…(i))))$ 의 결과나 기타 등등이 될 수도 있다.
만약 연산이 최솟값 연산이 된다고 한다면 $T_{k,\,i}=$ 범위 $[i,\,i+2^k-1]$ 에서의 최솟값을 가지기 때문에 $i$ 에서 시작하는 길이 $2^k$ 부분배열 중 최솟값이기 때문에 앞서 정의한 $i$ 에서 시작된 어떤 연산의 $2^k$ 라는 수와 연관되어 거듭된 결과라는 것이 와닿게 된다.
만약 연산이 $f^{2^k}(i)$ 를 의미하는 결과가 된다고 한다면, $i$ 에서 함수 $f$ 를 $2^k$ 거듭해 연산한 결과라고 보기 때문에 역시나 정의와 맞다.
이제 실제 예시들을 보며 조금 더 친해져보자.
Sparse Table의 활용
1. Range Minimum(or Maximum) Query (RMQ)
가장 흔한 활용처이고, 이 연산에서 Sparse Table이 가지는 장점은 무려 $O(1)$ 에 RMQ를 처리할 수 있다는 것이다.
전처리 후 연산에서의 사용
$T_{i,\,k}$가 인덱스 $i$ 에서 시작하는 길이 $2^k$ 짜리 부분배열의 최솟값이라고 해보자.
우리가 $T$ 를 전처리 해두었다고 하면, 이를 $O(1)$ 에 계산하는 법은 다음과 같다.
$[L,\,R]$ 구간에서의 최솟값을 구해주고 싶다고 하자.
이 구간의 길이는 $R-L+1$ 이고 $K=\log_{2} (R-L+1)$ 인 $K$ 를 생각해보았을 때, $T_{i,\,K}$ 와 $T_{R-2^k+1,\,K}$ 의 최솟값은 $[L,\,R]$ 구간의 최솟값이 된다.
그림을 그려 살펴보자.
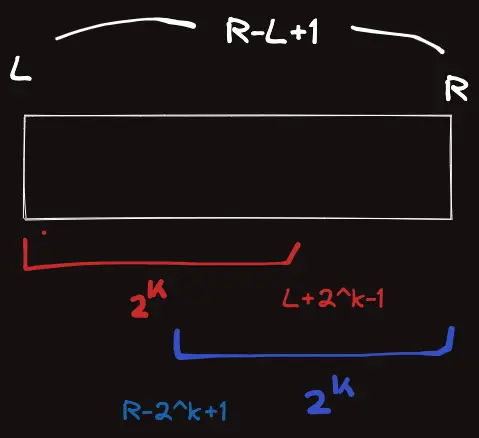
최솟값은 사칙연산과 다르게 중복되는 구간이 생겨도 결과에 영향을 미치지 않으므로 위와 같이 두 개의 구간으로 해당 구간의 길이를 커버할 수 있고, 그 구간의 길이가 바로 $2^K$ 인 것이다.
$R-L+1$ 이 $2$ 의 거듭제곱 수라서 $[L,\,L+2^k-1]$ 구간과 $[R-2^k+1,\,R]$ 구간이 일치하더라도 문제가 되지 않는다. 동일한 것 두개를 최솟값 연산을 할 뿐이다.
전처리 과정과 구현
일단 대략 $2^M > N$ 이 되는 $M$ 을 잡고 이만큼 T[logM][N] 의 배열을 할당한다.
$k=0$ 인 부분을 채워준다.
T[0][i] = A[i] 임을 알 수 있다. A 는 기존 배열이다.
이제 $k=1$ 인 부분부터 어떻게 해야될지 보자.
예를 들어, $[1,~8]$ 구간의 길이는 8인데, 여기서의 최솟값은 $[1,~4]$ 구간과 $[5,~8]$ 구간에서의 각각의 최솟값들의 최솟값이다.
이는 $T_{i,\,k}=Min(T_{i,\,k-1},~T_{i+2^{k-1},~k-1})$ 가 됨을 의미한다.
따라서 $k$ 에 대해 $k-1$ 에서의 계산된 결과들을 통해 $O(1)$ 에 값을 하나 채울 수 있다.
따라서 $dp$ 테이블을 채워주듯이 채워줄 수 있다.
코드는 다음과 같다.
int n, m;
cin >> n >> m;
int M = 18;
vvi T(M, vi(n));
for (int i = 0; i < n; i++) cin >> T[0][i];
for (int k = 1; k < M; k++)
for (int i = 0; i + (1 << k) - 1 < n; i++)
T[k][i] = min(T[k - 1][i], T[k - 1][i + (1 << (k - 1))]);
보면 중첩된 for 문에서의 i 의 범위가 조금 의아한데, 현재 $k=4$ 라서 길이 $16$ 를 의미하는 테이블의 데이터를 채우고 있는데, $i>N-16$ 이라면 $i$ 에서 시작되는 길이 16길이의 부분 배열은 구할 수 없으므로 이를 방지해준 것이다.
연습 문제
BOJ 10868 - 최솟값 문제를 보자.
값의 업데이트가 없고 그저 RMQ 를 엄청나게 해야하는 문제이므로 Sparse Table을 쓰기에 적합하다.
쿼리에 대해서는 $\log_2{(R-L+1)}$ 의 값을 빠르게 구하기 위해 $\log_2$ 에 대한 배열을 전처리해두는 것도 좋다.
2. Functional Graph & Permutation Cycle Decomposition
앞서 말했듯이 $f^{2^k}(i)$ 의 값을 Sparse Table의 값으로 채워둘 수 있는데, 이는 Permutation Cycle Decomposition에서도 Sparse Table을 이용한 풀이가 잘 먹히게 해준다.
우린 이제 Sparse Table 만드는 법을 잘 아므로 이것들은 뭘 의미하는지 문제를 통해 파악해보자.
BOJ 22863 - 원상 복구
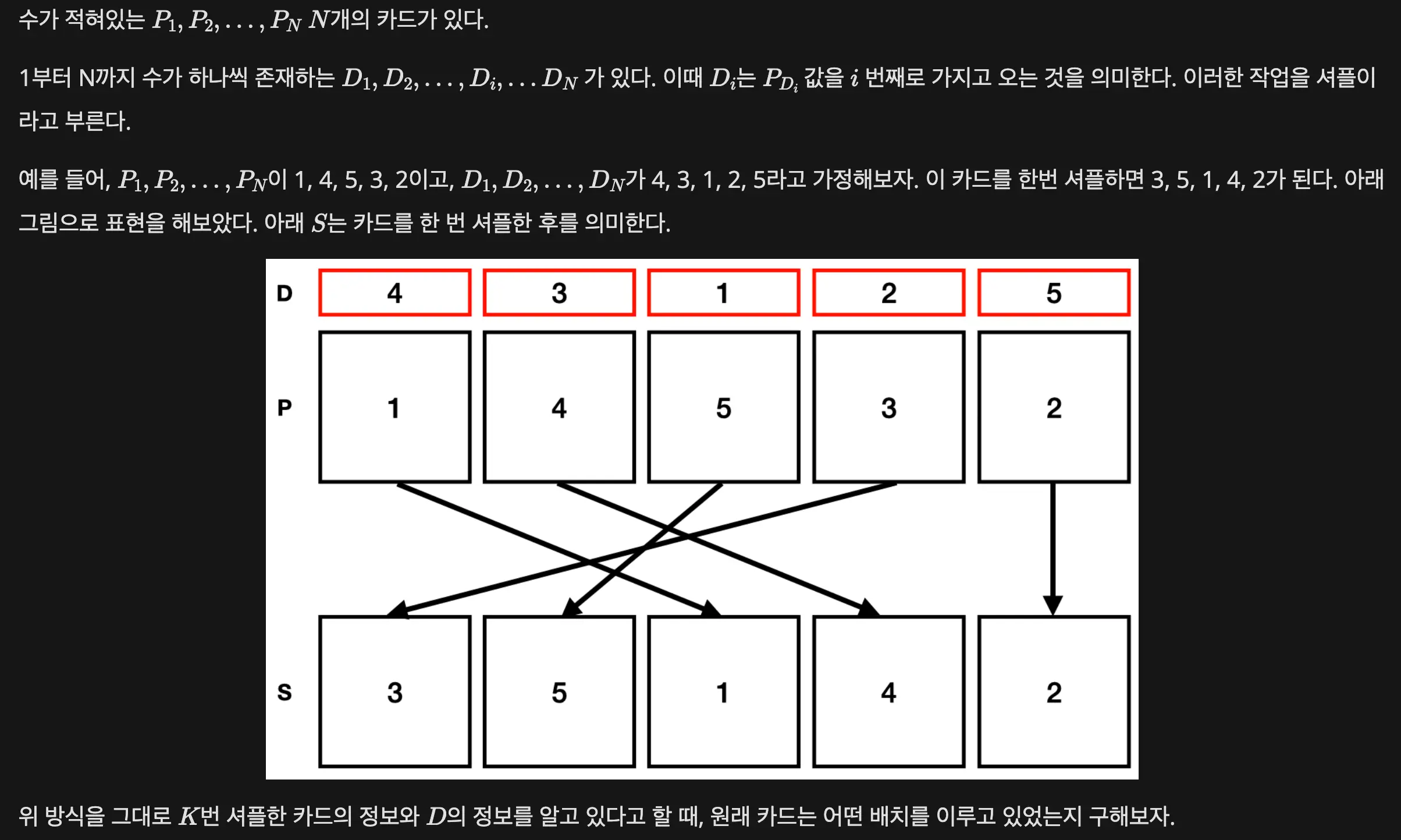
카드를 $K$ 번 셔플했고 $D$ 를 알고있다고 한다. 처음 카드의 배치를 구하라는데, $K$ 가 말도 안되게 크다.
여기서 $f=D$ 가 된다. 문제에서 말이 조금 복잡한데, $D$ 를 적용하면 카드가 한번 섞이는데 잘 보면 $i$ 에 있던 것이 $D_i$ 로 가는 것이 아니라 $D_i$ 에 있던것이 $i$ 로 오는 것이므로 이걸 반대로 해주는 연산은 $i$ 에 있던 것을 $D_i$ 로 보내는 연산이니까(역함수), $D$ 를 $f$ 로 두고 문제를 풀어주면 된다.
Permutation 은 항상 일대일 대응이므로 역함수가 항상 존재한다.
이 문제에서 일부러 $D$ 의 정의를 저렇게 해둔것은 굳이 역함수를 먼저 구한다음 그것을 $f$ 로 잡는 수고를 덜어주기 위함이다.
$T_{j,\,i}$ 가 $i$ 위치에서 시작해서 $D$ 를 $2^j$ 번 적용한 결과라고 할 때, $\displaystyle T_{j,\,i}=T_{j-1,\,T_{j-1, i}}$ 임을 알 수 있다.
int M = 60;
vvi T(M, vi(n));
for (int i = 0; i < n; i++) T[0][i] = d[i];
for (int j = 1; j < M; j++)
for (int i = 0; i < n; i++)
T[j][i] = T[j - 1][T[j - 1][i]];
이건 범위와 관련되지 않고 각 인덱스 $i$ 에 대해 계속해서 연산을 해주는 Sparse Table를 구성하는 과정이기 때문에 범위에 대한 체크가 들어갈 필요가 없다.
이제 각 인덱스 $i$ 에 대해 $D^k$ 를 적용한 결과를 하나하나씩 살펴볼텐데, 이것에 $O(\log k)$ 가 소요된다.
$k$ 를 이진수로 나타냈을 때 $1$ 이 나오는 부분들에 대해서만 $T_{j,~i}$ 를 적용시켜주는 과정이 들어간다.
vi ans(n);
for (int i = 0; i < n; i++) {
int cur = i;
for (int j = 0; j < M; j++) {
if ((1ll << j) & k) {
cur = T[j][cur];
}
}
ans[cur] = s[i] + 1;
}
전체 코드는 다음과 같다.
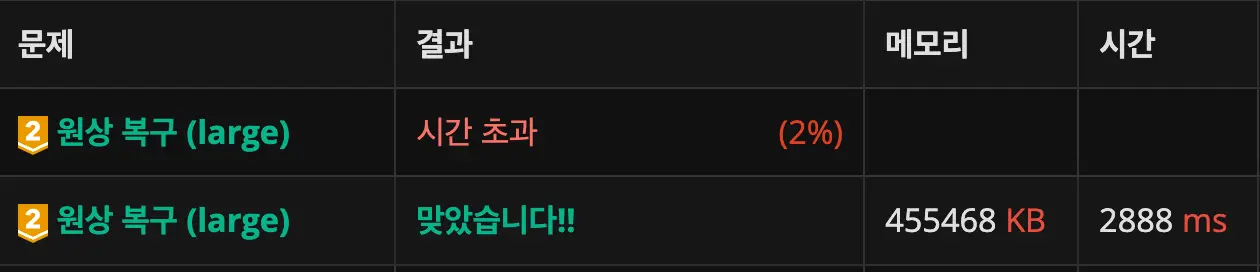
이 문제에서 시간을 검사해봤는데, 실제로 T[logN][N] 를 둘 때가 T[N][logN] 처럼 둘때보다 빠름을 알 수 있었다.
사실 이 문제는 Permutation Cycle을 분해해서 각 Cycle에 원소가 몇개가 들어가는지를 파악해 $k$ 를 나머지 연산을 통해 줄여주면 훨씬 빠르게 통과가 가능하다.
Permutation Cycle Decomposition에 대해서 곧 포스팅을 올릴 예정…
3. LCA & Parent Node
LCA(Lowest Common Ancestor) 는 트리에서 두 노드의 공통된 조상 중 가장 높이가 루트와 멀리있는 노드를 찾는 알고리즘이다.
이는 naive하게 구현하면 $O(N^2)$ 이 나오는데 (1칸씩 서로 높이가 더 높은것부터 같아질 때 까지 올라갈 것이므로), 여기서도 Sparse Table을 적용하면 빠르게 조상을 찾아버릴 수 있다.
그 아이디어는 $T_{j,\,i}$ 에 $i$ 에서의 $2^j$ 번째 부모를 저장해두는 것이다.
이는 LCA를 포스팅하며 자세히 다루도록 하겠다.
연습 문제
- 요건 해설을 블로그에 적어놨습니다.



Comments