대회 링크

간만에 백준에서 열리는 대회에 참여했고, 올솔로 5등을 했다.

대회를 밥먹고와서 풀어서 패널티는 망해있다.

난이도는 대략 다음과 같이 집계되었다.

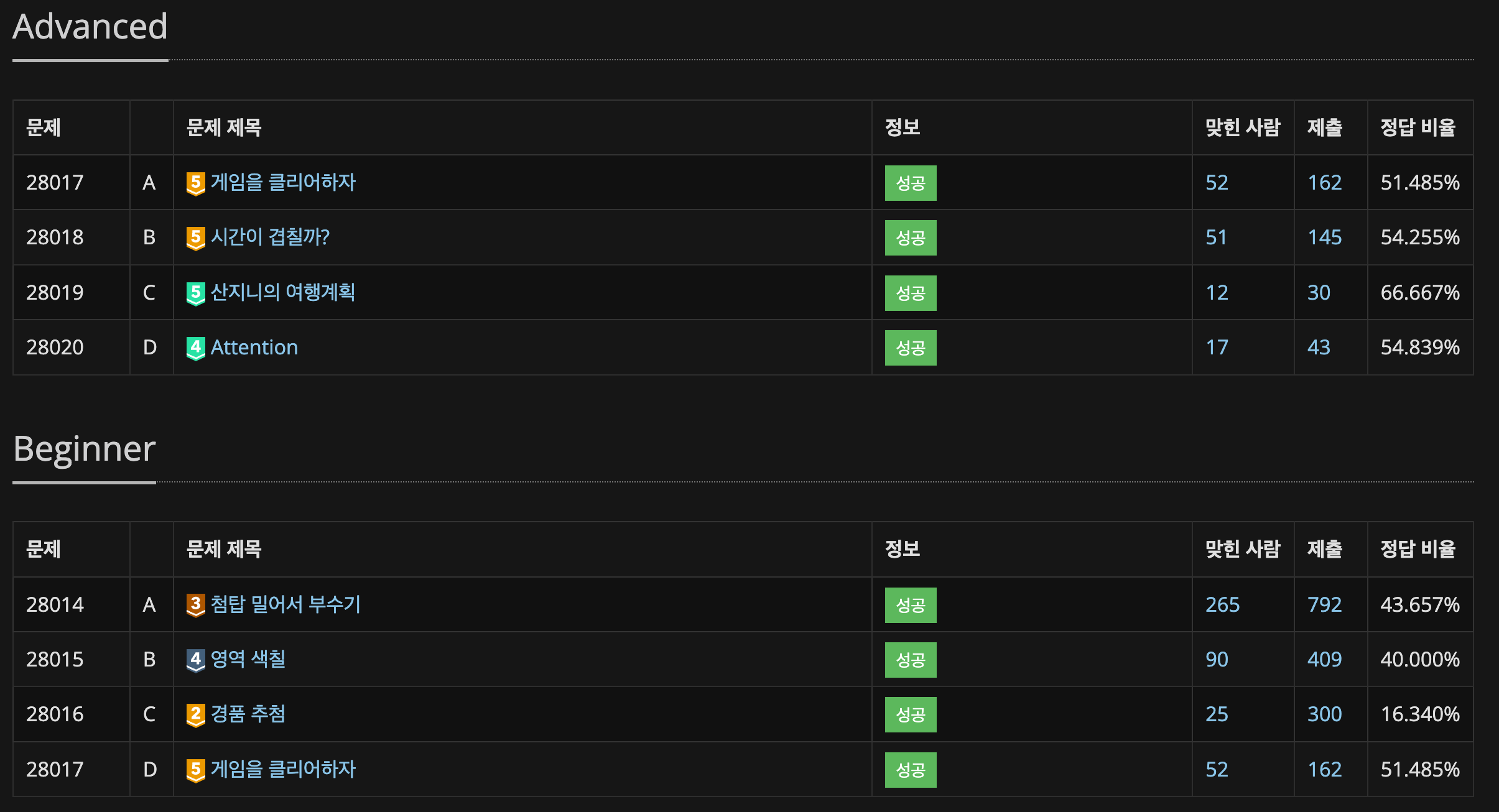
보통 난이도를 까고 풀기때문에 난이도가 없으면 체감상 좀 더 어려운데, 실제로 대회에서 체감했던 것보다 한단계씩 난이도가 낮다.

A 첨탑 밀어서 부수기Permalink

단순히 $a_{i+1} \ge a_i$ 인 것의 개수를 세면 된다.

B 영역 색칠Permalink

문제를 잘못읽어서 산을 깎는 것처럼 세는 그리디문제인줄 알았는데, 그냥 하나의 행에서 이어진 구간을 기준으로 $1$로 나뉘어진 부분과 $2$로 나뉘어진 부분을 세서 어떤 색을 처음으로 다 칠하고 나머지 색을 부분 부분 칠해줄지를 결정해주는 그리디 문제이다,

void solve() {
   int Y, X;
   cin >> Y >> X;
   vvi b(Y, vi(X));
   fv2(b);

   auto calc = [&](int y, int l, int r) -> int {
      int ret = b[y][l];
      debug(y, l, r);
      int seg1 = b[y][l] == 1, seg2 = b[y][l] == 2;
      for (int i = l + 1; i <= r; i++) {
         if (b[y][i] != b[y][i - 1]) {
            if (b[y][i] == 1) seg1++;
            else seg2++;
         }
      }
      debug(seg1, seg2);
      if (seg1 == 0 || seg2 == 0) return 1;
      return 1 + min(seg1, seg2);
   };
   int ans = 0;
   for (int y = 0; y < Y; y++) {
      int sx = -1;
      for (int x = 0; x <= X; x++) {
         if (x == X || b[y][x] == 0) {
            if (sx != -1) ans += calc(y, sx, x - 1);
            sx = -1;
         } else {
            if (sx == -1) {
               sx = x;
            }
         }
      }
   }
   cout << ans;
}

C 경품 추첨Permalink

$D, E$가 많이 풀려있어서 $C$를 스킵하려했는데 그냥 $C$부터 풀고 진행했다.

처음엔 삽질을 많이했고 당황했는데, 생각해보니 다음과 같이 풀 수 있었다.

$dp[y][x][k]$를 $(y,x)$까지 내려오는데 $k$번 두 번으로 나뉘어진 개수라고 하자.

이건 $O(N^2M)$으로 모두 구할 수 있고,

이제 $y=N-1$ 부분의 모든 $x$에 대해 이진수처럼 왼쪽으로 밀기를 반복하면 결국 어떤 곳에 가장 올 확률이 높은지 정수만 써서 계산할 수 있다.

예상대로 골드2 라는 티어가 잡혔다.

D 게임을 클리어하자Permalink

단순히 $dp[i][p]$ 를 이전에 $p$를 썼을 때 끝까지 진행하는데 최소 값이라고 할 때, $O(NM^2)$ 으로 구해줄 수 있다.

E 시간이 겹칠까?Permalink

iMos 법으로 쉽게 구할 수 있고, 구간합 배열 문제라서 세그먼트 트리가 필요없어 난이도는 높게 책정되지 않았다.

F 산지니의 여행계획Permalink

지문해석에 난항을 겪어 쓸데없이 시간을 많이썼는데, 단순히 Max MST를 구성한다음 DFS를 통해 $s$에서 이동할 때, 가장 긴 경로를 하나 빼주면 된다.

G AttentionPermalink

세그먼트 트리임은 자명해보였고, 좀더 꼬아생각해서 최고의학생 정도의 기법인줄 알았으나 그건 아니였다.

$b$에 대해 순회하며 $b[i]$가 $a$에서 있는 위치를 $j$라고 할 때, 지금까지 거쳐온 $i$들에 대해서는 $a$애서 모두 체크가 되어있는 상태이므로

현재 $i$에 대해 $b[i]$ 가$a$ 에 있는 위치 $j$ 미만의 것의 합을 세그먼트 트리로 구하면 $i$에서 문제에서 요구하는 길이 $2$인 쌍 중 $b[i]$ 로 끝나는 쌍의 개수를 구할 수 있다.

이 과정을 한 번 더 하면 길이 $3$에 대해서 구성이 가능하다.