Persistent Segment Tree
Prerequisite
- Segment Tree
- Dynamic Segment Tree
Persistent Segment Tree
이 글에서는 줄여서 PST라고 부르도록 하자.
PST는 세그먼트 트리에서 값이 업데이트 되는 과정을 메모이제이션 해둔다.
이게 어떻게 가능할까?
세그먼트 트리의 노드는 대략 $O(N)$ 개 이지만, 업데이트때는 대략 $O(\log N)$ 개만 노드가 업데이트 된다.
그렇기 때문에 $Q$ 번의 업데이트가 일어나도 새롭게 업데이트 되는(생기는) 노드 수는 $(Q \log N)$개에 국한된다.
Version
PST에서는 하나의 쿼리가 들어왔고 처리했을 때를 나타내는 트리를 Version으로 부를 수 있다.
예를 들어, 처음 세그먼트 트리는 Version=0 의 상태이다.
첫 번째 쿼리가 들어오면, Version=1 의 트리가 된다.
Version 1의 트리는 Version 0의 트리에서 첫 번째 업데이트에서 변경된 노드들만 갈아끼운 트리가 된다.
길이 4의 수열로 세그먼트 트리를 구성했다고 하자.
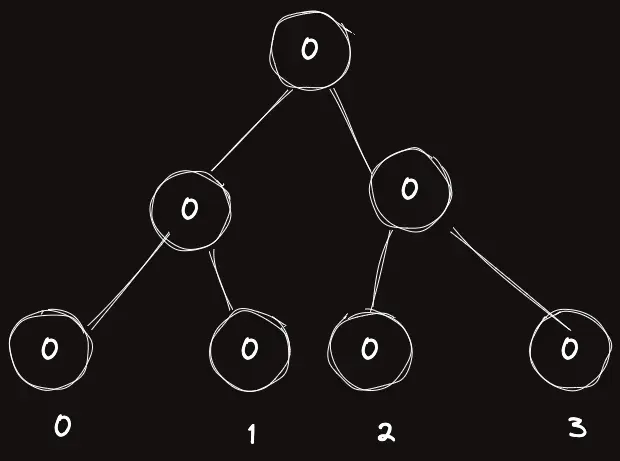
여기에 트리의 노드 번호를 매겨보자.
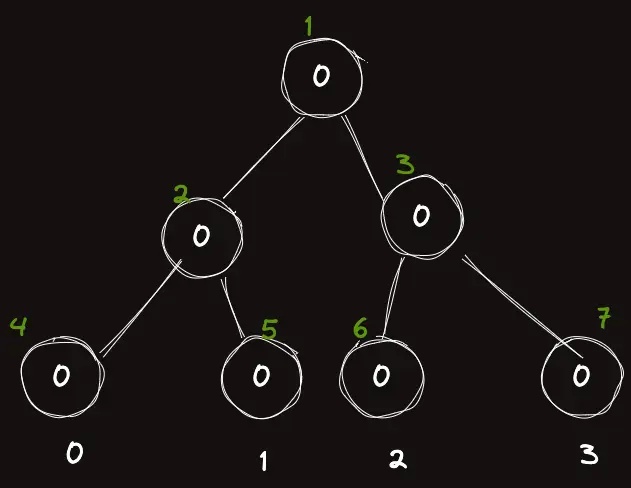
$i=2$ 에 $5$를 증가시켜보자.
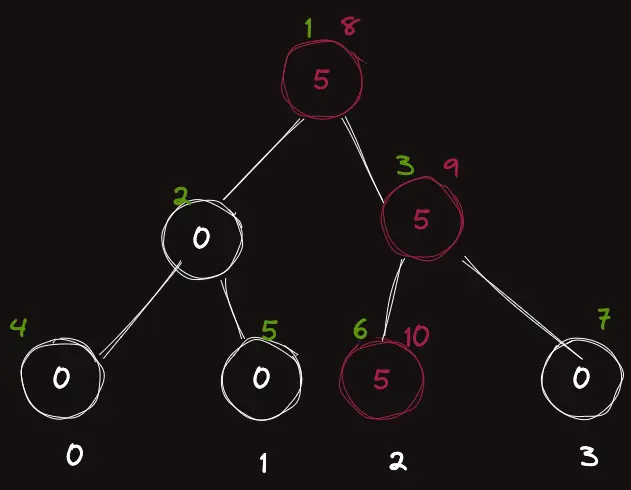
빨간색으로 교체된 노드를 표시했고, 같은 자리인데 새롭게 노드 번호가 붙은 것을 볼 수 있다.
PST는 각 Version의 루트노드의 번호를 저장하고 있는것이 중요한데, 위의 경우
| Version | index |
|---|---|
| 0 | 1 |
| 1 | 8 |
처럼 된 것이다.
업데이트 진행
위처럼 업데이트를 진행하는 방법은 다음과 같고, Dynamic Segment Tree의 그것과 유사하다.
- 업데이트 쿼리마다, 새 루트 노드를 만들고 루트 노드 테이블에 저장한다.
이제 트리를 타고 내려가는데, 현재 트리 자리에 새롭게 생긴 노드를 $cur$ 라고 하고, 현재 트리 자리에 있던 바로 직전 Version의 노드를 $prev$ 라고 하자.
- 트리를 타고 내려가며,
- 업데이트 될 노드가 왼쪽 자식이라면
- $cur$의 오른쪽 자식은 $cur_R \coloneqq prev_R$
- $cur$의 왼쪽 자식은 새롭게 만들어서 $cur_L$ 에 할당한다.
- 업데이트 될 노드가 오른쪽 자식이라면
- $cur$의 왼쪽 자식은 $cur_L \coloneqq prev_L$
- $cur$의 오른쪽 자식은 새롭게 만들어서 $cur_R$ 에 할당한다.
- 업데이트 될 노드가 왼쪽 자식이라면

이 그림에서, $8$ 의 왼쪽 노드는 $1$ 의 왼쪽 노드인 $2$와 동일하게 할당해주고, 오른쪽 노드는 새롭게 만들어 $9$ 번호를 붙여서 $8$의 오른쪽 자식으로 할당해준다.
사용성
2차원 영역 쿼리
여러가지 사용성이 있지만, 대표적으로 2차원 영역쿼리 연산이 가능하다.
$y$의 제한이 $Y$ 이고 $x$의 제한이 $X$라고 할 때, 2차원 평면 $[0, X], [0, Y]$ 에서 어떤 점에 값을 업데이트하고, 어떤 영역에 구간합을 구하라.
$XY \le 1,000,000$ 정도라면 그냥 $2$차원 Segment Tree를 써줄 수 있다.
하지만 그것보다 클 때는, PST를 이용한 풀이가 가능하다.
$2$차원 Segment Tree는 결국 $O(XY)$ 의 공간복잡도를 필요로 하기 때문이다.
다음과 같은 상황을 생각해보자.
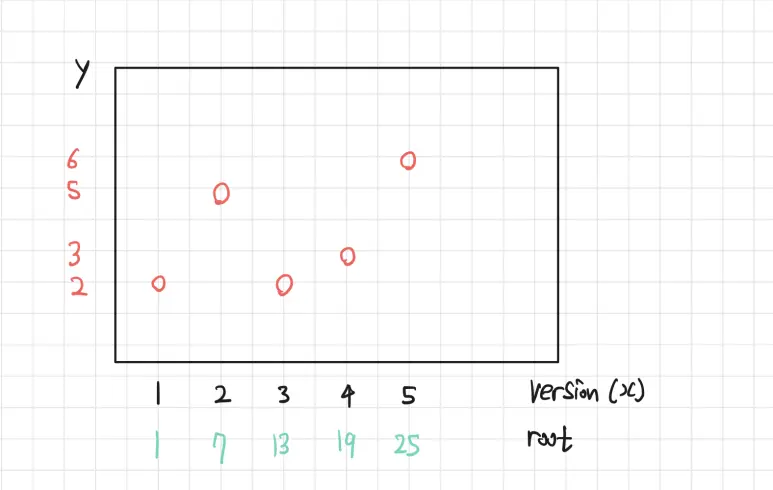
PST를 2차원에서 쓰려고 할 때, Version은 곧 $x$ 좌표를 의미하게된다.
동일한 $x$ 좌표에 여러 Version이 존재할 수도 있다. 이는 잠시 뒤 설명한다.
$Version=3$ 의 트리에서 $[2,6]$ 까지 구간합 연산을 때려버리면 다음과 같다.
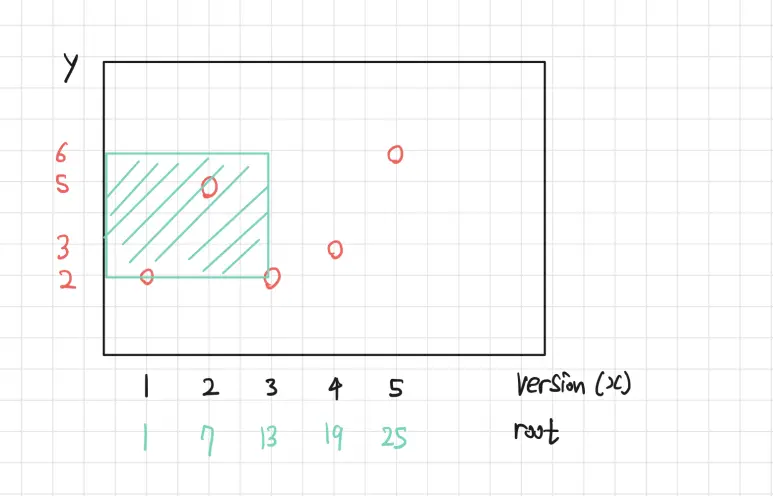
이제 여기서 $Version=1$ 의 트리의 $[2,6]$ 까지 구간합 연산을 빼버린다고 하자.
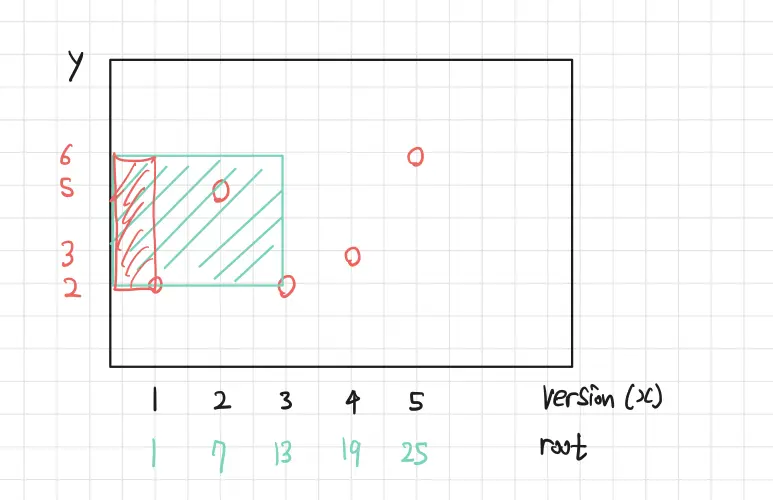
이처럼 원하는 2차원 영역에 대한 구간합 쿼리를 날릴 수 있음이 보인다.
구현은 좀 복잡하다. 각 Version이 실제로 어떤 $x$ 좌표를 나타내고 있는지도 알아야 할 것이고 무엇보다 동일한 $x$에 대해 여러 Version이 있다면, 그중 가장 늦게 만들어진 Version을 이용해서 쿼리를 날려야한다.
자세한 구현은 밑에 나온다.
1차원 구간 쿼리
왜 PST를 굳이 $1$차원에서 써야 할까?
놀랍게도 Version이 $1$ 차원에서의 인덱스 그 자체를 의미하게 만들면, 훨씬 더 무궁무진한 일들을 할 수 있기 때문이다.
예를 들어, 어떠한 $K$ 번째 값을 찾고 싶다거나, $K$보다 작은 값을 찾고 싶다거나 등등이 된다.
이에 관련한 내용은 아래 연습문제에서 살펴본다.
구현
PST는 Dynamic Segment Tree와 기본적으로 구현이 유사하기 때문에, 포인터를 이용한 구현과 배열을 이용한 구현이 있는데, 웬만하면 (정적)배열로 구현하는게 익숙해지면 더 편하고 성능상 이점을 가질 것이다.
물론 DST보다 더 복잡하고 어렵다.
구조
구조부터 살펴보자.
구현의 편의성을 위해 항상 0번 버전이 존재하고 그 때의 루트 노드가 존재한다고 할 것이다.
struct Node {
int l = -1, r = -1, v = 0;
};
struct PST {
vi version;
int N;
vector<Node> tree;
PST(int n) : N(n) {
tree.pb({});
version.pb(0);
}
};
사용할 때 버전별로 루트노드를 참고할 수 있게 vector<int> 에 version 이라고 이름지어 관리한다.
쿼리
구간합 쿼리를 작성할 것이고, 업데이트는 쿼리보다 복잡하므로 쿼리를 먼저 보자.
일반적인 Dynamic Segment Tree와 다를 이유 없다.
int query(int version_idx, int l, int r) {
return query(version[version_idx], 0, N - 1, l, r);
}
int query(int n, int nl, int nr, int l, int r) {
if (n == -1 || nr < l || nl > r) return 0;
if (nl >= l && nr <= r) return tree[n].v;
int m = nl + nr >> 1;
return query(tree[n].l, nl, m, l, r) +
query(tree[n].r, m + 1, nr, l, r);
}
업데이트
이제 업데이트를 해보자.
int update(int i, int v) {
int prev_root = version.back();
int root = sz(tree);
tree.pb({});
version.pb(root);
update(prev_root, root, 0, N - 1, i, v);
return sz(version) - 1;
}
void update(int prev, int cur, int nl, int nr, int i, int v) {
...
}
우선, PST의 업데이트 과정에서는 바로 직전 버전의 현재 노드 위치와 동일한 곳의 노드 번호를 같이 들고 다녀야하고, 이것이 prev 의 역할이다.
따라서 처음엔 바로 직전 버전의 루트를 가져와서 같이 넘겨준다.
나머지 코드는 위에서 설명한 것을 그대로 구현한 것이다.
int update(int i, int v) {
int prev_root = version.back();
int root = sz(tree);
tree.pb({});
version.pb(root);
update(prev_root, root, 0, N - 1, i, v);
return sz(version) - 1;
}
void update(int prev, int cur, int nl, int nr, int i, int v) {
if (cur == -1 || nr < i || nl > i) return;
if (nl == nr) {
tree[cur].v += v;
return;
}
// For convenience, makes previous tree always has node in this place
if (tree[prev].l == -1) {
tree[prev].l = sz(tree);
tree[prev].r = sz(tree) + 1;
tree.pb({}), tree.pb({});
}
int m = nl + (nr - nl) / 2;
if (i <= m) {
int new_child = sz(tree);
tree.pb(tree[tree[prev].l]);
tree[cur].l = new_child;
tree[cur].r = tree[prev].r;
update(tree[prev].l, tree[cur].l, nl, m, i, v);
} else {
int new_child = sz(tree);
tree.pb(tree[tree[prev].r]);
tree[cur].l = tree[prev].l;
tree[cur].r = new_child;
update(tree[prev].r, tree[cur].r, m + 1, nr, i, v);
}
tree[cur].v = (~tree[cur].l ? tree[tree[cur].l].v : 0) +
(~tree[cur].r ? tree[tree[cur].r].v : 0);
}
왼쪽에 노드를 추가할 때, 새로운 노드의 번호를 현재 tree 의 크기로 가져오고(0-based라서 이렇게 가능), 이전 버전의 트리에서의 왼쪽 자식의 값을 그대로 사용하는 것을 유의하자.
완성한 코드는 다음과 같다.
2차원 구간합에서의 사용
실제 이 트리를 사용해서 쿼리를 수행해보자.
다음과 같이 업데이트를 해준것은 무엇을 의미할까?
void solve() {
const int Y_MAX = 1e5;
PST pst(Y_MAX + 1);
pst.update(1, 1);
pst.update(2, 1);
pst.update(3, 1);
}
- $(x_0, 1)$ 지점에 $1$ 을 더한다
- $(x_1, 2)$ 지점에 $1$ 을 더한다
- $(x_2, 3)$ 지점에 $1$ 을 더한다
와 같다. 그럼 $x$ 값들은 어떻게 알 수 있는가?
그건 바로 우리가 직접 $version$ 과 매치를 시켜놓아야 한다.
그래서 update 함수에서 특별히 새롭게 생긴 version 의 인덱스를 반환하도록 했다.
void solve() {
const int Y_MAX = 1e5;
PST pst(Y_MAX + 1);
int version1 = pst.update(1, 1);
int version2 = pst.update(2, 1);
int version3 = pst.update(3, 1);
cout << pst.query(version1, 1, 3) << endl; // 1
cout << pst.query(version2, 1, 3) << endl; // 2
cout << pst.query(version3, 1, 3) << endl; // 3
}
버전 3에서는 $y=1 \sim 3$ 구간에 각각 1씩 들어있으므로 $3$이 반환되었고, 그 이전 버전들은 아직 업데이트 되기 전이므로 각각 $1, 2$가 반환된 것을 볼 수 있다.
2차원 구간에 대한 쿼리를 날리기 위해 중요한 점은 두 가지가 있다.
$x$ 가 정렬된 상태로 쿼리가 날려져야 한다.
예를 들어, $version=1$ 이 $5$ 를 의미하고 $version=2$ 이 $3$을 의미한다고 하자.
그렇다면 아까 본

와 같은 상황이 제대로 쿼리에서 수행되지 않는다.
따라서 $x$에 대해서 정렬한 쿼리를 $PST$에 넣어줌으로써(오프라인 쿼리) 적절하게 동작하도록 한다.
중복된 $x$에 대한 처리
방금전 예시는 모든 $x$가 달라서 $version$ 으로 정렬을 한다음에 쿼리를 수행하든지 하면 되지만, 같은 $x$가 있으면 조금 까다롭다.
$x_1$로 $x$가 같은 버전들 $v_1,v_2$ 가 있고 $x_2$ 인 버전 $v_3, v_4$ 가 있다고 하자 $(x_1<x_2)$
그리고 어떤 $x$구간 $[x_1+1,\,x_2]$ 에 대하여 $y$구간 $[y_1,y_2]~(y_1 \le y_2)$ 에 구간합 쿼리를 날리고 싶다고 하자.
이제 우리는 $x_2$ 인 $v$ 에서 $x_1$ 인 $v$ 를 뺌으로써 이 2차원 구간합 연산을 해야하는데, 어떤 $v$ 들을 골라야할까?
$x_2$ 인 버전들 $v_3, v_4$중에서는 가장 나중에 업데이트가 된 $v_4$ 를 루트로써 골라주어야 한다.
$v_3$ 를 고르면 $v_4$ 에서 $x_2$ 에 가해진 업데이트가 쿼리에 제대로 포함되지 않을 것이다.
$x_1$ 인 버전들 $v_1, v_2$ 에서도 가장 나중에 업데이트된 $v_2$ 를 골라주는게 맞다. $v_1$ 를 고르면 $x_1$ 에 가해진 연산인 $v_2$ 버전의 연산들이 제대로 구간합 연산에서 빼지지 않게된다.
우리가 $[x_1+1,x_2]$ 구간이 아닌 $[x_1,x_2]$ 구간에 대해서 쿼리를 날리고 싶다고 하면, $v_{0(=1-1)}$ 버전의 트리를 골라서 빼주는게 맞다.
구현에서 항상 $0$번 버전의 트리를 만들고 시작하는 것이 이럴 때 편하다.
마지막 상황을 보자.
귀찮게도 $[x_1+1,x_2-1]$ 와 같은 구간에 연산을 하고싶은데 $x_1+1$ 과 $x_2-1$ 엔 해당되는 version들이 없는 경우가 있을 수 있다.
그렇다면 더해주는 버전은 $x_2-1$ 보다 작은 $x$ 를 가진 버전 중 가장 늦게 업데이트된 버전이다.
빼주는 버전은 위에서 살펴본것과 동일하게 $x_1+1$ 보다 작은 버전 중 가장 늦게 업데이트된 버전을 사용해주면 된다.
이렇게 가장 $\sim$한 버전을 찾는 방법은 뭐 이분탐색을 구현을 해서 빠르게 찾거나 하면 된다.
어차피 트리의 시간복잡도와 상관없이 쿼리의 수에만 영향을 받으므로 $O(Q \log N)$ 정도의 시간복잡도만 총 시간복잡도에 더해지기 때문
혹은 각 $x$ 위치에 대해서 어떤 version을 참조해야 하는지 미리 전처리 해두면 $O(1)$ 에도 어떤 $x$ 에 대해서 Version을 구할 수 있다.
연습 문제
2차원 구간합
이 문제는 PST로만 풀리는 문제는 아니지만, 연습하기에 적절하다.
2차원 구간합 연산을 해주자.
const int YMAX = 1e5 + 5, inf = 1e9;
void solve() {
PST pst(YMAX);
int n, m;
cin >> n >> m;
vector<pi> query(n);
for (auto&[x, y]: query)cin >> x >> y;
sort(all(query));
vector<pi> versions;
for (auto&[x, y]: query) {
int version_idx = pst.update(y, 1);
versions.pb({x, version_idx});
}
int vidx = pst.update(YMAX - 1, 0);
versions.pb({1e9, vidx});
ll ans = 0;
while (m--) {
int x1, x2, y1, y2;
cin >> x1 >> x2 >> y1 >> y2;
if (x1 > x2) swap(x1, x2);
if (y1 > y2) swap(y1, y2);
// x2 보다 큰 버전들 중 가장 먼저 나오는 것의 바로 이전 버전
int version_right = versions[ubi(versions, mp(x2, inf))].se - 1;
int t = pst.query(version_right, y1, y2);
// x1 보다 같거나 큰 버전들 중 가장 먼저 나오는 것의 바로 이전 버전
int version_left = versions[lbi(versions, mp(x1, -inf))].se - 1;
t -= pst.query(version_left, y1, y2);
ans += t;
}
cout << ans << endl;
}
Xor 및 배열 구간에서의 K번 째 수
PST의 연습 문제로 가장 적합한 문제이다.
우선 앞서 언급했듯이, 1차원 배열에서 각 배열의 인덱스를 PST에서의 각 Version이라고 생각해줄 수 있다.
각각의 쿼리가 PST에서 어떤 연산을 의미하는지 살펴보자.
1번 연산
배열의 중앙이나 왼쪽이 아닌 제일 오른쪽 끝에 $x$ 를 추가한다는건 PST에 그대로 업데이를 해주어서 원소를 하나 추가해주며 $x$ 자리에 1을 업데이트 시켜준다는 것을 의미한다.
3번 연산
마지막 $k$ 개를 제거한다는 것은, PST가 가지고 있는 Version들 중에 제일 뒤의 $k$ 개를 제거한다는 것을 의미한다.
이 때, 실제로 pop_back 같은 짓을 하면 시간복잡도상 TLE가 나니까 다음 트리의 번호, 다음 버전의 번호와 같은 정보만 조작해주며 구현할 수 있도록 한다.
4번 연산
이건 2차원 구간합처럼 생각해볼 수 있다. $R$ 버전의 트리에서 $[0, x]$ 까지의 개수를 센다음에 $L-1$ 버전의 트리에서 $[0, x]$ 까지의 개수를 세서 빼주면 끝이다.
5번 연산
이건 tip 를 보면 이해가 쉬운데, 한 단계 더 발전시켜서 특정 노드에서 왼쪽 자식과 오른쪽 자식 두개만 보는것이 아닌, 더해줘야 할 버전의 오른쪽 자식과 왼쪽 자식, 빼줘야 할 버전의 오른쪽 자식과 왼쪽 자식 4개를 보면서 연산을 진행해야 한다.
결국,
- 왼쪽 자식 = 더해줘야 할 버전의 왼쪽 자식 개수 - 빼줘야 할 버전의 왼쪽 자식 개수
- 오른쪽 자식 = 더해줘야 할 버전의 오른쪽 자식 개수 - 빼줘야 할 버전의 오른쪽 자식 개수
처럼 되어 동일하게 구현할 수 있다.
2번 연산
2번 연산이 제일 까다롭다.
하지만 Trie 를 잘 알고 XOR과 관련된 문제들을 몇개 풀어보았다면 동일하게 구현해줄 수 있다는 것을 알 수 있다.
이 연산을 구현해주기 위해 PST를 Trie처럼 사용해야 하는데, 그러려면 PST가 가지고 있는 구간의 범위를 $2$의 거듭제곱수로 맞춰줘야한다.
예를 들어, 처음에 루트에서의 연산이 구간(nl, nr)으로 보자면$[0, 2^t-1]$ 를 의미하게 해줘야 한다는 것이다.
그렇다면 왼쪽 자식은 $[0,2^{t-1}-1]$, 오른쪽 자식은 $[2^{t-1}, 2^t-1]$ 을 의미하게 되어 정확히 왼쪽 자식들은 현재 비트가 $0$ 인 수들을 저장하게 되고, 오른쪽 자식들은 현재 비트가 $1$ 인 수들을 저장하게 된다.
$5$ 번 연산과 동일하게 더해줘야 할 버전과 빼줘야 할 버전을 두개 들고다니며 재귀적으로 찾으면 되는데, 구현에서 살펴보자.
일단 대략 1,3,4 번 쿼리만 작성이 완료된 코드는 다음과 같다.
5번 연산은 다음과 같다.
int get_kth(int n_add, int n_remove, int nl, int nr, int k) {
if (nl == nr) {
assert(k == 1);
return nl;
}
int left_add = tree[tree[n_add].l].v;
int right_add = tree[tree[n_add].r].v;
int left_remove = tree[tree[n_remove].l].v;
int right_remove = tree[tree[n_remove].r].v;
int left = left_add - left_remove;
int right = right_add - right_remove;
int m = nl + (nr - nl) / 2;
if (left >= k) {
return get_kth(tree[n_add].l, tree[n_remove].l, nl, m, k);
} else {
k -= left;
return get_kth(tree[n_add].r, tree[n_remove].r, m + 1, nr, k);
}
}
2번 연산은 다음과 같다.
int get_xor(int n_add, int n_remove, int nl, int nr, int x, int bidx) {
if (nl == nr) return nl;
int is_one = x & (1 << bidx);
int left_add = tree[tree[n_add].l].v;
int right_add = tree[tree[n_add].r].v;
int left_remove = tree[tree[n_remove].l].v;
int right_remove = tree[tree[n_remove].r].v;
int left = left_add - left_remove;
int right = right_add - right_remove;
assert(left + right);
int m = nl + (nr - nl) / 2;
if (is_one) {
if (left) {
return get_xor(tree[n_add].l, tree[n_remove].l, nl, m, x, bidx - 1);
} else {
return get_xor(tree[n_add].r, tree[n_remove].r, m + 1, nr, x, bidx - 1);
}
} else {
if (right) {
return get_xor(tree[n_add].r, tree[n_remove].r, m + 1, nr, x, bidx - 1);
} else {
return get_xor(tree[n_add].l, tree[n_remove].l, nl, m, x, bidx - 1);
}
}
}
전문은 다음과 같다.



Comments