Trie

Trie

트라이는 트리 형태의 자료구조이며, 원하는 문자열을 빠르게 검색하게 해준다.

문자열 검색에만 쓰이는 것은 아니고 트리 정점을 하나하나 타고 들어가며 무언가를 저장하거나 쿼리해야 하는 상황에서 트리의 depth가 깊지 않음 이용해 빠르게 검색을 할 수 있기 때문에 유용하다.

이에 관해서는 이따가 살펴본다.

트라이의 쓰임새는 문제에서 꽤나 티가 나는 편인데, 트라이라는 것 자체가 다음과 같은 특징을 갖고 있기 때문이다.

• 트리의 깊이가 길어지지 않는 경우에 빠르게 검색 가능
  • 예를 들어, 문제에서 문제열의 길이는 $50$을 넘지 않는다 같은 조건이 눈에 띈다면 의심해볼만하다.
• 메모리 괴물
  • 트라이는 메모리 괴물인데, 문제에서 특이하게 메모리가 $1024MB$ 나 주거나 의심이 가는 경우가 있을 수 있다.

시간 복잡도와 공간 복잡도를 어떻게 trade-off 할 수 있는지에 대해서도 구현법들을 살펴볼 것이다.

Trie의 기능들

기능은 어떤 문제에서 어떻게 사용하느냐에 따라 무궁무진하지만, 대표적으로 삽입과 검색이 있다.

삽입

그림과 함께 살펴보자.

트라이는 루트 노드가 아무것도 가리키지 않는다고 생각하면 된다.

이게 무슨 말인지는 잠시 뒤면 알게 될 것이고, foo, bar 문자열을 트라이삽입했다고 하자.

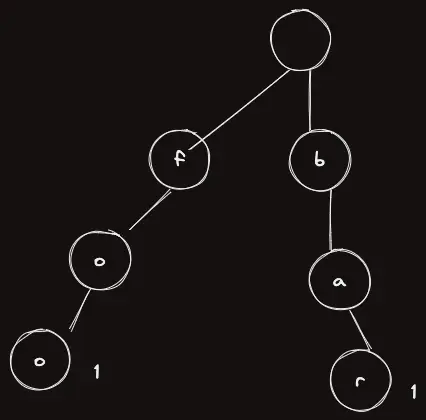
문자 한 개씩 트리에서 정점 한개를 의미하며, 쭉 이어나가게 된다.

여기서 1이라고 써진 것은 해당 정점에서 끝나는 단어가 몇개가 있는지를 의미한다.

$1$이 아닌 다른 곳은 $0$이고 이는 그림에서 생략되었다.

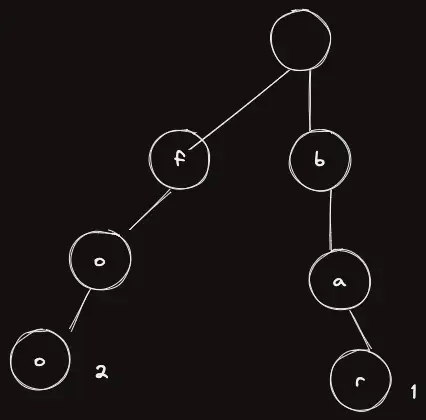
만약 우리가 foo 를 하나 더 삽입하게 되면 다음과 같을 것이다.

이제 fooxy 라는 단어를 하나 더 삽입해보자. 어떻게될까?

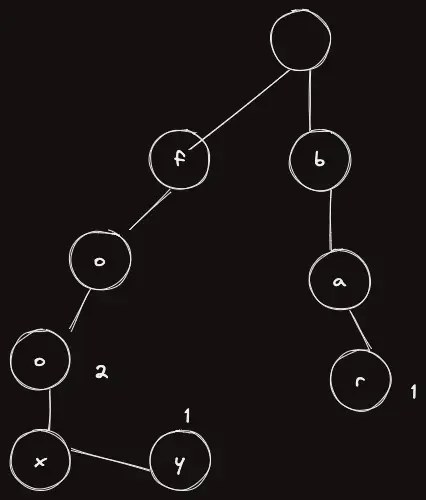
이렇게 된다.

마지막으로 baa 를 삽입한다고 하고, 결과를 예측해보자.

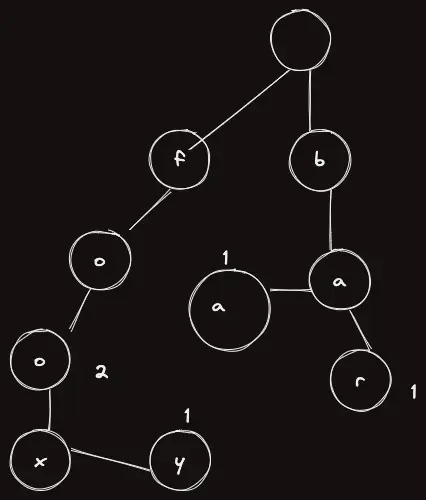
그러면 트라이에 단어들이 어떻게 삽입되는지 감을 잡았을 것이라 생각한다.

검색

위 트리에서 fo 를 검색해보자. 일단 처음에는 루트 노드에서 시작한다.

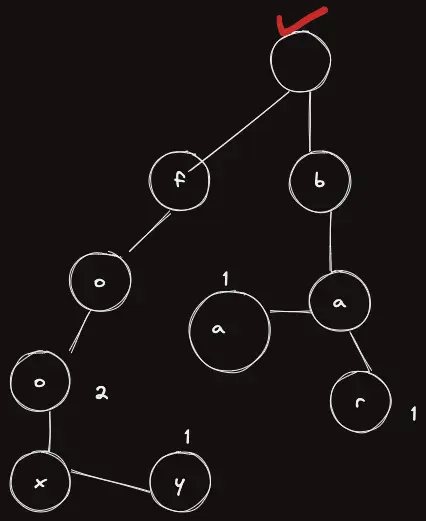
이제 첫 글자를 본다. f 이므로 f로 이동하자.

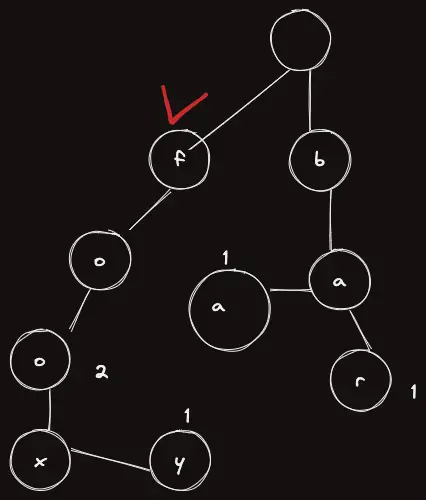
이제 다음 글자를 본다 o 이므로 o로 이동하자.

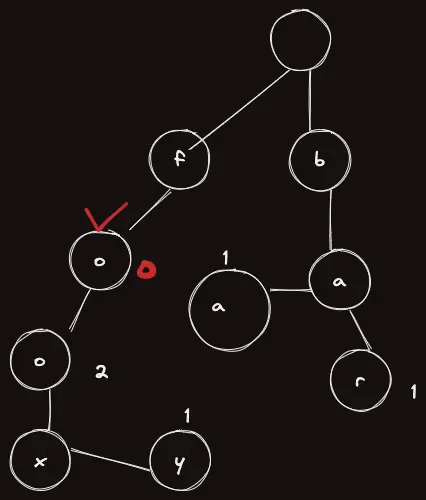
이제 더이상 처리할 문자가 없으므로, 이곳에서의 개수가 몇개인지 본다. $0$ 개 이므로 검색에 실패했다. 즉, 우리가 저장한 단어들 중에 fo는 없다.

bb 를 검색한다고 해보자. 아까와 똑같이 첫 문자를 처리하고 b 까지 간다.

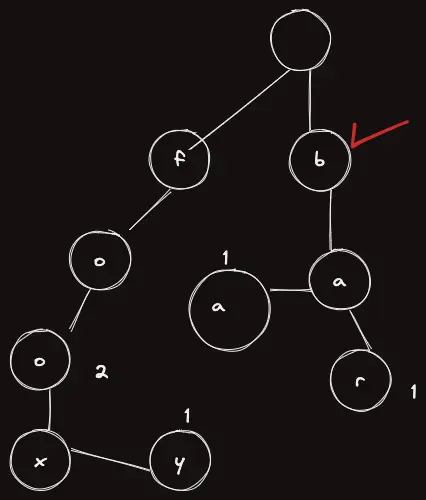
이제 두 번째 문자인 b 를 찾으려는데, 존재하는 자식 노드중에 b 를 의미하는 자식 노드가 없으므로, 이 경우에도 검색에 실패한 경우이다.

시간 복잡도와 공간 복잡도

시간 복잡도

검색

검색에 시간 복잡도는 삽입한 단어중 가장 긴 단어의 길이가 $M$ 이라면 보통 $O(M)$ 이다. 왜냐면 한 문자마다 자식 노드로 내려가며 $O(1)$ 에 처리가 된다는 가정하에 $O(M)$ 은 옳다.

자식 노드를 저장하는 방식에 따라 차이가 날 수 있지만 대개 $O(M)$ 이라고 생각하자.

삽입

삽입하려는 문자열의 길이가 $M$ 이라면 삽입도 $O(M)$ 임을 쉽게 알 수 있을 것이다.

공간 복잡도

$N$개의 문자열들의 길이가 $M_i$ 라고 할 때, $O(\displaystyle\sum_{i=0}^N M_i)$ 이다.

Trie는 문자열만 저장할 수 있을까?

Trie는 기본적으로 문자열을 저장하고 검색하는 데 쓰이는 자료구조이다.

그러나 알파벳뿐만 아니라 어떠한 문자도 키로만 나타낼 수 있으면 저장할 수 있다.

또한 문자열 뿐만 아니라 배열이라든지, 리스트같은 자료라면 저런 트리 구조를 이용해 계속해서 저장해나갈 수 있다.

Trie는 이진수와 관련된 여러 문제들을 파생시키는데, 밑에서 알아볼 것이다.

구현

간단하게 구현을 해보자.

class trie {  
private:  
   const static int range = 26;  
   const static char first_child = 'a';  
public:  
   bool output = false;  
   trie *go[range];  
   trie() { memset(go, 0, sizeof go); }  
   ~trie() {  
      for (int i = 0; i < range; i++)  
         delete go[i];  
   }  
   void insert(char *s) {  
      if (s[0] == '\0') {  
         output = true;  
         return;  
      }  
      int idx = s[0] - first_child;  
      if (!go[idx]) go[idx] = new trie();  
      go[idx]->insert(s + 1);  
   }  
   bool find(char *s) {  
      if (s[0] == '\0') return output;  
      int idx = s[0] - first_child;  
      if (!go[idx]) return false;  
      return go[idx]->find(s + 1);  
   }  
};

c++ 이지만 c 스타일의 문자열처럼 구현함으로써 편해지기 때문에 이렇게 했다. 삽입할땐 std::string 이라면 *char 로 만들어주기 위해 &s[0] 처럼 해주면 된다.

trie 는 여러 테스트 케이스가 있을 경우 메모리 초과가 나올 수 있으므로 자동으로 메모리를 초기화해주는 언어가 아니라면 c++ 같은 경우 소멸자를 이용해 메모리를 직접 초기화해주도록 하자.

• insert 는 문자열을 넣는데, 마지막 문자까지 모두 썼을 경우(널 문자를 만났을 경우), 그곳에 output를 1증가시키고 끝낸다.

만약 가려는 곳의 자식 노드가 아직 만들어지지 않았다면 먼저 만들어준다.

자식 노드를 관리하는 여러가지 방법은 아래서 자세히 살펴볼 것이다.

• find 는 insert 와 매우 비슷한데, 자신이 모든 문자열을 썼을 때 그곳에 output을 반환해주고, 계속 재귀적으로 반환해서 해당 문자열이 트라이 안에 있는지 검사해줄 수 있다.

연습 문제 - Basic

문자열은 항상 $0 \sim 9$ 만 가지고 있다고 하자.

BOJ 5052 - 전화번호 목록 이 문제를 풀 것이다.

한 번호가 다른 번호의 접두어가 되지 말아야 한다는 것은, 다음과 같이 트라이가 있을 때,

$ab$ 인 문자가 있다면 $a$ 는 있지 말아야 한다는 뜻이다.

그러면 $ab$ 를 삽입해가면서 $a$ 위치에 개수가 $1$ 이상이라면 일관성 있는 목록이 아닐 것이다.

결론적으로, 문자열의 길이가 짧은 것부터 트라이에 넣으면서 삽입하며 지나치는 경로에 다른 문자열이 이미 삽입되어 있는지(접두어인지)를 확인하면 된다.

사실 이 문제는 두 개의 함수를 만들 필요 없고, insert 함수에서만 검사하는 로직을 넣으면 끝난다.

struct trie {  
   int cnt = 0;  
   vector<trie *> children = vector<trie *>(10, 0);  
  
   ~trie() {  
      for (int i = 0; i < 10; i++) delete children[i];  
   }  
  
   bool insert(char *s) {  
      if (s[0] == '\0') {  
         cnt++;  
         return false;  
      }  
      if (cnt) return true;  
      if (!children[s[0] - '0']) children[s[0] - '0'] = new trie();  
      return children[s[0] - '0']->insert(s + 1);  
   }  
};

자식을 선언하는 방법

자식을 선언하는 방법은 문제에따라 달라져야한다. 여러가지 방법이 있지만 대표적인 것 몇개만 알아보자. 각각 장단이 있다.

1. 정적 배열과 인덱스로 관리하는 방법

위의 구현이 이걸 의미한다. 가장 무난하지만, 트리가 깊어질 경우 계속해서 배열을 가능한 자식수만큼 할당해야 하기 때문에 메모리가 부족한 문제에선 메모리 초과가 날 수 있다.

class trie {  
private:  
   const static int range = 26;  
   const static char first_child = 'a';  
public:  
   bool output = false;  
   trie *go[range];  
   trie() { memset(go, 0, sizeof go); }  
   ~trie() {  
      for (int i = 0; i < range; i++)  
         delete go[i];  
   }  
   void insert(char *s) {  
      if (s[0] == '\0') {  
         output = true;  
         return;  
      }  
      int idx = s[0] - first_child;  
      if (!go[idx]) go[idx] = new trie();  
      go[idx]->insert(s + 1);  
   }  
   bool find(char *s) {  
      if (s[0] == '\0') return output;  
      int idx = s[0] - first_child;  
      if (!go[idx]) return false;  
      return go[idx]->find(s + 1);  
   }  
};

2. 동적 배열과 탐색으로 관리하는 방법

이 방법은 특수하게 시간은 좀 널널하지만 메모리가 많이 부족할 때 써야하는 방법이다. std::map을 쓰는 방법도 결국 공간을 내부적으로 많이 차지하기 때문에 정말 메모리를 최적화하고 시간복잡도를 희생하고 싶은 경우에 사용한다.

은근히 이 구현이 아무데서나 쓰기 밸런스가 좋아서 통용해서 써도 괜찮다.

시간 복잡도는 탐색에 $O(M)$ 이 걸렸다고 하면, 가능한 자식의 가지수가 $K$라고 할 때, $O(MK)$ 가 되지만, 그것보다 현저히 빠르게 동작한다.

class trie {  
private:  
   const static char first_child = 'a';  
public:  
   bool output = false;  
   vector<trie *> go;  
   vector<int> index;  
   ~trie() {  
      for (int i = 0; i < sz(go); i++) delete go[i];  
   }  
   int find_index(int x) {  
      for (int i = 0; i < sz(go); i++) if (index[i] == x) return i;  
      return -1;  
   }  
   trie *get_child(int x) {  
      int idx = find_index(x);  
      if (idx != -1) return go[idx];  
      index.pb(x);  
      trie *new_child = new trie();  
      go.pb(new_child);  
      return new_child;  
   }  
  
   void insert(char *s) {  
      if (s[0] == '\0') {  
         output = true;  
         return;  
      }  
      int idx = s[0] - first_child;  
      get_child(idx)->insert(s + 1);  
   }  
   bool find(char *s) {  
      if (s[0] == '\0') return output;  
      int idx = s[0] - first_child;  
      if (find_index(idx) == -1) return false;  
      return get_child(idx)->find(s + 1);  
   }  
};

3. 딕셔너리로 관리하는 방법

그냥 단순히 std::map 같은 친구로 관리해주는 방법이고 1과 비슷하지만, 동적으로 메모리를 선언할 수 있다는 장점이 있다.

만약 자식 노드가 가능한 개수가 $0 \sim 9$가 아니고 막 거의 1000개 가까이 된다고 생각해보자.

그럼 1번 방법은 너무 메모리를 많이 잡아먹게 될 것이고, 2번 방법은 너무 탐색이 오래걸릴 수도 있을 것이다. 그럴 땐 바로 딕셔너리를 활용해서 구현을 해주도록 하자.

class trie {  
private:  
public:  
   bool output = false;  
   map<char, trie *> go;  
   ~trie() {  
      for (auto&[key, child]: go) delete child;  
   }  
   void insert(char *s) {  
      if (s[0] == '\0') {  
         output = true;  
         return;  
      }  
      if (!hass(go, s[0])) go[s[0]] = new trie();  
      go[s[0]]->insert(s + 1);  
   }  
   bool find(char *s) {  
      if (s[0] == '\0') return output;  
      if (!hass(go, s[0])) return false;  
      return go[s[0]]->find(s + 1);  
   }  
};

연습 문제 2

BOJ 27652 - AB 문제를 풀어보자.

일단 A와 B는 각각 트라이로 관리해주면 될 것 같다.

A의 접두사와 B의 접미사를 이어 붙여 S가 되는 경우의 수를 출력하라는 것은, A는 그냥 일반적인 Trie처럼 관리하고 B는 문자열을 뒤집은 트라이로 관리하면 된다는 것을 암시한다.

아래와 같은 상황을 보자. A와 B에 각각 $\it abcdef$ 를 넣고 $S=\it abcdef$ 쿼리가 들어온 상황이다.

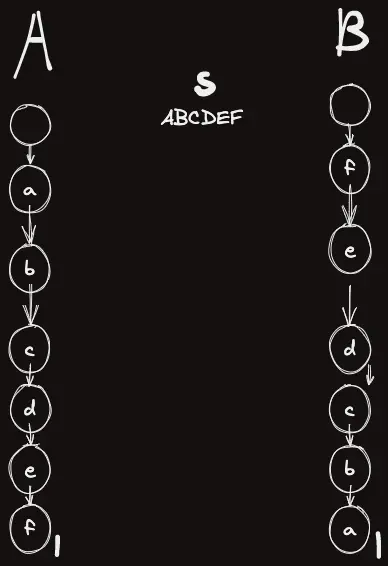
이 때의 정답은

A에서 $a$ 서브트리에서 cnt 합 + B에서 $b$ 서브트리의 cnt 합
A에서 $b$ 서브트리에서 cnt 합 + B에서 $c$ 서브트리의 cnt 합
A에서 $c$ 서브트리에서 cnt 합 + B에서 $d$ 서브트리의 cnt 합
A에서 $d$ 서브트리에서 cnt 합 + B에서 $e$ 서브트리의 cnt 합
A에서 $e$ 서브트리에서 cnt 합 + B에서 $f$ 서브트리의 cnt 합

해서 5개이다.

따라서 길이 $M$인 문자열 $S$가 들어왔을 때, 다음과 같이 A와 B의 각각 접미사, 접두사들의 길이를 구해놓고

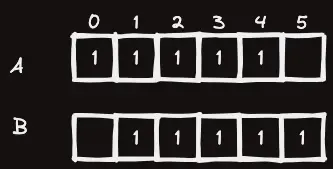
$\displaystyle\sum_{i=0}^{M-2}\left( A_i B_{i+1} \right)$ 가 정답이라는 결론이 나온다.

이제 그대로 구현해보자.

class trie {  
private:  
   const static int range = 26;  
   const static char first_child = 'a';  
public:  
   int cnt = 0;  
   trie *go[range];  
   trie() { memset(go, 0, sizeof go); }  
   ~trie() {  
      for (int i = 0; i < range; i++)  
         delete go[i];  
   }  
   void insert(char *s, int d) {  
      cnt += d;  
      if (s[0] == '\0') return;  
      int idx = s[0] - first_child;  
      if (!go[idx]) go[idx] = new trie();  
      go[idx]->insert(s + 1, d);  
   }  
   void fill_Arr(char *s, int idx, vector<int> &arr) {  
      if (s[0] == '\0' || idx >= sz(arr) - 1) return;  
      int child_idx = s[0] - first_child;  
      if (!go[child_idx]) return;  
      arr[idx] = go[child_idx]->cnt;  
      return go[child_idx]->fill_Arr(s + 1, idx + 1, arr);  
   }  
};  
  
void solve() {  
   int q;  
   cin >> q;  
   trie A, B;  
   while (q--) {  
      string cmd, type, str;  
      cin >> cmd;  
      if (cmd == "add") {  
         cin >> type >> str;  
         if (type == "A") {  
            A.insert(&str[0], 1);  
         } else {  
            reverse(all(str));  
            B.insert(&str[0], 1);  
         }  
      } else if (cmd == "delete") {  
         cin >> type >> str;  
         if (type == "A") {  
            A.insert(&str[0], -1);  
         } else {  
            reverse(all(str));  
            B.insert(&str[0], -1);  
         }  
      } else {  
         cin >> str;  
         int M = sz(str);  
         vi A_arr(M), B_arr(M);  
         A.fill_Arr(&str[0], 0, A_arr);  
         reverse(all(str));  
         B.fill_Arr(&str[0], 0, B_arr);  
  
         reverse(all(B_arr));  
  
         ll ans = 0;  
         for (int i = 0; i <= M - 2; i++)  
            ans += 1ll * A_arr[i] * B_arr[i + 1];  
         cout << ans << endl;  
      }  
   }  
}

Where to next?

원래 이 글에서 트라이를 갖고 XOR 문제들을 다루는 방법까지 알아보려고 했지만, 글의 내용을 벗어나는것 같아서 생략했다.

갑자기 난이도가 달라지기도 하고 XOR에 대한 개념을 먼저 알아야 다룰 수 있는 주제들이기 때문이다.

하지만 관심이 있다면 BOJ 13505 - 두 수 XOR 같은 문제들을 고민해 보는것도 추천한다.