Number Theory - 6.2 뫼비우스 반전공식

뫼비우스 함수

Definition 6.3

양의 정수 $n$에 대해 $\mu(n)$를 다음과 같이 정의한다.

$$ \mu(n)= \begin{cases} 1 & \text{if} ~~ n=1 \\ 0 & \text{if} ~~ p^2 \mid n, ~~p \text{는 소수} \\ (-1)^r & \text{otherwise} ~~ n=p_1p_2\cdots p_r, ~p_i \text{는 서로 다른 소수} \end{cases} $$

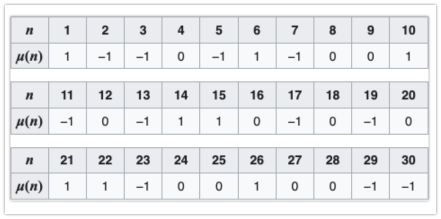
쉽게 풀어말하면, $\mu(1)=1$ 이고, 제곱인수가 있는 수는 $0$이고, 그렇지 않으면 소인수의 개수가 홀수이면 $-1$, 짝수이면 $1$ 인 함수이다.

$\mu(1)=1$ 인 것에서 눈치챘겠지만, 승법 함수이다.

$p$ 가 소수라면

• $\mu(p)=-1$
• $\mu(p^k)=0 ~~ (k \ge 2)$

이다.

이 뫼비우스 함수는 정수론 고인물 문제로 갈수록 가끔씩 튀어나와서 사람들을 괴롭히는데, 이와 관련해서 PS를 위한 정수론 챕터를 만들 때 같이 수록할 예정이다.

Theorem 6.5

함수 $\mu$는 승법 함수이다.

증명

$m$과 $n$이 서로소일 때, $m$이나 $n$중에 제곱인수가 있는 수가 있다고 해보자.

$p^2 \mid m$ 또는 $p^2 \mid n$ 이면 $p^2 \mid mn$ 이다.

따라서 $\mu(mn)=0=\mu(m)\mu(n)$. 그러면 공식은 성립한다.

이제 $m$과 $n$이 제곱인수가 없다고 하자.

$$ m=p_1p_2 \cdots p_r, ~~ n=q_1q_2 \cdots q_s $$

$$ \begin{aligned} \mu(mn)& =\mu(p_1\cdots p_rq_1 \cdots q_s)=(-1)^{r+s}\\ &=(-1)^r(-1)^s=\mu(m)\mu(n) \end{aligned} $$

따라서 $\mu$는 승법 함수다. $\square$

정수 $n$의 모든 약수의 뫼비우스 함수값 합

정수 $n$의 $\sum_{d \mid n}$ 들에 대해서 뫼비우스의 값 합인 $\sum_{d \mid n} \mu(d)$ 가 가지는 놀라운 성질을 알아보자.

$n=1$

$\sum_{d \mid 1} \mu(d)=\mu(1)=1$

$n$은 소수의 거듭제곱

$p$가 소수이고 $n=p^k$ 이라고 하자.

그럼 $n$의 약수는 $\{1,p,p^2,\dots\}$ 이다.

$\sum_{d \mid n}d=\mu(1)+\mu(p)+\mu(p^2)+\cdots=1+(-1)+0+0+\cdots$ 가 되어서 결국 $0$ 이다.

그 외

이전 단원의 Theorem으로 $F(n)=\displaystyle \sum_{d \mid n}\mu(d)$ 일 때, $F$ 도 승법함수이므로,

$n=p_1^{k_1}p_2^{k_2} \cdots p_r^{k_r}$ 이라 한다면, $F(n)=F(p_1^{k_1})F(p_2^{k_2})\cdots F(p_r^{k_r})$ 이 되고,

$F(p_i^{k_i})=0$ 임을 이전에 보였으므로 결국 $F(n)=0$ 이다.

결론적으로, $n=1$ 일 때 빼고는 모두 $\displaystyle \sum_{d \mid n}\mu(d)=0$ 이라는 결론이 나온다.

Theorem 6.6

양의 정수 $n \ge 1$에 대해,

$$ \displaystyle \sum_{d \mid n}\mu(d)=\begin{cases} 1 ~~\text{if}~~n=1 \\ 0 ~~\text{if}~~n \ne 1 \end{cases} $$

뫼비우스 반전공식

Theorem 6.7 뫼비우스 반전공식

$F$와 $f$를 다음 공식처럼 구성된 수론 함수라 하자.

$$ F(n)=\displaystyle \sum_{d \mid n}f(d) $$

그러면,

$$ f(n)=\displaystyle \sum_{d \mid n}\mu(d)F \left( \dfrac nd \right)=\sum_{d \mid n}\mu \left( \dfrac nd \right)F(d) $$

증명

정리의 결론에서, $\displaystyle \sum_{d \mid n}\mu(d)F \left( \dfrac nd \right)=\sum_{d \mid n}\mu \left( \dfrac nd \right)F(d)$ 이 성립하는 이유는, $d'$를, $d'=\dfrac nd$ 로 바꾸어도 성립하기 때문이다.

요구된 계산을 진행하자.

$$ \begin{aligned} \displaystyle \sum_{d \mid n}\mu(d)F \left( \dfrac nd \right) &=\sum_{d \mid n}\left( \mu(d) \sum_{c \mid n/d} f(c) \right)\\ =\sum_{d \mid n}\left( \sum_{c \mid n/d} \mu(d)f(c) \right) \end{aligned} $$

$F(n)=\sum_{d \mid n}f(d)$ 를 그대로 쓴 것이다.

여기서 $d \mid n$이고, $c \mid n/d$ 일 필요충분조건은 $c \mid n$이고, $d \mid n/c$ 임을 보일 수 있다.

$n = dk$라 두면, $c \mid k$ 가 되는데, $k=cx$ 라 하면, $cx \mid k, k \mid n \to c \mid n$ 이고 $\dfrac nc=dx$ 여서 $d \mid \dfrac nc$ 이다.

역방향으로도 동일하다. $d$와 $c$만 바뀐 식이란 것을 관찰할 수 있다. 이것의 예시는 밑에 정리되어있다.

이로써 식을 다시 표현하면

$$ \begin{aligned} \displaystyle \sum_{c \mid n} \sum_{d \mid n/c} \mu(d)f(c)=\sum_{c \mid n}f(c) \sum_{d \mid n/c} \mu(d) \end{aligned} $$

Theorem 6.6에 따라 $\displaystyle \sum_{d \mid n/c} \mu(d)$는 $\dfrac nc=1$ 일 때를 제외하고는 $0$이기 때문에,

$$ \begin{aligned} \displaystyle \sum_{c \mid n}f(c) \sum_{d \mid n/c}\mu(d)=\sum_{c=n} f(c) \cdot 1=f(n) \end{aligned} $$

즉, $f(n)=\displaystyle \sum_{d \mid n}\mu(d)F \Bigl(\dfrac nd \Bigr) ~~ \blacksquare$

$\sum_{d \mid n}\mu(d)$ 의 성질을 활용하는 방법이 PS에서도 시간복잡도를 줄이는데 많이 쓰인다.

예시

증명 중간에 필요충분조건을 이용해 공식을 변환하는 부분만 예시로 다시 보자.

연산을 이렇게 변환시킬 수 있다는 것을 이해하는 것도 중요하다.

$$ \begin{aligned} \displaystyle \sum_{d \mid 10} & \sum_{c \mid 10/d} \mu(d)f(c) \\\\ &=\mu(1)\left[ f(1)+f(2)+f(5)+f(10) \right]\\ &+\mu(2)\left[ f(1)+f(5) \right]\\ &+\mu(5)\left[ f(1)+f(2) \right]\\ &+\mu(10) \left[ f(1) \right]\\\\ &=f(1) \left[ \mu(1)+\mu(2)+ \mu(5)+ \mu(10) \right]\\ &+f(2) \left[ \mu(1)+\mu(5) \right]\\ &+f(5) \left[ \mu(1)+\mu(2) \right]\\ &+f(10) \left[ \mu(1) \right]\\ \\ &=\sum_{c \mid 10}\sum_{d \mid 10/c} \mu(d)f(c) \end{aligned} $$

승법 함수와 뫼비우스 반전공식

$\tau$ 함수와 $\sigma$ 함수를 생각해보자.

$$ \begin{aligned} &\tau(n)=\displaystyle \sum_{d \mid n}1 \Longleftrightarrow 1=\sum_{d \mid n}\mu(d)\tau \left( \dfrac nd \right)\\ &\sigma(n)=\sum_{d \mid n}d \Longleftrightarrow n= \sum_{d \mid n}\mu(d)\sigma \left( \dfrac nd \right) \end{aligned} $$

Theorem 6.8

$F$가 승법함수이고, $F(n)=\displaystyle \sum_{d \mid n}f(d)$ 이면, $f$또한 승법함수이다.

증명

$m$과 $n$을 서로소인 양의 정수라 하자.

$mn$의 모든 약수 $d$는 $d_1 \mid m, ~ d_2 \mid n$ 그리고, $gcd(d_1,d_2)=1$ 인 $d=d_1d_2$ 로 유일히 나타낼 수 있다.

뫼비우스 반전공식을 적용하면,

$$ \begin{aligned} f(mn)&=\displaystyle \sum_{d \mid mn} \mu(d)F \left( \dfrac {mn}d \right)\\ &=\sum_{d_1 \mid m}\sum_{d_2 \mid n}\mu(d_1d_2)F \left( \dfrac {mn}{d_1d_2} \right)\\ &=\sum_{d_1 \mid m} \mu(d_1) F \left( \dfrac m{d_1} \right) \sum_{d_2 \mid n} \mu(d_2) F \left( \dfrac n{d_2} \right)\\ &=f(m)f(n) \end{aligned} $$

따라서 $f$도 승법적이다. $\square$