Merge Sort Tree
Prerequisite
- Merge Sort
- Segment Tree
Merge Sort Tree
Merge Sort Tree는 골 때리는 자료구조인데, Merge Sort과정을 기록해두었다가 쿼리를 날릴 수 있게 해주는 녀석이다.
대개 다음과 같은 쿼리에 쓰인다.
$[L, R]$ 구간에서 $K$보다 큰 수의 개수를 찾아라.
이런 쿼리가 하나가 들어오면 $O(N)$ 에 구할 수 있겠지만, $100,000$개 씩 들어온다고 생각해보면 쉽지않다.
BOJ 13537 - 수열과 쿼리 1 바로 이런 문제이다.
수쿼 $1$이라니.. 나름 근본 자료구조일지도?
기능
- 이미 Merge Sort Tree를 구성하고는 값을 변경할 수 없다.
- Tree를 초기화하는데 $O(N \log N)$ 이 소요된다.
- 어떤 구간 $[L, R]$ 에 대해서 $K$ 이상의 수를 쿼리하는데 $O(\log^2 N)$ 이 소요된다.
원리
Merge Sort 과정을 기록해둔다는 것이 생소할 수 있는데, 사실 구현이나 원리는 세그먼트 트리와 유사하다.
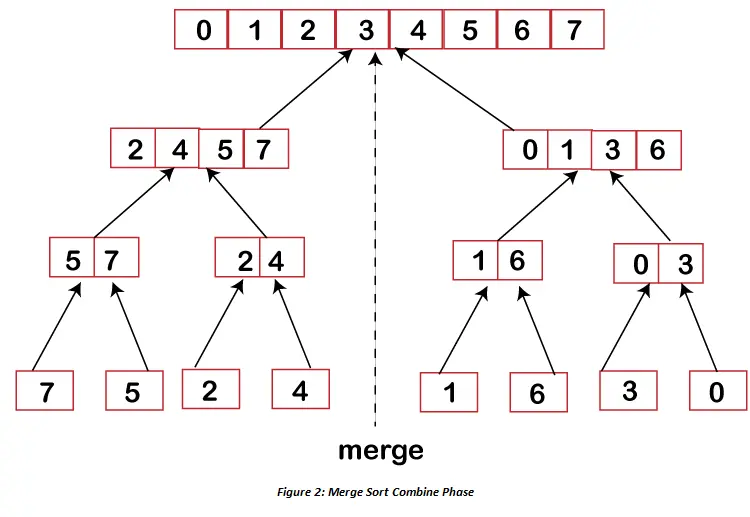
이 Merge Sort 과정을 보면, 하나의 높이에 원소가 $N$개 있고 높이가 총 $\log N$ 개 이므로 모든 네모 박스를 저장해둔다면 공간이 겨우 ${\color{salmon} N \log N}$ 밖에 필요하지 않음을 알 수 있다.
우리가 $[3, 5]~~(4,1,6)$ 구간에서 $5$ 이상의 수가 몇개인지 알고싶다고 하자.
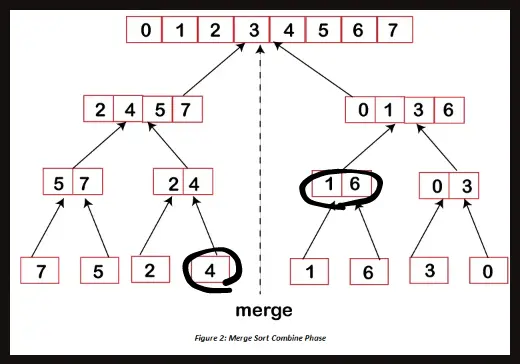
그럼 세그먼트 트리처럼 탐색을 했을 때, 위에 동그라미 친 두 노드까지 도달을 할 것이다.
그럼 각 노드는 Merge Sort 과정에서 해당 노드에서 담고있는 $(4)$ 배열과 $(1, 6)$ 배열을 각각 갖고 있을 것이다.
그럼 그 배열들에 대해서 $5$ 이상의 수가 몇개인지 아는 것은 $\log N$ 에 가능하다.
왜 $\log N$일까? 각각의 노드들은 정렬된 상태로 갖고있기 때문에 이분 탐색을 써서 그 개수를 빠르게 찾을 수 있기 때문이다.
결국 쿼리 하나에 $O(\log^2 N)$ 이 걸리게 된다.
세그먼트 트리처럼 구간을 타고 들어가는데 $O(\log N)$이 걸리기 때문이다.
구현
1. 초기화
일단 세그먼트 트리처럼 $2^{\lceil \log_2 N \rceil + 1}$ 개 정도만큼 2차원 동적 배열을 선언한다.
struct merge_sort_tree {
int size;
vector<vector<int>> tree;
merge_sort_tree(int n) {
size = 1 << int(ceil(log2(n))+1);
tree.resize(size);
}
void add(int i, T v) {
tree[i + size / 2].pb(v);
}
void init() {
// ...
}
};
이제 원래 배열에 있던 수들을 채워넣고 init 에서 Merge Sort를 시작할 것인데,
위처럼 초기화를 하면 $2^{\lceil \log_2 N \rceil + 1}$ 크기의 트리가 생기고 다음과 같이 구성이 될 것이다.
$N=5$, 배열이 $(1,2,4,8,3)$ 이라고 해보자
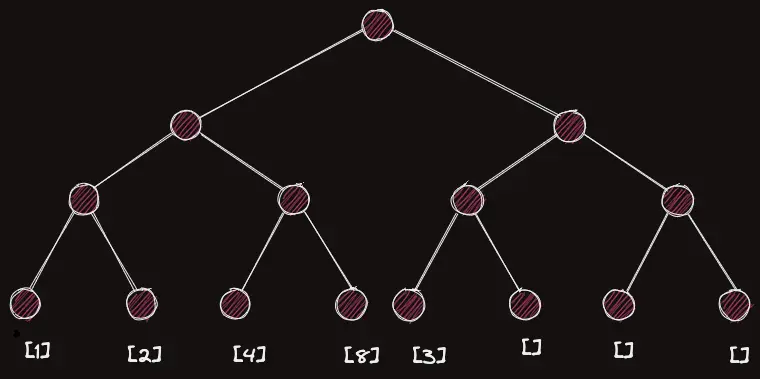
실제 노드의 개수는 15개로 보이지만, 보통 세그먼트 트리에서 왼쪽 자식은 $2i$, 오른쪽 자식은 $2i+1$ 이란 편이성을 두기 위해 루트 노드의 인덱스를 $1$로 잡으므로 실제로 $16$ 길이 배열이 선언이 된 상태이다.
이 때, $S=2^{\left\lceil \log_2 N \right\rceil + 1}$ 라고 한다면, $\dfrac S2$ 는 정수이고 $\dfrac S2 \sim \dfrac S2+N-1$ 까지가 원래 들어갈 수들이 있는 노드들이다.
즉, 원래 $A[i]=x$ 라면, 트리에서 $i+\dfrac S2$ 자리에 $x$를 삽입해주고 시작하면 된다.
이제 init 함수 내부에서 리프 노드를 제외하고 아래 달린 노드들부터 자식들의 배열들을 이용해서 Merge Sort과정을 진행해주며 각 정점들의 배열이 자식들의 배열이 정렬되어서 합쳐진 상태를 유지하게끔 해주면 된다.
void init() {
for (int i = size / 2 - 1; i >= 1; i--) {
auto &c = tree[i], &left = tree[i * 2], &right = tree[i * 2 + 1];
c.resize(sz(left) + sz(right));
for (int p = 0, l = 0, r = 0; p < sz(left) + sz(right); p++) {
if (r == sz(right) || (l < sz(left) && left[l] < right[r]))
c[p] = left[l++];
else c[p] = right[r++];
}
}
}
2. 구간에 대해 $K$ 이상의 수 개수 쿼리
세그먼트 트리와 아주 유사하게 진행할 수 있다.
$[l, r]$ 구간에 완전히 현재 노드가 포함될 때, lower_bound 를 이용해 배열의 크기에서 이만큼 빼서 $K$ 이상의 수의 개수를 세주어 반환하는 것을 볼 수 있다.
int _greater_or_equal_than_k(int n, int nl, int nr, int l, int r, int k) {
if (nr < l || nl > r) return 0;
if (nl >= l && nr <= r) return sz(tree[n]) - lbi(tree[n], k);
int m = nl + nr >> 1;
return _greater_or_equal_than_k(n * 2, nl, m, l, r, k) +
_greater_or_equal_than_k(n * 2 + 1, m + 1, nr, l, r, k);
}
int greater_or_equal_than_k(int l, int r, int k) {
return _greater_or_equal_than_k(1, 0, size / 2 - 1, l, r, k);
}
연습 문제
BOJ 13537 - 수열과 쿼리 1
BOJ 7469 - K번째 수
Merge Sort 트리는 그대로 쓰되, 이분 탐색을 이용해서 적절한 $K$를 찾아주면 된다.
즉, 한 쿼리당 시간복잡도는 $O(\log ^3 N)$ 이 소요된다.
BOJ 15899 - 트리의 색깔
Euler Tour Technic 을 써서 트리를 펴준다음에 Merge Sort Tree를 사용해주면 된다.



Comments