Manacher

Manacher 알고리즘은 문자열에서 각 위치에서 좌우로 몇개의 일치하는 문자가 이어지는지 $O(n)$에 검사할 수 있게 해준다.

기본적으로 문자열이 팰린드롬인지 아닌지는 $O(N)$에 검사가 가능하지만, 이걸 이용하면 모든 인덱스에 대해 팰린드롬의 최대 길이를 구할 수 있다.

Manacher는 홀수 길이의 팰린드롬에 동작하는 알고리즘이지만, 추후 살펴볼 문자열의 문자들 사이사이에 더미 문자를 끼워넣어 문자열의 길이를 $2N$으로 만들어주면, 짝수 길이 팰린드롬에 대해서도 검사가 가능하다.

함수 정의

$ret[i]=i$번 째 인덱스에서 좌우로 일치하는 문자들의 최대 길이라고 하자.

예를 들어, $aba$ 라는 문자열에서 $ret[i]=1$ 이다.

그렇다면 $i$를 중앙으로 만들어진 팰린드롬의 길이는 $2ret[i]+1$ 이다.

알고리즘

문자열의 길이가 $n$ 일 때, $i = 0 \to n-1$ 로 진행하며 $ret$를 채울 것이다.

현재 $ret[i]$를 채울 차례라고 한다면, $ret[0] \cdots ret[i-1]$까지 모두 계산이 되어있는 상태일 것이다.

이 때, $0 \sim i-1$ 까지의 인덱스 $j$ 중, $j+ret[j]$ 가 가장 클 때의 $j$를 $p$라 하고 그 때의 $p+ret[p]$를 $r$이라고 하자.

$r$과 $i$의 상대적인 위치가 중요하다.

1. $r<i$

$r<i$ 일 때는 다음과 같은 상황이다.

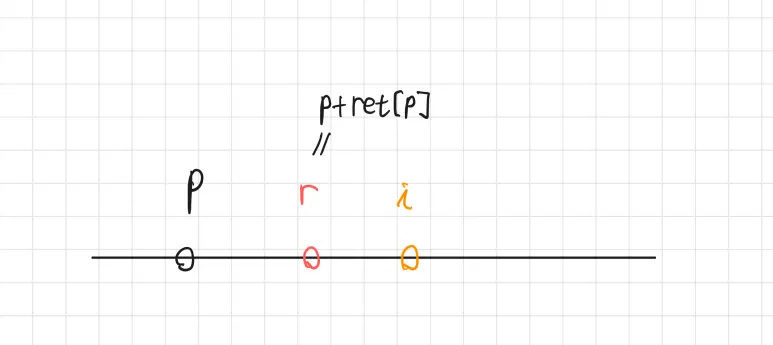
image.png

사실상 $i-1+ret[i-1]$ 은 최소 $i-1$ 이므로 $r<i$ 일 때는 항상 $r=i-1$일 것이다.

이 상황에선 $i$부터 좌우로 직접 검사하며 $ret[i]$를 채워준다.

그러면 $p=i$ 가 될 것이고, $r=i+ret[i]$ 가 될 것이며, 상황은 다음과 같다.

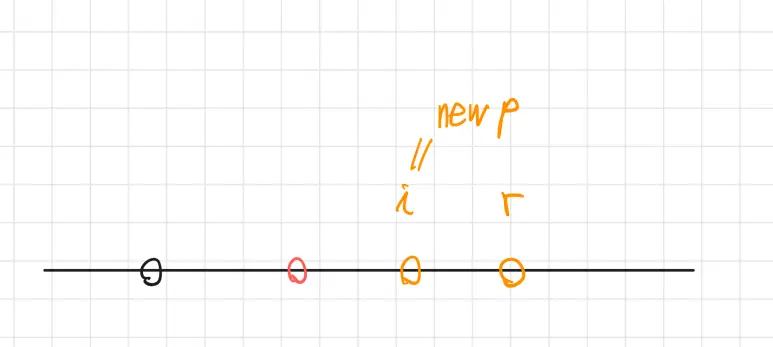
image.png

2. $r \ge i$

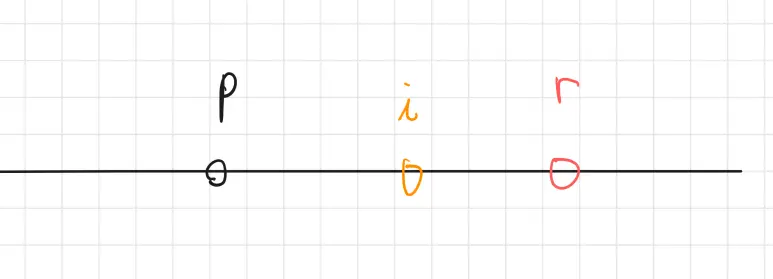
image.png

$r \ge i$

$r=p+ret[p]$ 이므로 우린 $p-ret[p] \sim p+ret[p]$ 구간이 팰린드롬인 것을 안다.

$i’=p \text{에 대한} i$의 대칭점이라고 하자.

$i’=\dfrac {2p-i}{2-1}=2p-i$ 이다. (2:1 외분점)

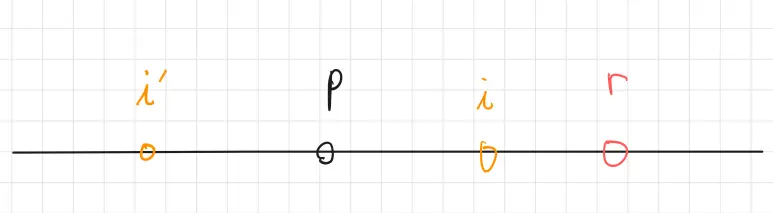
image.png

2-1 $ret[i’]<r-i$ 라면 $ret[i]=ret[i’]$ 이다.

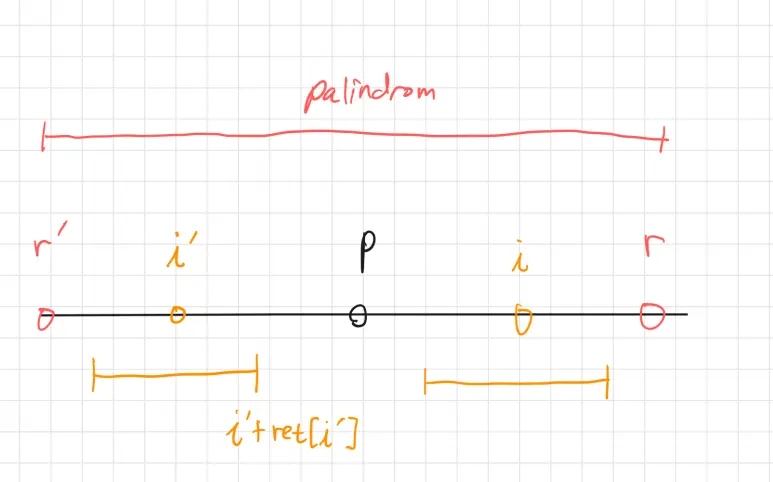
image.png

왜냐면 $i’$ 에서의 제일 긴 팰린드롬이 $p$ 를 기준으로 시작되는 팰린드롬의 구간안에 포함되기 때문에 $i$ 에서의 팰린드롬과 대칭일 것이기 때문이다.

$\Bigl[i’-ret[i’],~i’+ret[i’]\Bigr]$ 구간과 $\Bigl[i-ret[i],~i+ret[i]\Bigr]$ 을 보자.

$$ \begin{aligned} &S_{i'-ret[i']}&=&S_{i+ret[i]}\\ &S_{i'-ret[i']+1}&=&S_{i+ret[i]-1}\\ &&\cdots\\ &S_{i'}&=&S_i\\ &&\cdots \\ &S_{i'-ret[i']-1}&=&S_{i+ret[i]+1}\\ &S_{i'-ret[i']}&=&S_{i+ret[i]}\\ \end{aligned} $$

그렇다 거꾸로 뒤집으면 동일한 구간이기 때문에 $ret[i’]$ 의 길이가 $[r’,\,p]$ 안에 포함이 된다면, 그 길이 자체로 $ret[i]$ 와 같음이 보인다.

2-2 $ret[i’] \ge r-i$ 라면

상황은 다음과 같다. 방금 말한 그 구간을 튀어나간 것이다.

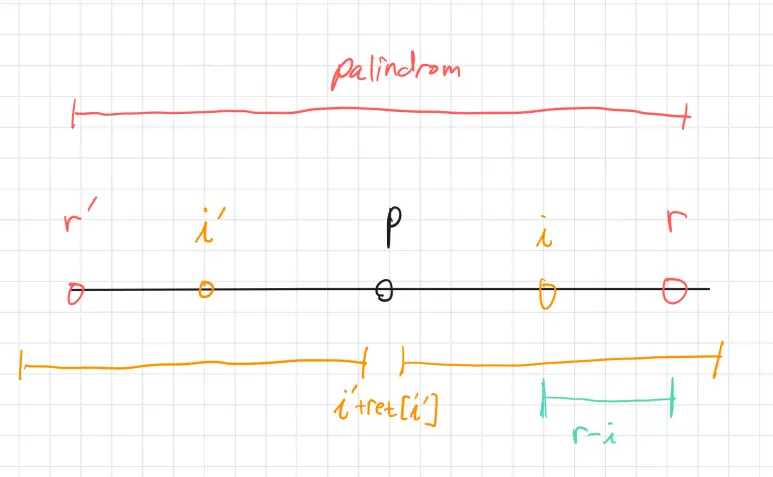
image.png

이제 $i$에서의 팰린드롬 구간이 $r$ 이상으로 벗어나기 때문에 그대로 $ret[i’]$ 를 쓸 순 없다.

따라서 이 경우엔 $ret[i]=r-i$ 로 초기화를 시켜주고 $i+ret[i]+1$ 부터 다시 어디까지 이어지나 검사를 해줄 수 있다.

저렇게 초기화를 시켜줌으로 써, 필요없는 검사를 해줄 필요 없이 우리가 계속 갱신해줘나가야 할 $r$을 늘리는 부분부터 알고리즘을 진행하기 때문에 시간복잡도가 $O(N)$이 되는 핵심이라고 볼 수 있다.

2-1과 2-2를 종합해 보았을 때, 우린 $ret[i]$를 $Min(ret[2p-i], r-i)$ 로 초기화 시켜주면 된다는 결론이 나온다.

구현의 편의성을 위함이다. 밑에 코드를 보면 이해될 것이다.

시간복잡도

$r$이 증가하는 모양새를 보자. $r=i+ret[i]$중 가장 큰 것 이였다.

그렇다면 $r$은 $i+ret[i]$ 이 늘어날 때 같이 늘어난다.

그런데 $i+ret[i]$ 의 최대값은 $N$ 이다.

따라서 시간복잡도는 $O(N)$ 이다.

구현

구현은 짧다.

vi manacher(const string &s) {  
   int n = sz(s), p = 0;  
   vi ret(n);  
  
   for (int i = 1; i < n; i++) {  
      int r = p + ret[p];  
      if (r >= i) ret[i] = min(r - i, ret[2 * p - i]);  
      while (i - ret[i] - 1 >= 0 && s[i - ret[i] - 1] == s[i + ret[i] + 1])  
         ret[i]++;  
      if (i + ret[i] >= r) p = i;  
   }  
  
   return ret;  
}

s[i+ret[i]+1] 과 s[i-ret[i]-i] 를 계속해서 비교해주면서 ret[i] 를 늘려주고 있다.

i+ret[i]+1 이 문자열 범위내인지는 검사하지 않았는데, 어차피 문자열 마지막이 널 문자로 끝나서 괜찮다.
c++언어가 아닌 언어로 구현한다면 꼭 s[i+ret[i]+1] < len(s) 처럼 검사해주자.

짝수 길이의 팰린드롬

홀수 길이일 때 $abbaba$ 라는 문자열이 있다고 하자.

a b b a b a
0 0 0 1 1 0

라는 식으로 $ret$ 배열이 만들어질 것이다.

그럼 홀수 길이의 팰린드롬들은 잘 검사를 했다고 하고, 짝수 길이는 어떻게 할까?

문자열에 포함되지 않는 어떤 더미 문자를 집어넣는 것이다.

꼭 시작과 끝에 더미 문자로 감싸주자.

abbaba $\to$ #a#b#b#a#b#a#

# a # b # b # a # b # a #
0   0   4   0   0   0   0

이렇게 더미 문자들에서의 $ret$ 값이 결국 짝수 팰린드롬의 길이를 의미하게 된다는 것을 알 수 있을 것이다.

홀수 길이에선 팰린드롬의 길이는 $2ret[i]+1$ 라는 것도 기억해주자.

연습 문제

BOJ 13275 - 가장 긴 팰린드롬 부분 문자열

기본 문제이다.

string transform(const string &s) {  
   string ret = "$";  
   for (int i = 0; i < sz(s); i++, ret += '$') ret += s[i];  
   return ret;  
}  
vi manacher(const string &s) {  
   int n = sz(s), p = 0;  
   vi ret(n);  
  
   for (int i = 1; i < n; i++) {  
      int r = p + ret[p];  
      if (r >= i) ret[i] = min(r - i, ret[2 * p - i]);  
      while (i - ret[i] - 1 >= 0 && s[i - ret[i] - 1] == s[i + ret[i] + 1])  
         ret[i]++;  
      if (i + ret[i] >= r) p = i;  
   }  
  
   return ret;  
}  
  
void solve() {  
   string s;  
   cin >> s;  
   vi odd = manacher(s);  
   int ans = 1;  
   for (int i: odd) ans = max(ans, i * 2 + 1);  
   vi even = manacher(transform(s));  
   for (int i = 0; i < sz(even); i += 2) ans = max(ans, even[i]);  
   cout << ans;  
}

BOJ 18171 - ABB

풀이

Comments

You may also enjoy