PrerequisitePermalink

• Dynamic Segment Tree

Li-Chao TreePermalink

리차오트리는 직선의 방정식을 관리하는 세그먼트 트리를 의미하며 다음과 같은 연산이 가능하다.

• 직선 삽입 $O(\log N)$
• $x$ 좌표에 대해서 가장 $f(x)$가 최대거나 최소인 직선 쿼리 $O(\log N)$
• 온라인으로 쿼리를 처리
• 직선 삭제 불가

오프라인 Li-Chao Tree나 Persistent Li-Chao Tree 변형도 존재한다.

사실 위 쿼리는 LineContainer로도 구현 가능하지만, Offline Dynamic Connectivity를 같이 써서 풀려면 리차오 트리를 익혀두는 것이 좋다.

구현Permalink

이 글에선 일반성을 잃지않고 최대값을 구하는 리차오트리를 구현하자.

세그먼트 트리의 노드들은 하나의 직선을 관리하고, 노드의 범위가 $[nl,nr]$ 이라 한다면 그 직선은 $[nl,nr]$ 에서 $f(x)$ 값이 구간 길이 절반 이상에서 최대를 갖는다.

어떤 직선의 방정식 $y=ax+b$ 에 있어 직선을 $(a,b)$로 나타낸다 하자.

처음에는 모든 노드들에 $a=0, b=-\infty$ 같은 기본값을 설정한다.

다음은 직선과 노드를 나타내는 구조체 선언이다.

const int inf = 1e9;  
struct Line {  
   int a, b;  
   int f(int x) { return a * x + b; }  
};  
Line base = {0, -inf};

struct Node {  
   // 왼쪽 자식 번호, 오른쪽 자식 번호
   int l = -1, r = -1;  
   Line line;  
};

업데이트Permalink

Dynamic Segment Tree와 코드가 매우 유사하며 직선은 다음과 같이 추가된다.

처음엔 전체 구간에 대해 $[nl, nr]$ 을 설정하며 직선을 인자로 넘긴다.

void update(int n, int nl, int nr, Line &line) {  
     // ...
}

다음과 같이 구간이 있고, 원래 있던 직선이 빨간색처럼 있다고 하자.

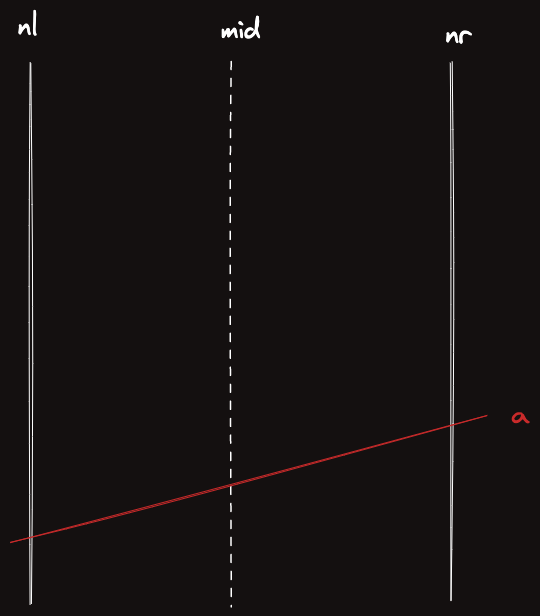
새로운 직선 $b$가 들어왔다고 하자.

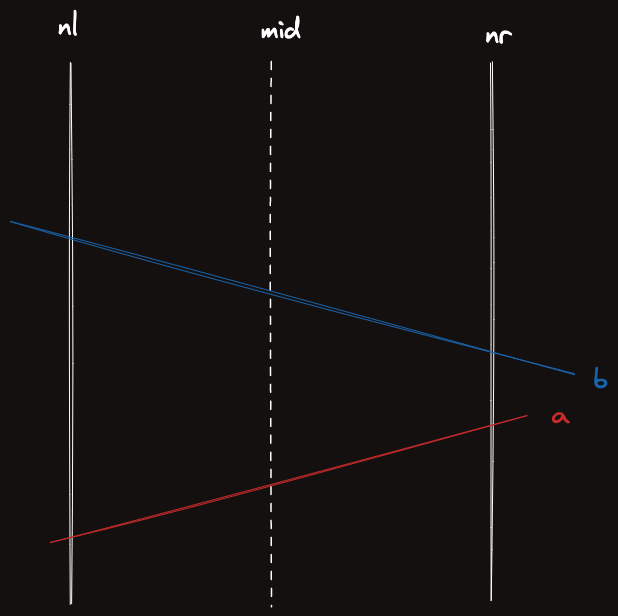
$b$가 위와 같이 $f_b(nl) \ge a,~ f_b(nr) \ge a$ 라면 그냥 이 구간은 $b$로 직선을 교체해주고 재귀호출을 종료한다.

그렇지 않다고 하자.

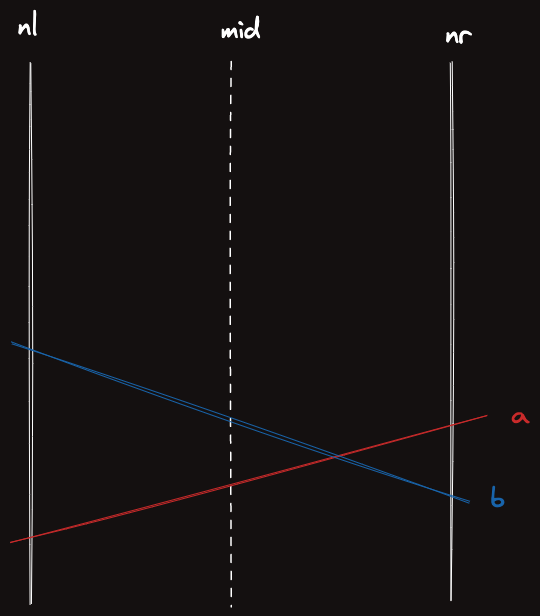
이럴땐 우선 헷갈리지 않게 $f(nl)$ 이 더 큰것을 $b$ 라고 swap 을 하든지 해서 교체한다.

처음에 리차오트리는 구간에서 절반 이상 최대값을 갖는 직선을 가지고 있는다고 했으므로, $f(mid)$ 값을 확인한다.

위처럼 $f_b(mid) \ge f_a(mid)$ 라면 이 구간의 직선은 $b$가 되어야 하고, $(mid, nr]$ 구간에선 $a$ 를 전달하여 업데이트를 진행한다.

위처럼 그렇지 않다면 현재 구간에서의 직선은 $a$가 되어야하고 $[nl, mid)$ 인 구간에 직선 $b$를 전달하여 업데이트를 진행한다.

코드는 다음과 같다.

void update(int n, int nl, int nr, Line line) {  
   Line a = tree[n].line;  
   Line b = line;  
   // b가 nl에서 더 위에 있는 직선이 되게  
   if (a.f(nl) > b.f(nl)) swap(a, b);  
  
   if (b.f(nr) >= a.f(nr)) {  
      tree[n].line = b;  
      return;  
   }  
  
   int mid = nl + (nr - nl) / 2;  
   if (b.f(mid) >= a.f(mid)) {  
      tree[n].line = b;  
      if (tree[n].r == -1) {  
         tree[n].r = tree.size();  
         tree.push_back({});  
      }  
      update(tree[n].r, mid + 1, nr, a);  
   } else {  
      tree[n].line = a;  
      if (tree[n].l == -1) {  
         tree[n].l = tree.size();  
         tree.push_back({});  
      }  
      update(tree[n].l, nl, mid, b);  
   }  
}

점 쿼리Permalink

어떤 $x$에 대해 구간 $[l, r]$ 에서 가장 $f(x)$가 높은 값을 내뱉는 직선을 찾는다고 하자.

쿼리를 하며 $[nl, nr]$ 을 $x$ 까지 좁혀가며 만나는 구간들에서의 직선들의 $f(x)$ 값을 모두 max 연산으로 활용해준다.

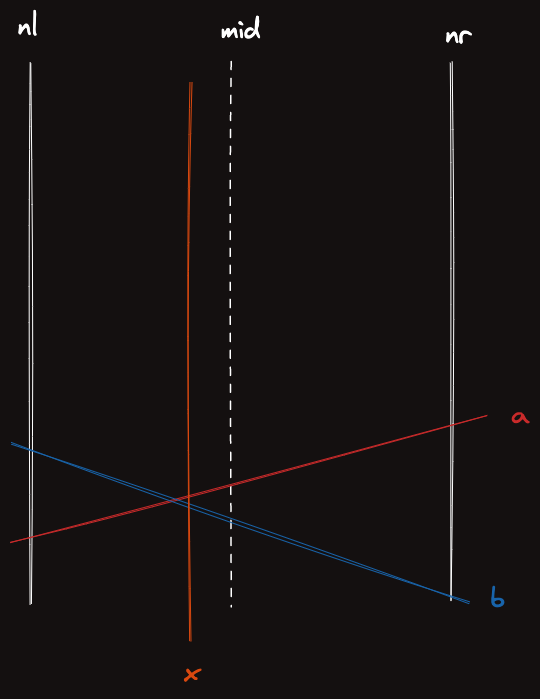
왜냐면 위처럼 구간에서 관리하고 있는 직선은 $a$ 인데, 이제 $[nl, mid)$ 쪽엔 $b$가 전달됐었기 때문에 그쪽에서 최대값이 아닌 $f_a(x)$가 최대값이 나올 것이기 때문이다.

코드는 다음과 같다.

int query(int n, int nl, int nr, int x) {  
   if (n == -1) return -inf;  
   if (nl == nr) {  
      assert(nl == x);  
      return tree[n].line.f(x);  
   }  
   int mid = nl + (nr - nl) / 2;  
   if (x <= mid) return max(tree[n].line.f(x), query(tree[n].l, nl, mid, x));  
   else return max(tree[n].line.f(x), query(tree[n].r, mid + 1, nr, x));  
}

리차오트리 전체 코드는 다음과 같다.

const int inf = 2e25;  
struct Line {  
   int a, b;  
   int f(int x) { return a * x + b; }  
};  
Line base = {0, -inf};  
  
struct Node {  
   int l = -1, r = -1;  
   Line line = base;  
};  
  
struct LiChaoTree {  
   vector<Node> tree;  
   LiChaoTree() {  
      tree.pb({});  
   }  
   void update(int n, int nl, int nr, Line line) {  
      Line a = tree[n].line;  
      Line b = line;  
      // b가 nl에서 더 위에 있는 직선이 되게  
      if (a.f(nl) > b.f(nl)) swap(a, b);  
  
      if (b.f(nr) >= a.f(nr)) {  
         tree[n].line = b;  
         return;  
      }  
  
      int mid = nl + (nr - nl) / 2;  
      if (b.f(mid) >= a.f(mid)) {  
         tree[n].line = b;  
         if (tree[n].r == -1) {  
            tree[n].r = tree.size();  
            tree.push_back({});  
         }  
         update(tree[n].r, mid + 1, nr, a);  
      } else {  
         tree[n].line = a;  
         if (tree[n].l == -1) {  
            tree[n].l = tree.size();  
            tree.push_back({});  
         }  
         update(tree[n].l, nl, mid, b);  
      }  
   }  
   int query(int n, int nl, int nr, int x) {  
      if (n == -1) return -inf;  
      if (nl == nr) {  
         assert(nl == x);  
         return tree[n].line.f(x);  
      }  
      int mid = nl + (nr - nl) / 2;  
      if (x <= mid) return max(tree[n].line.f(x), query(tree[n].l, nl, mid, x));  
      else return max(tree[n].line.f(x), query(tree[n].r, mid + 1, nr, x));  
   }  
};

연습 문제Permalink

여러 Convex Hull Trick 문제들을 리차오트리를 이용해 풀어줄 수 있다.

CHT랑 개념이 굳이 크게 섞이지 않고 리차오트리만을 사용해서 푸는 대표적인 문제는 BOJ 12795 - 반평면 땅따먹기 가 되시겠다.

• 참고
• 참고