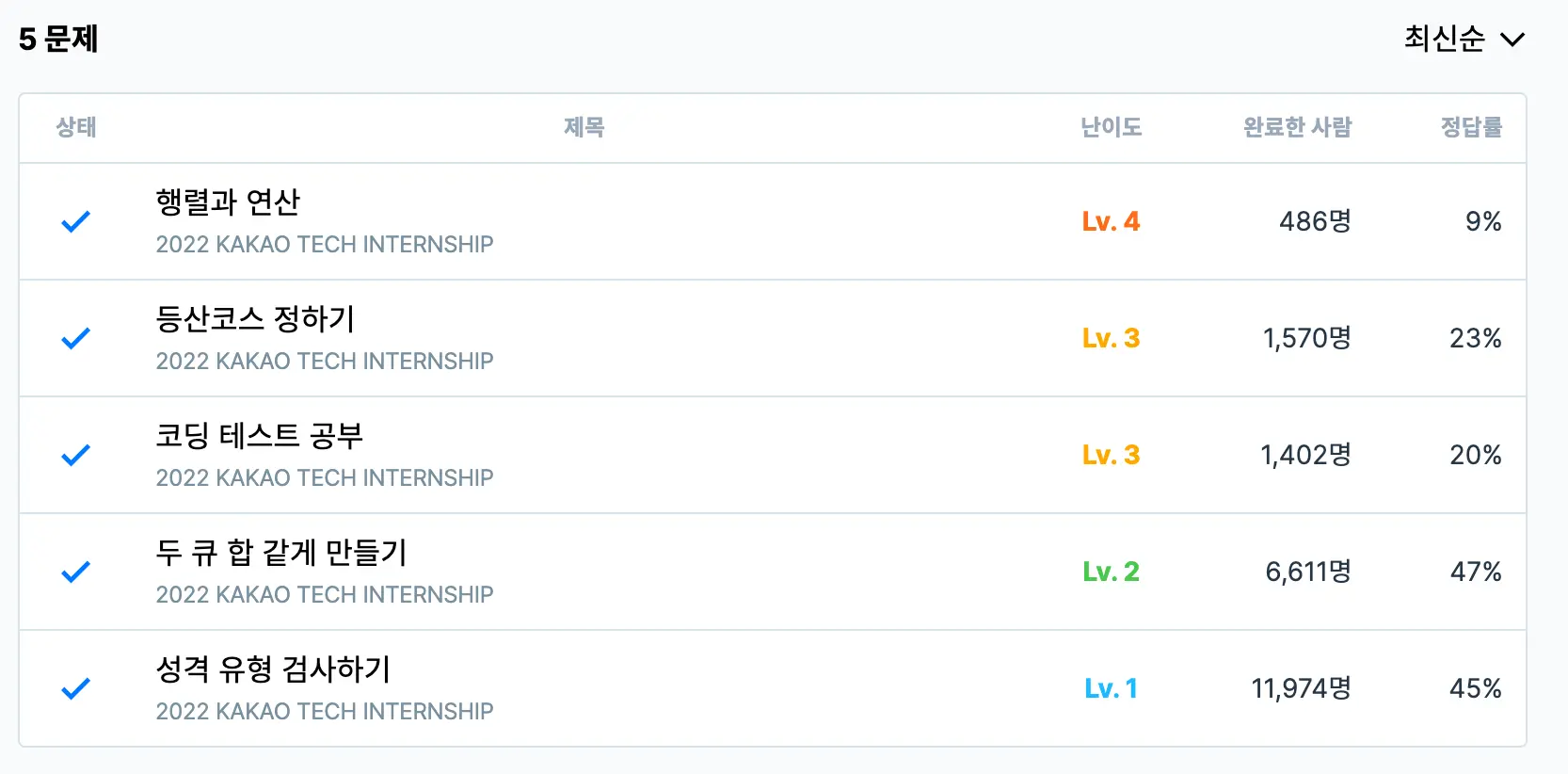
정확히 90분 걸려서 풀었는데, 코테 왜이리 어려워졌을까
1- 성격 유형 검사하기 (0:04)
solved.ac 기준 체감 난이도 - 실버 3
열심히 구현해주자. 1번치고 좀 더 쉬운편
map<char, int> idx{
{'R', 0},
{'T', 1},
{'C', 2},
{'F', 3},
{'J', 4},
{'M', 5},
{'A', 6},
{'N', 7},
};
string solution(vector<string> survey, vector<int> choices) {
int n = sz(survey);
vi a(8);
for (int i = 0; i < n; i++) {
int c = choices[i];
string s = survey[i];
if (c == 1) a[idx[s[0]]] += 3;
if (c == 2) a[idx[s[0]]] += 2;
if (c == 3) a[idx[s[0]]] += 1;
if (c == 5) a[idx[s[1]]] += 1;
if (c == 6) a[idx[s[1]]] += 2;
if (c == 7) a[idx[s[1]]] += 3;
}
string ret;
if (a[0] >= a[1]) ret += 'R';
else ret += 'T';
if (a[2] >= a[3]) ret += 'C';
else ret += 'F';
if (a[4] >= a[5]) ret += 'J';
else ret += 'M';
if (a[6] >= a[7]) ret += 'A';
else ret += 'N';
return ret;
}
2- 두 큐 합 같게 만들기 (0:13)
solved.ac 기준 체감 난이도 - 골드 5
믿음으로 풀면된다.
몇가지 엣지 케이스만 체크해주자.
어차피 정답이 되는 연속된 구간이 있다면 큰곳에서 작은곳으로 옮겨줌으로써 정답이 나오게 된다.
ll solution(vector<int> queue1, vector<int> queue2) {
int n = sz(queue1);
ll sum = acc(queue1) + acc(queue2);
if (sum % 2) return -1;
if (acc(queue1) == acc(queue2)) return 0;
ll sum1 = acc(queue1);
ll sum2 = acc(queue2);
ll k = sum / 2;
if (maxe(queue1) > k || maxe(queue2) > k) return -1;
int ans = 0;
queue<int> q1, q2;
for (int i: queue1) q1.push(i);
for (int i: queue2) q2.push(i);
while (sum1 != sum2) {
if (ans > n * 3) return -1;
if (sum1 > sum2) {
sum1 -= q1.front();
sum2 += q1.front();
q2.push(q1.front());
q1.pop();
} else {
sum2 -= q2.front();
sum1 += q2.front();
q1.push(q2.front());
q2.pop();
}
ans++;
}
return ans;
}
3- 코딩 테스트 공부 (0:52)
solved.ac 기준 체감 난이도 - 골드 3
함정카드가 있어 멸망했다.
처음에 BFS로 걍 생각없이 하다가 안되는거알고 반복문 dp로 돌리다가 반복문 dp가 아닌 재귀로 짜야하는걸 깨닫느라 시간도 오래걸렸다.
게다가 또 말린 부분은 왜 자꾸 MAX 제한을 더 크게줘야 테케가 통과하지를 생각해보니 (150, 1) 같이 보상이 주어지고 뒤에 1을 계속 써야하는 경우에 (150) 이 계속 증가해서 올바른 값을 구해주지 않는다는 것이였다.
따라서 a,c가 있을 때, 계속 최대값을 넘어간다면 최대값으로 제한해주는 테크닉이 필요했고, 이 문제들 중에서 가장 배울게 있었던 문제이다.
그리고 이 문제에 효율성이 시간제한이 뭔가 왜 안돌지 하게 걸려있기도 한데, 프로그래머스에서 문제를 만들어본 입장에서 시간을 제한하는게 아니라 샘플 코드의 배수로 시간을 제한하다보니 불편한점이 있어 그럴것같기도 하다.
const int MAX = 190;
int solution(int alp, int cop, vector<vector<int>> problems) {
problems.pb({0, 0, 1, 0, 1});
problems.pb({0, 0, 0, 1, 1});
int a_req_mx = 0, c_req_mx = 0;
for (const auto &to: problems) {
int a_req = to[0], c_req = to[1], a_rwd = to[2], c_rwd = to[3], cost = to[4];
a_req_mx = max(a_req_mx, a_req);
c_req_mx = max(c_req_mx, c_req);
}
vvi dp(MAX + 1, vi(MAX + 1, -1));
function<int(int, int)> fn = [&](int a, int c) -> int {
a = min(a, MAX);
c = min(c, MAX);
if (a >= a_req_mx && c >= c_req_mx) return 0;
int &ret = dp[a][c];
if (~ret) return ret;
ret = 1e9;
for (const auto &to: problems) {
int a_req = to[0], c_req = to[1], a_rwd = to[2], c_rwd = to[3], cost = to[4];
if (a_rwd == 0 && c_rwd == 0) continue;
if (a_req > a || c_req > c) continue;
ret = min(ret, cost + fn(a + a_rwd, c + c_rwd));
}
return ret;
};
int ret = fn(alp, cop);
assert(ret != 1e9);
return ret;
}
4- 등산코스 정하기 (1:07)
solved.ac 기준 체감 난이도 - 골드 2
그냥 정상들부터 BFS를 돌려서 각 값들을 <지나온 간선의 최소 가중치, 정상인 시작점> pair의 최소값으로 계속 갱신해주면 답이 바로 구해진다.
vector<int> solution(int n, vector<vector<int>> paths, vector<int> starts, vector<int> tops) {
vector<vector<pi>> edges(n);
for (auto &v: paths) {
v[0]--;
v[1]--;
edges[v[0]].pb({v[1], v[2]});
edges[v[1]].pb({v[0], v[2]});
}
for (int &i: starts)i--;
for (int &i: tops)i--;
vector<pi> dp(n, {1e9, 1e9});
queue<int> q;
for (int t: tops) {
dp[t] = {0, t};
q.push(t);
}
while (sz(q)) {
int cur = q.front();
q.pop();
for (auto &[to, w]: edges[cur]) {
int nxt_w = max(dp[cur].fi, w);
pi nxt = {nxt_w, dp[cur].se};
if (dp[to] > nxt) {
dp[to] = nxt;
q.push(to);
}
}
}
int min_w = 1e9;
for (int s: starts) {
min_w = min(min_w, dp[s].fi);
}
int ans = 1e9;
for (int s: starts) {
if (dp[s].fi == min_w) {
ans = min(ans, dp[s].se + 1);
}
}
return {ans, min_w};
}
5- 행렬과 연산 (1:30)
solved.ac 기준 체감 난이도 - 플레티넘 5
풀이는 금방 떠올렸는데, 구현이 좀 걸렸다.
shift는 y offset을 변경해주는 것으로 처리하고, 회전은 좀 까다롭다.
모든걸 deque 로 바꾼 다음에, 0, X−1 번 column은 따로 처리해줘야한다.
네개의 덱을 회전시키는듯하게 구현하면 된다.
오프셋 관리도 좀 헷갈리는데, 쉬프트될때마다 각 가로줄의 맨 왼쪽 오른쪽친구들도 바꿔줌을 잊지말자.
여기서 좀 헤맸다.
vector<vector<int>> solution(vector<vector<int>> original, vector<string> op) {
int Y = sz(original), X = sz(original[0]);
int y_offset = 0;
vector<deque<int>> b(Y);
deque<int> col1, col2;
for (int y = 0; y < Y; y++) for (int i: original[y]) b[y].pb(i);
for (int y = 0; y < Y; y++) {
col1.pb(original[y][0]);
col2.pb(original[y][X - 1]);
}
for (string o: op) {
if (o[0] == 'R') {
int y1 = y_offset;
int y2 = md(Y, y_offset - 1);
b[y1][0] = col1[0];
b[y1][X - 1] = col2[0];
b[y2][0] = col1[Y - 1];
b[y2][X - 1] = col2[Y - 1];
col1.pop_front();
b[y1].push_front(col1.front());
b[y1].pop_back();
col2.push_front(b[y1].back());
col2.pop_back();
b[y2].push_back(col2.back());
b[y2].pop_front();
col1.push_back(b[y2].front());
} else {
y_offset = md(Y, y_offset - 1);
int y1 = y_offset;
int y2 = md(Y, y_offset - 1);
col1.push_front(col1.back());
col1.pop_back();
col2.push_front(col2.back());
col2.pop_back();
}
}
vvi ans(Y, vi(X));
for (int y = 0; y < Y; y++) {
for (int x = 0; x < X; x++) {
if (x == 0) {
ans[y][x] = col1[y];
} else if (x == X - 1) {
ans[y][x] = col2[y];
} else {
int yy = md(Y, y + y_offset);
ans[y][x] = b[yy][x];
}
}
}
return ans;
}



Comments