2024 카카오 겨울 인턴십 코딩테스트 해설 - Python
프로그래머스에서 문제를 풀어보도록 하자.
총 $5$문제로, $5$시간을 보았다고 한다. 심심해서 해설을 작성한다.
2. 도넛과 막대 그래프
전처리
프로그래머스에서 중요한 것은 입력이 들어오는 형태가 문제를 풀기에 적합할 수 있지 않으므로 자신이 원하는 방법으로 데이터를 정재하는 과정이 필요할 수 있다는 것이다.
이 문제는 정점의 수 $n$을 입력으로 주지도 않고 간선의 형태도 쓸모없게 들어오므로 BFS를 돌리기 쉬운 형태로 인접리스트로 바꿔주는 과정을 거쳐주자.
def solution(edges_input):
# 정점의 개수 n 찾기
n = 0
for [u, v] in edges_input:
n = max(n, u, v)
# 인접 리스트로 관리하기 쉽게 옮겨담기
edges = [[] for _ in range(n + 1)]
for [u, v] in edges_input:
edges[u].append(v)
solution함수의 입력이 원래 edges라는 이름을 가졌는데, 이걸 데이터를 정재한 후 안쓰고 자기가 쓰려는 변수 이름과 겹친다면 edges_input과 같이 바꾸고 새로 만들 인접리스트를 edges 라는 이름으로 바꿔주는 것도 가능하다.
아이디어
입력과 출력을 보자. 우리는 도넛, 막대, 8자 모양 그래프의 개수를 세고 어떤 노드가 추가되었는지를 파악해야 한다.
그리고 입력의 개수를 보자. 간선이 $1,000,000$개라는 것은 웬만하면 정점도 $10^5 \sim 10^6$ 개라는 것이고 $O(N^2)$ 정도의 알고리즘은 쓸 수 없고 일반적인 $O(V+E)$나 로그가 하나 더 붙은 알고리즘정도로 해결해야 된다는 것을 의미한다.
문제를 단순하게 생각해서 새로 추가된 정점이 없고 연결된 그래프가 하나라고 하자. 즉, 하나의 도넛 그래프나 막대 그래프나 8자 그래프가 있는 입력이 주어진다고 해보자.
이 때 각 그래프를 구분하는 방법은 다음과 같다. $V$가 정점의 개수 $E$가 간선의 개수라고 한다면,
- 도넛 그래프: $V=E$
- 막대 그래프: $V=E+1$
- 8자 그래프: $V=E-1$
이제 사고를 확장해서 새로 추가된 정점이 없는 채 그래프(연결 컴포넌트)가 여러개가 같이 있다고 하자.
BFS와 방문 되었는지 여부 배열을 통해 방문되지 않은 정점을 만났을 때 쭉 그래프를 순회하면 하나의 연결 컴포넌트를 순회할 수 있으므로 개별적으로 처리해주면 된다.
이제 새로 정점을 추가한다고 해보자.
여기서 in-degree와 out-degree의 개념이 나오는데, in-degree는 어떤 정점에서 자신에게 들어오는 간선 수, out-degree는 자신에서 나가는 간선 수이다.
이는 유향 그래프에서만 존재하는 개념이다.
새로 추가된 정점은 in-degree가 $0$이다. 자신에게 들어오는게 하나도 없다.
out-degree는 문제의 제한사항을 잘 읽으면 항상 $2$ 이상임이 보장된다. 왜냐면 각 그래프 타입의 합이 최소 $2$개 이상이라고 적혀있기 때문이다.
이제 in-degree가 $0$이고 out-degree가 $2$ 이상인 정점은 항상 추가된 정점인지를 고려해보자.
도넛 그래프나 8자 그래프의 모든 정점은 in-degree가 $0$이 아니기 때문에 항상 제외되고, 막대 그래프에서는 하나의 끝에있는 정점이 in-degree가 $0$이 된다.
그러나 그 정점도 out-degree는 $1$이므로 위의 조건을 만족하는 정점이 새로 추가되는 정점임이 항상 보장된다.
따라서 우리는 새롭게 추가되는 정점을 이걸 이용해서 찾고 그 정점에서 뻗어나간 각 그래프의 정점들에서 BFS를 이용해 각 연결 컴포넌트(새로 추가된 정점은 제외된) 의 $V, E$를 세서 판단할 수 있다.
전체 코드
3. 주사위 고르기
아이디어
$n$은 최대 $10$이므로 가질 수 있는 주사위의 조합은 최대 $10$개 중에 $5$개를 고르는 $_{10}~\text{C}~_5=252$ 이다. 따라서 우리가 무슨 알고리즘을 쓰든 시간 복잡도는 $O(252 \cdot ?)$ 이다.
여기서 더 나아가면 $[1,2,3,4,5], [6,7,8,9,10]$ 과 $[6,7,8,9,10],[1,2,3,4,5]$ 를 고르는 것은 동일하므로 $\dfrac{252}{2}$ 번만 해주면 되지만, 딱히 시간을 최적화하지 않는 한 필요없다.
그렇게 주사위를 $\dfrac{n}{2}$개 골랐다고 해보자.
$\dfrac{n}{2}$ 개의 주사위가 각각 어떤 수가 나오냐에 따라 총 합이 달라지고, 주사위는 항상 $6$면이 있고 각 수는 $1 \le x \le 100$ 이므로 $n=10$ 이여서 주사위가 $5$개가 된다고 해도 주사위의 합은 $1 \le S \le 500$ 이 될 것이다.
각각 나올 수 있는 주사위의 경우의 수는 $n=10$ 가지라고 하면 $6^{10}$ 가지이며 $252$에 이를 곱하면 $150$억번정도로 시간초과나기 딱좋다.
핵심 아이디어는 한 명이 던진 주사위와 다른 한 명이 던진 주사위의 경우의 수를 같이 세줄 필요가 없다는 것이다.
| 주사위의 합 | 1 | 2 | 3 | … | 500 |
|---|---|---|---|---|---|
| 나 | x | y | z | … | |
| 상대방 | a | b | c | … |
이런식으로 주사위의 합에 대한 테이블이 있다고 하면
이 테이블을 채우는데 필요한 시간복잡도는 $O(6^{\frac{n}{2}})$이다. 즉, $n=10$ 일 때, $6^5$이다.
면이 $6$개인 주사위를 총 $\dfrac{n}{2}$ 번 굴리기 때문에 $\displaystyle _{6}~\Pi~ _{\text{주사위의 수}}$ 이고, 이건 재귀함수를 이용해 경우의 수를 모두 셀 수 있다.
내가 이기는 경우의 총 합은 $x(0) + y(a) + z(a+b) + \cdots$ 처럼 계산될 수 있다.
테이블을 가지고 내가 이기는 경우를 세는건 $O(500^2)$ 면 된다.
최종 시간복잡도는 $O(252 \left( 6^{\frac{n}{2}} + 500^2 \right))$ 가 되고 이는 $n=10$ 인 경우에도 $1$억보다 작으므로 충분히 통과한다.
여기서 $O(500^2)$ 부분은 구간합 배열이나 투포인터를 이용하면 $O(500)$으로 처리될 수 있지만 필요하지 않은 문제이다.
코드
아이디어는 알아도 코드를 짜는데 필요한 테크닉들이 좀 있다.
$n$ 개의 주사위 중 $\dfrac{n}{2}$개를 고르는건 $N,M$ 시리즈처럼 재귀함수를 써도 되고 비트마스크를 써도 된다.
주사위가 $4$개라면 $0000(0) \sim 1111(15)$ 까지 반복해보며 비트가 $1$인 부분과 $0$인 부분으로 주사위가 나뉘어 졌다고 생각한다.
$1010$이나 $0011$같이 비트 수가 $2$ 개일 때만 $2$개씩 주사위가 제대로 골라진 것으로 하여 진행하고 각 배열에 담는다.
def solution(dice):
n = len(dice)
max_win_count = 0
max_win_dice_set = []
for bit in range(0, (1 << n)):
bit_count = bin(bit).count('1')
if bit_count != n / 2:
continue
left_dices, right_dices = [], []
for i in range(n):
if (1 << i) & bit:
left_dices.append(i)
else:
right_dices.append(i)
이러면 $_{n} \text{C} _{n/2}$ 가지수에 대해서 처리를 할 준비가 된 것이다.
이제 테이블을 재귀함수로 채운다.
left_sum, right_sum = [0] * 501, [0] * 501
sum = 0
def calculate_dice_sum(i, is_left, dice_set):
nonlocal sum
if i == n / 2:
if is_left:
left_sum[sum] += 1
else:
right_sum[sum] += 1
return
for j in range(6):
sum += dice[dice_set[i]][j]
calculate_dice_sum(i + 1, is_left, dice_set)
sum -= dice[dice_set[i]][j]
calculate_dice_sum(0, True, left_dices)
calculate_dice_sum(0, False, right_dices)
sum 이란 변수를 계속 더하고 빼주며 최종적으로 $n/2$ 개의 주사위를 모두 던졌을 때 나올 수 있는 합을 left_sum 이나 right_sum 에 담아준다.
하나의 함수를 재사용하기 위해 이게 is_left 인지와 현재 주사위 조합을 인자로 넘긴다.
마지막으로 현재 경우에서 테이블을 갖고 $O(500^2)$ 만큼 순회하며 몇 번을 이길 수 있는지 확인하고 현재 기록된 정답보다 크다면 정답을 업데이트한다.
win = 0
for left in range(1, 501):
for right in range(1, left):
win += left_sum[left] * right_sum[right]
if win > max_win_count:
max_win_count = win
max_win_dice_set = left_dices
전체 코드
4. n + 1 카드게임
아이디어
전형적인 그리디 문제인데, 중요한 핵심 아이디어는 다음과 같다.
보통 그리디 알고리즘이라 한다면 어떤 경우에서 현재 할 수 있는 최선의 선택을 수행하면 최적의 결과에 도달한다. 라고 배우는 경우가 있는데, 어느정도 맞는 말이지만 이런 문제를 풀 땐 바로 현재 할 수 있는 최선의 선택을 알 수 없다.
이 문제는 선택할 수 있는 선택지들을 계속 모아두고 이제 더 이상 선택을 미룰 수 없을 때 지금까지 모아둔 선택지중에 가장 이득이 되는 것을 고르는 방식으로 해결해야한다.
처음에 $\dfrac{n}{3}$ 개의 카드를 먼저 얻어두었다. 이 중 벌써 합쳐서 $n+1$ 이 되는 것을 pair 라는 변수라고 하자. $n=12$ 이고 $1,3,12,10$ 이 있었다면 $(1,12), (3,10)$ 두 쌍을 벌써 가진 것이므로 pair=2로 시작한다.
문제에서는 다음 라운드로 넘어가기 위해 당장 코인을 써서 카드를 얻거나 버리거나를 결정해야 하는것처럼 보이지만, 당장 다음 라운드로 넘어갈 수 있는 pair라는 값이 남아있다면 일단 이걸 써서 다음 라운드로 넘어간다.
그러고나서 나중에 현재 라운드에서 이전 봤던 카드들을 코인을 써서 지금 얻는걸로 해도 된다. 어떻게 보면 이렇게 넘긴 라운드는 그 카드들을 코인을 써서 언제든지 다시 얻을 수 있는 기회를 얻은 것과 같다.
지금까지 넘겨온 라운드 중 두개가 합쳐서 $n+1$ 가 되는 카드 한 쌍이 있었다면 현재 내가 pair가 다떨어졌을 때 코인 $2$개가 있다면 그걸 과거에 얻었던 걸로 치고 지금 사용하는 것으로 보아도 무방하다.
하지만 항상 pair가 있다면 코인을 안쓰고 남은 pair를 소모하는게 이득이다.
pair가 없다면 코인을 $2$개 소모하는 것보다 원래 처음에 가지고 있었던 $\dfrac{n}{3}$개의 카드중에 이미 가지고 있는 카드가 있을 때 내가 지나쳐온 카드들 중에서 그것과 합쳐 $n+1$이 되는 카드를 코인 $1$개만 소모해서 이번 라운드를 넘기는게 이득이다.
코드
have, seen, pair(zero_coin), one_coin, two_coin, coin 과 같은 변수들을 관리한다.
순서대로 ($n/3$ 개에서 이미) 수를 가지고 있는지 여부, 이전 라운드에 지나쳤는지 여부, 코인 $0,1,2$ 개로 넘길 수 있는지 여부, 현재 코인 개수이다.
전체 코드
5. 산 모양 타일링
단순한 타일 채우기 DP에서 조금 형태만 변한 문제이다.
아이디어
아래 $n+1$ 칸을 기준으로 인덱스가 $0 \sim n$ 까지 $n+1$ 칸이 있다고 설정하면 tops 변수와도 딱 맞게 삼각형이 어디에 존재하는지 맞아떨어진다.
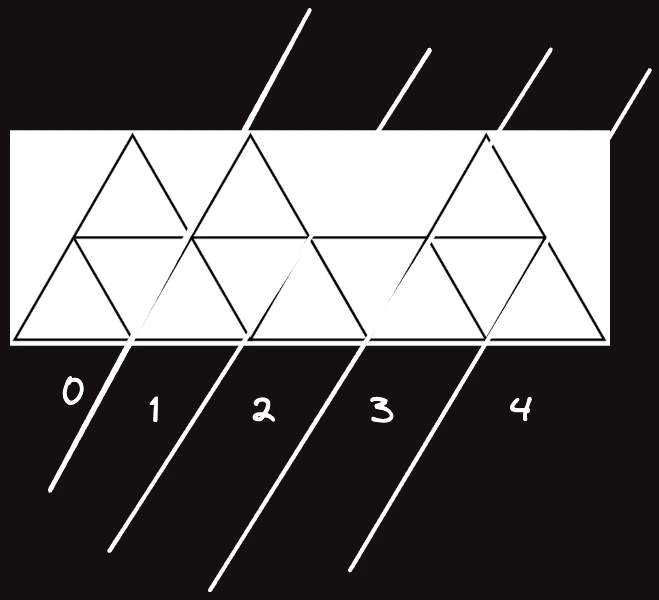
보통 $dp[i]$ 를 $i$ 번 째 칸 직전까지 채우는 경우의 수라고 두는데, 이 문제는 두 가지로 나뉘어야 된다.
- $dp[i][0]$를 $i$번 째 직전까지 채우며 $i$ 번 째 칸의 젤 밑 삼각형을 채우지 않는 경우의 수
- $dp[i][1]$를 $i$번 째 직전까지 채우며 $i$ 번 째 칸의 젤 밑 삼각형까지 이전 칸에서 넘어온 두 칸짜리로 채우는 경우의 수
라고 하자.
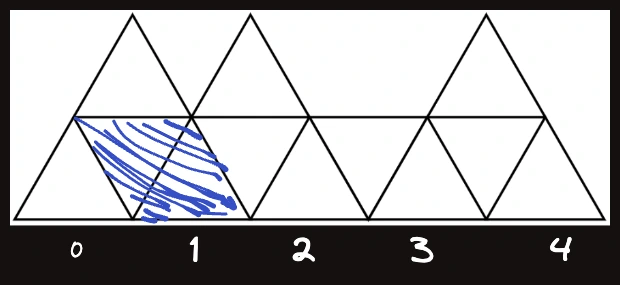
$dp[1][1]$ 같은 경우엔 위처럼 현재 $1$ 열을 보고 있는데 젤 밑 삼각형까지 이전 열에서 두 칸 짜리로 채워서 넘어온 경우이다.
dp[i][1]
$dp[i][1]$ 를 채우려면 항상 저 뉘여진 마름모를 써야하는데 그러면 위에 삼각형이 달려있든 말든 저 뉘여진 마름모를 두고 이전열의 나머지는 이전열의 가장 아래 정삼각형이 채워져있던 말든 나머지를 모두 정삼각형으로 채워야 한다.
따라서 경우의 수는 이전 열들의 경우의 수를 모두 더한것이 된다.
즉, $dp[i+1][1]=dp[i][0] + dp[i][1]$ 이다.
dp[i][0]
$dp[i][0]$ 를 채울 때는 삼각형의 여부가 경우의 수에 영향을 미친다. 저것으로 인해 위로 세워진 마름모를 넣거나, 정삼각형 두개로 채우거나 두 가지 경우가 생긴다.
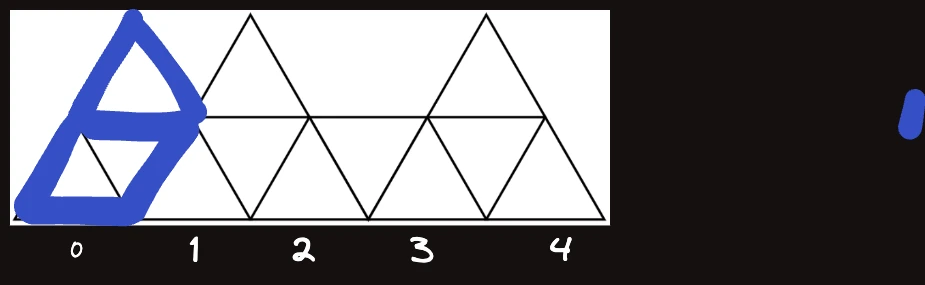
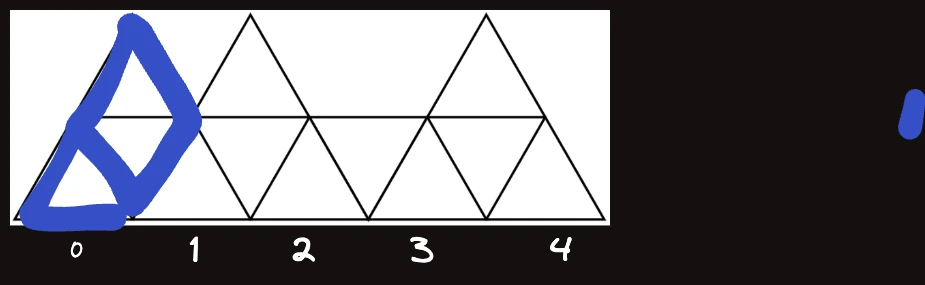
$dp[i-1][0]$ 이 위에 삼각형이 있을 때 $dp[i][0]$에 어떻게 기여하는지 보면 아래와 같이 총 세 가지 경우이다. $i-1$ 번째의 가장 아래쪽 삼각형도 안채워진 상태이다.
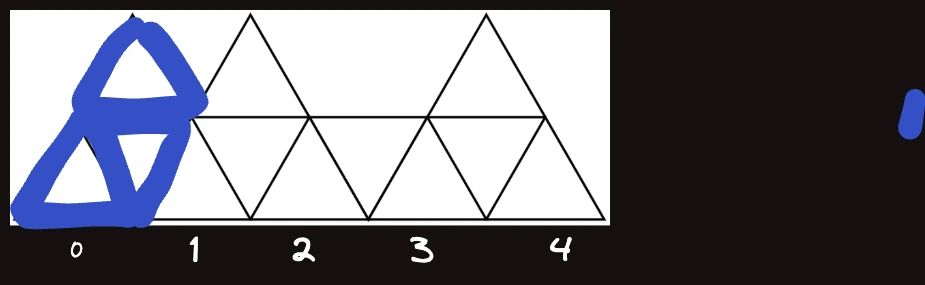
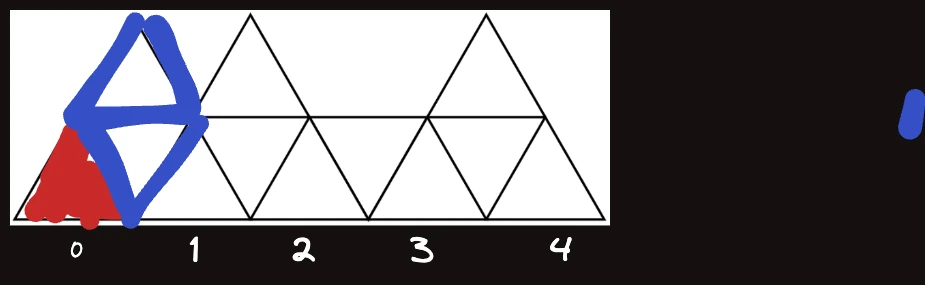
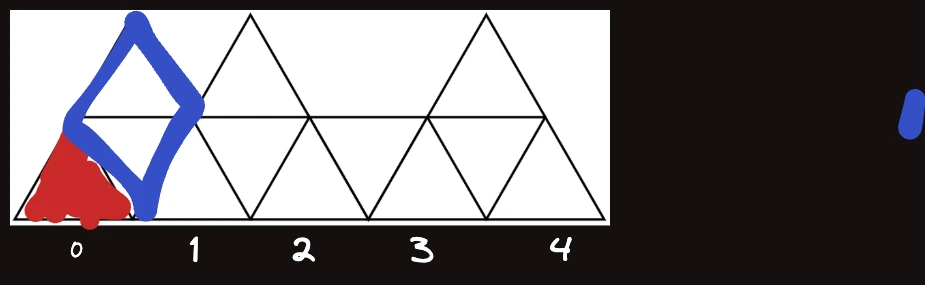
$dp[i-1][1]$ 이 위에 삼각형이 있을 때 $dp[i][0]$에 어떻게 기여하는지 보면 아래와 같이 총 두 가지 경우이다. $i-1$ 번째의 가장 아래쪽 삼각형은 채워진 상태이다.
이제 삼각형이 없을때도 비슷하게 $2, 1$ 가지 경우가 나오므로 점화식을 채워주면 된다.
마지막 정답은 $dp[n][0] + dp[n][1]$ 인데, $dp[n][0]$은 $n$ 번째 칸을 채울 차례이고 아래 삼각형이 채워져있지 않은 상태이므로 그냥 정삼각형 하나를 두개 되는 경우 하나일 것이고, $dp[n][1]$은 $n$ 번째 칸을 채울 차례인데 아래 삼각형이 채워져있으므로 이미 끝난 상태이므로 또 하나이기 때문이다.
Comments