Network Flow 1 - Ford-Fullkerson & Edmonds-Karp
Network Flow
flow알고리즘이라고도 하고 유량 알고리즘이라고도 한다.
PS에서의 flow는 대개 최대 유량(Maximum Flow)을 찾는 문제부터 시작된다.
최대 유량이란 그래프에서 $source$(시작점)과 $sink$(끝 점)이 있을 때, 각 간선이 흐를 수 있는 용량을 가지고 있을 때, $source \to sink$ 로 얼마나 많은 유량을 흘려보낼 수 있냐를 구하는 문제이다.
$source$만 유량을 발생시키고, 다른 정점들은 자신이 받은 유량만큼만 흘려보낼 수 있다.
그걸 찾아서 어따쓸건데? 라는 생각이 들 수 있지만, 최대 유량을 찾는 문제는 정말 많은 유형의 문제에서 최대 유량을 찾는 문제로 치환되어 그래프를 모델링하고 풀 수 있다.
또한 Maximum Flow만 풀어야 할 문제가 아니고 Minimum Cost Maximum Flow(MCMF) 라든지, Minimum Cut 이라든지, 그냥 그 성질 자체를 물어보는 문제들도 있다.
여러가지 알고리즘이 있고 여러가지 정리가 있지만, 일반적인 수준에서는 수십가지의 알고리즘을 알고 있어야 할 필요는 없다.
하지만 Flow를 이해하는데 있어 필수적으로 알아야 할 개념들이 있고, 문제 유형들이 있다.
내용이 방대해서 여러개의 포스팅으로 정리를 해보려 한다.
이전엔 다른 블로그들에서 공부를 하고 기계처럼 알고리즘과 시간복잡도나 정리들을 외워 문제를 해결했다면, 좀 더 체계적으로 어떤 것들이 있는지 살펴보며 정리를 해보려 한다.
Flow 그래프의 성질
1. 간선은 자신의 용량보다 많은 유량을 흘릴 수 없다.
$u \to v$ 간선이 있고, $c[u][v]$ 를 $u \to v$ 로 가는 간선이 가진 용량(capacity)이라고 하고 $f[u][v]$ 를 $u \to v$ 로 흐르는 유량(flow)라고 하자.
$f[u][v] \le c[u][v]$ 를 만족하여야 한다.
2. Source와 Sink를 제외한 정점은 들어오는 유량과 나가는 유량이 동일하다.
$v \in V \setminus \{ source,\,sink \}$ 인 모든 $v$ 에 대해서 $\sum_{(x,v)} f[x][v]=\sum_{(v,x)} f[v][x]$ 이다.
3. 어떤 간선에 흐르는 유량만큼 반대 방향으로는 음의 유량이 흐른다.
$f[u][v]=k$ 일 때, $f[v][u]=-k$ 이다.
음의 유량이 흐른다는게 직관적으로 받아들이긴 어렵지만, 그렇다.
Flow 그래프의 일반성
Flow 그래프는 몇가지 제약을 두고도 기존의 그래프와 일반성을 잃지않고 동일하게 다룰 수 있다.
이러한 것을 이용해 (1)실제 그래프를 단순화하거나, 아니면 (2)구현할 때 고려를 안해도 잘 작동한다든가 식으로 써줄 수 있다.
1. 루프(loop)가 없다
루프는 자기 자신에서 시작해 자기 자신으로 다시 돌아오는데, 유량이 자신에서 시작해서 자신으로 돌아오는 것은 결국 네트워크의 의미로 보자면 아무런 의미를 갖지 않는다.
2. 평행 간선(parallel edge)이 없다
$u \to v$ 로의 간선이 두개가 있고 각각의 용량이 $c_1, c_2$ 라면 간선을 하나로 합쳐주고 그 용량을 $c_1+c_2$ 로 생각해주어도 문제없다.
기존의 그래프에서 흐르던 유량이 새로운 그래프에서도 정확히 동일하게 흐를 수 있다는 것이 보이기 때문이다.
3. 역평행 간선(anti-parallel edge)이 없다.
$u \to v$ 로의 간선이 있고 $v \to u$ 로의 간선이 존재하면 이를 역평행 간선이라 부른다.
$v \to u$ 으로의 용량 $c_2$ 에대해 더미 정점 $w$를 추가해 $v \to w$에도 $c_2$의 용량과 $w \to u$ 에도 $c_2$ 의 용량을 두어 처리한다면 역평행 간선을 없애며 네트워크를 구하는데 동일한 동작을 하는 새로운 그래프를 만들 수 있으므로 플로우 그래프에선 역평행 간선이 존재하지 않는다고 가정할 수 있다.
Ford-Fullkerson
가장 직관적인 포드-폴커슨 알고리즘이 동작하는 방식의 예시를 먼저 보자.
포드-폴커슨 알고리즘은 명백히 시간복잡도가 에드몬드-카프 알고리즘에 비해 최악의 경우에 느리기 때문에 PS에서 쓸일은 없지만 에드몬드-카프 알고리즘이 포드-폴커슨 알고리즘을 개선한 구현이기 때문에 여기서 예시를 들고감이 적절하다.
다음과 같은 그래프를 보자. 파란색으로 쓴 글씨는 (flow/capacity) 이다.
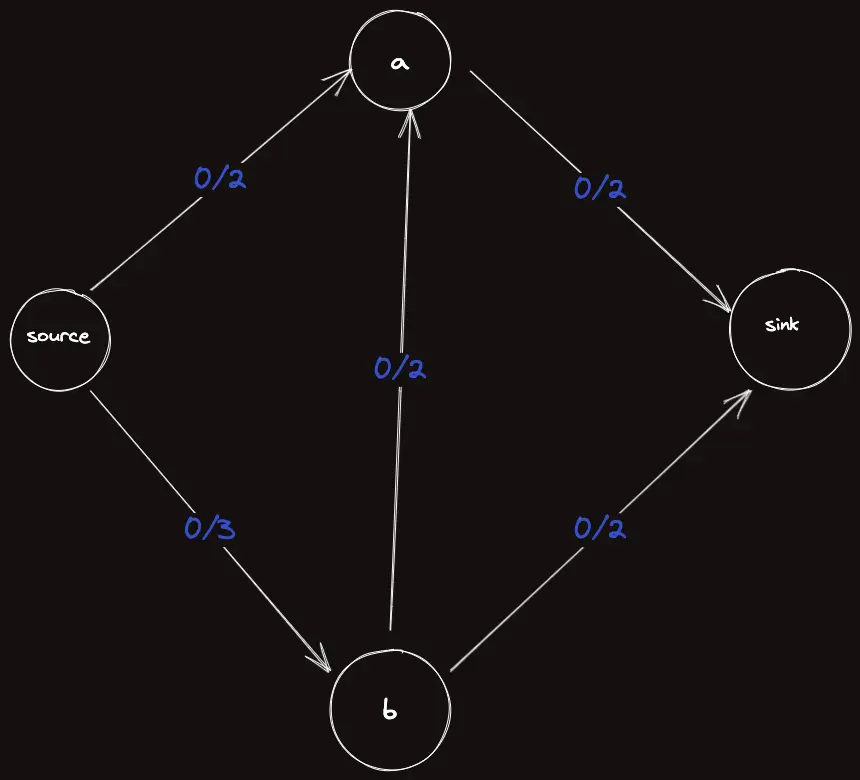
$source$ 에서 시작해서 $source \to b \to a \to sink$ 처럼 유량을 한 번 흘렸다고 하자.
이 경로에서 각 간선에서 (남은 용량-흐르고 있는 유량)중 최소는 $2$이므로 $2$만큼 흘릴 수 있다.
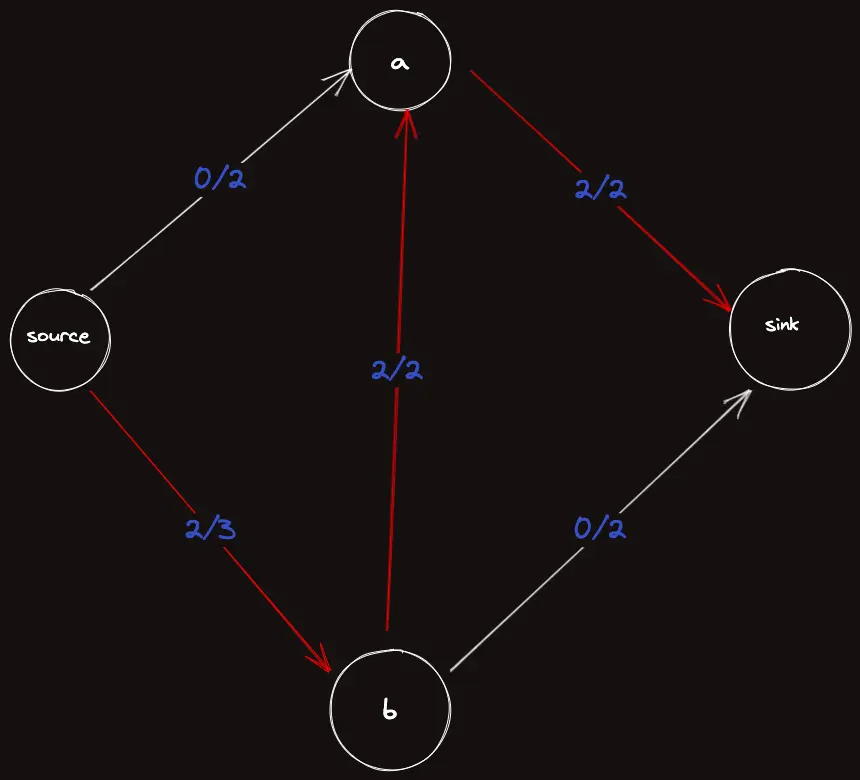
이제 $source$ 에서 다시 유량을 흘려보내자. $source \to b \to sink$ 로 진행되었다고 하자.
이 때는 흐를 수 있는 양의 최소값이 $1$이기 때문에 $1$만 흘려보낸다.
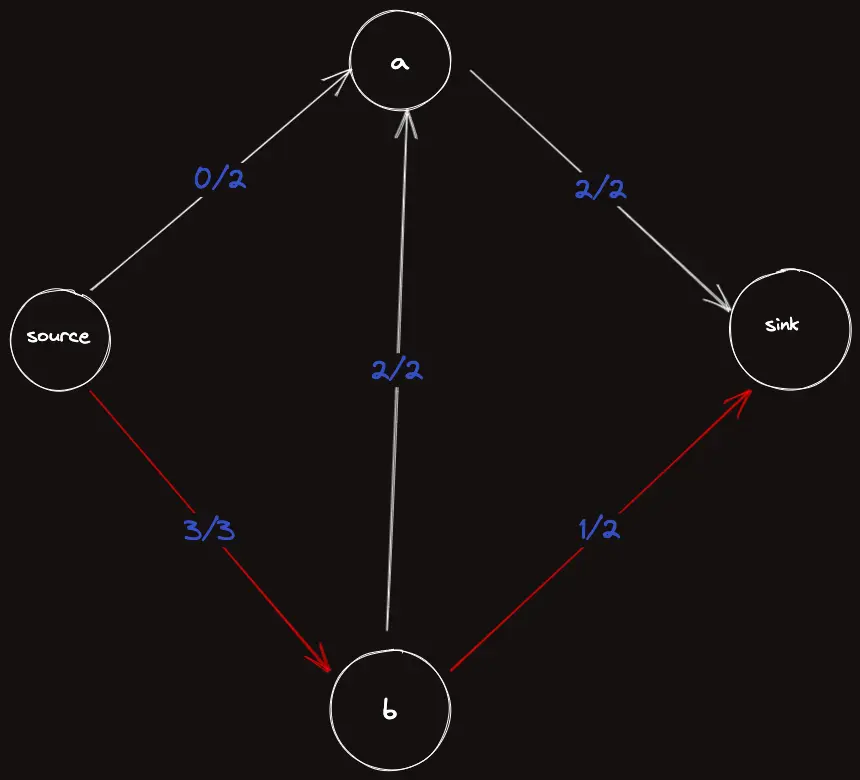
이제 $sink$ 에 $3$의 유량이 흐르고, $source \to a$로 가도 $a$에서 더 이상 흐를 수 있는 유량이 아무 간선도 안남아있기 때문에 알고리즘이 종료될 것이다.
하지만 우리가 그냥 대충 봐도 이 그래프에서 최대 유량은 $4$ 이다. 위로 $2$, 아래로 $2$ 를 흘려주면 되기 때문이다.
이를 해결하는 방법은 바로 성질 3이였던 어떤 간선엔 음의 유량만큼 흐르고 있다는 사실을 이용하는 것이다.
단방향 그래프에서 역방향 간선의 용량은 $0$ 이다.
하지만 무방향 그래프에선 역간선의 용량도 $c[u][v]=c[v][u]$ 로 설정해주어야 함에 유의한다. 이러한 개념을 제대로 잡고가지 않으면 무방향 그래프에서 어버버하다 풀 수 없다.
이를 그래프에 표시하면 다음과 같다.
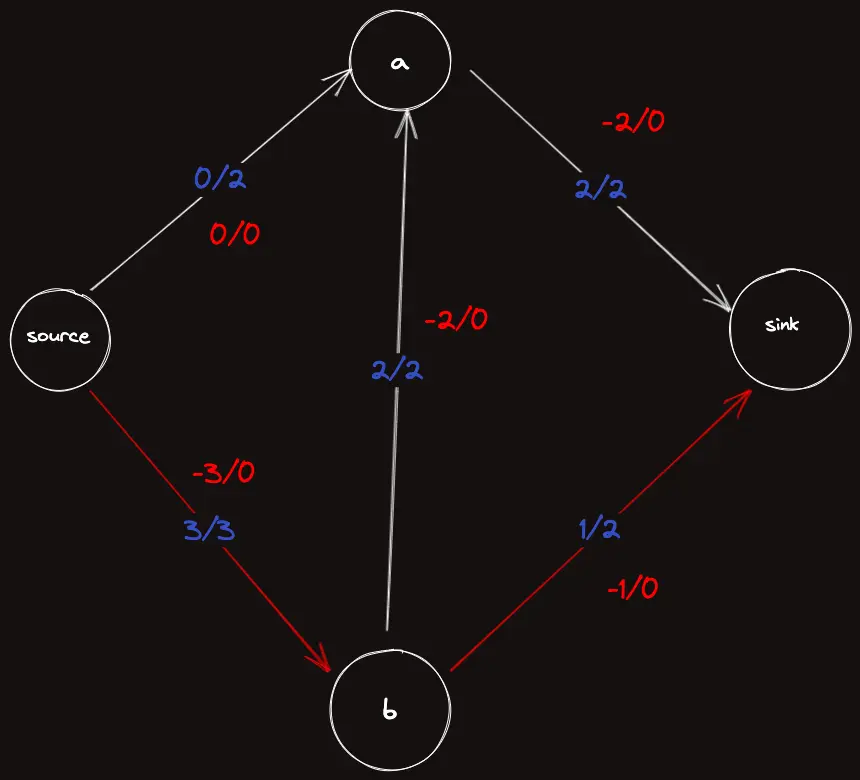
이제 음의 유량을 가진 간선을 $source \to a \to b \to sink$ 의 경로에 $1$의 유량을 흘려보낼 수 있다는 것이 보인다.
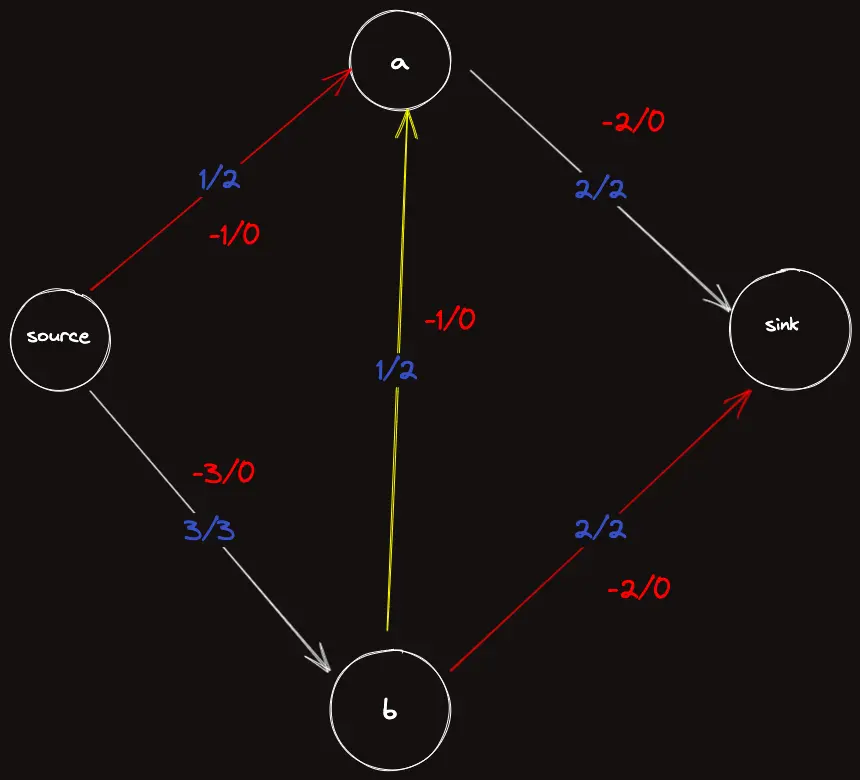
결과적으로 봤을 때는 실제로 $source \to a \to b \to sink$ 같은 경로를 거쳐 유량이 흐르는건 아니게되지만, 이런 방식으로 $source \to sink$ 로 흐르는 최대 유량을 찾아낼 수 있게 된 것이다.
포드-폴커슨 알고리즘은 정확히 이런 과정을 진행한다.
- $source \to sink$ 로 진행하며, (용량 - 유량)이 남아있는 간선들을 거쳐 $sink$ 에 도달한다. 이 경로를 증가 경로(augmenting path)라 한다.
- 거친 간선들 중 (용량 - 유량)의 최소값을 찾는다. 이 최소값을 가지는 간선을 차단 간선(blocking edge)이라고 한다.
- 경로상의 모든 간선에 $2$번에서 찾은 값만큼 유량을 더해주고, 해당 간선들의 역간선엔 빼준다.
- $sink$ 에 도달할 수 없을 때까지 반복한다.
증명
왜 증가 경로를 더 이상 찾을 수 없으면 그때까지 흘린 유량이 정답이 될까?
이는 이 글 에서 최소컷 정리를 설명하며 같이 증명된다.
시간 복잡도
매번 증가 경로를 찾는건 $DFS$든 $BFS$든 그래프 순회를 진행하기 때문에 $O(E)$가 걸린다.
이제 차단 간선이 가지는 값만큼 유량이 계속해서 추가되다가 $sink$에 도달하지 못하는 시점에 알고리즘이 종료되는데, 이 횟수는 몇번일까?
최악의 경우 이 값은 정답 유량에 정비례한다. 왜냐하면 계속해서 $1$만 흘릴 수 있는 아름다운 그래프가 존재한다면 말도안되는 시간복잡도가 나온다.
애초에 PS에서 용량과 유량의 절대적인 값은 제한을 잘 안걸기 때문에 포드-폴커슨으로 문제를 해결할 수 없는 경우가 대부분이다.
이를 개선한 것이 에드몬드-카프 알고리즘이다.
2. Edmonds-Karp
에드몬드 카프 알고리즘은 포드-폴커슨 알고리즘과 비슷하게 동작하지만, 좀더 시간복잡도가 개선된 알고리즘이라고 할 수 있다.
에드몬드 카프 알고리즘의 핵심은 매번 가장 짧은 증가 경로로 유량을 흘려보내는 것이다.
이렇게 되면 유량의 최단 경로의 길이가 계속해서 단조증가한다.
유량의 최단 경로의 길이가 단조증가함에 대한 증명
증가 경로를 찾기 전의 그래프를 $G$라 하고, 찾은 후의 그래프를 $G’$ 라 한다.
$G$의 용량이 남아있는 간선만 모아서 만든 집합을 $E$라 하고, $G’$의 간선의 집합을 $E’$ 라 한다.
$G’$ 가 있을 때, $sink$까지 최단 경로가 짧은 순으로 정점들을 정렬한다.
이 때, 각 그래프에서 정점 $u$의 $sink$ 까지의 최단 경로를 $d_G(u)$ 와 $d_{G’}(u)$ 라 한다.
보이려고 하는 것은 모든 정점 $u$에 대해 $d_{G’}(u) \ge d_G(u)$ 인 것이다.
귀납적으로 증명을 할 수 있다.
$d_G(sink)=d_{G’}(sink)=0$ 이므로 자명하다.
정점 $u$에서 $sink$까지 도달할 수 없는 경우, $d_{G’}(u)=\infty$ 라고두면 $\infty \ge d_G(u)$ 이므로 도달할 수 있는 간선들로만 살펴보는 범위를 좁혀보자.
어떤 정점 $u$에서 $sink$까지의 최단경로를 만들었을 때 $u$ 다음에 나오는 정점을 $v$ 라 하자.
$\overrightarrow {uv} \in E$ 라면, $d_{G’}(u)=d_{G’}(v)+1 \ge d_G(v)+1 \ge d_G(u)$ 이다.
첫 번째 부등식은 $G’$에서 $v$가 $u$보다 먼저 방문되었기 때문에 귀납가정에 의해 성립한다.
두 번째 부등식은 $\overrightarrow {uv} \in E$ 이기 때문에 $G$ 에서도 간선이 존재했으므로 성립한다.
그냥 $u$에서 $v$로 가서 $sink$로 가는 최단경로를 타면 되기 때문
$\overrightarrow {uv} \notin E$ 라면, 이번 증가 경로를 통해 유량을 흘리고 간선이 없었는데 $\overrightarrow {uv} \in E’$ 가 된 것이므로, 역간선을 이용해 증가 경로에 포함된 경우가 된다.
즉, $d_G(u)=d_G(v)+1$ 이고, $d_{G’}(u)=d_{G’}(v)+1 \ge d_G(v)+1 = d_G(u)$ 가 되어 증명된다. $\square$
시간복잡도 증명
에드몬드 카프 알고리즘의 시간 복잡도는 ${\color{salmon} O(VE^2) }$ 이다. 이걸 살펴보자.
단순 경로의 길이는 $V-1$ 개가 있다.
하나의 증가 경로를 찾았을 때 그 경로에 존재하는 하나 이상의 차단 간선은 용량이 꽉 찬다.
그 간선 $e$가 다시 차단 간선으로 동작하기 위해서는 그 간선에 역방향 유량이 흘러 다시 여유 용량이 생겨야 한다.
$G_1$ 이 현재 상태이고 $G_3$ 이 유량이 두 번 더 흐른 뒤의 상태라고 하자.
$d_{G_3}(u)=d_{G_3}(v)+1 \ge d_{G_2}(v)+1 = d_{G_2}(u)+2 \ge d_{G_1}(u)+2$ 위 식을 보면 유량을 더 흘려서 $\overrightarrow {uv}$ 를 바로 다시 차단 간선으로 만드려고 해도, $sink$ 까지의 거리가 최소 $2$가 늘어나기 때문에 하나의 고정된 증가경로의 길이 당, $O(E)$ 개에 수렴하는 경로밖에 나오지 않음을 알 수 있다.
즉, $O(E)$ 번이면 하나의 경로의 길이에 대해서 모든 유량을 흘려볼 수 있다는 것이다.
길이의 가지수가 $O(V)$ 이고 한 길이마다 $O(E)$ 번 흘리면 유량 알고리즘이 종료가 되고, 한 번 순회에 $O(E)$가 걸리므로 $O(VE^2)$ 이다.
구현
에드몬드 카프 알고리즘은 $10$번 정도 직접 구현해보면 눈감고도 구현할 수 있다.
하지만 구현법에 대해서는 이것저것 있을 수 있다.
인접 행렬을 이용하든, 인접 리스트를 이용하든 문제의 상황에 맞게 적절히 구현해주면 된다.
이 문제를 풀어보자.
인접 리스트를 이용해 풀었다.
int N, K, D, s, e;
vi A, B;
vi edges[302];
int C[302][302], F[302][302];
int flow() {
int ret = 0;
while (1) {
queue<int> q;
vi prev(N + D + 2, -1);
q.push(s);
while (sz(q)) {
int cur = q.front();
q.pop();
for (int to: edges[cur]) {
if (C[cur][to] - F[cur][to] > 0 && prev[to] == -1) {
prev[to] = cur;
q.push(to);
}
}
}
if (prev[e] == -1) break;
int f = 1e9;
for (int c = e; c != s; c = prev[c]) f = min(f, C[prev[c]][c] - F[prev[c]][c]);
for (int c = e; c != s; c = prev[c]) {
F[prev[c]][c] += f;
F[c][prev[c]] -= f;
}
ret += f;
}
return ret;
}
void solve() {
cin >> N >> K >> D;
s = N + D, e = s + 1;
// source -> 사람들
for (int i = 0; i < N; i++) {
C[s][i] = K;
edges[s].pb(i);
}
// 음식 -> sink
for (int i = 0, c; i < D; i++) {
cin >> c;
C[i + N][e] = c;
edges[i + N].pb(e);
}
// 사람들 -> 음식
for (int i = 0; i < N; i++) {
int Z;
cin >> Z;
for (int j = 0, d; j < Z; j++) {
cin >> d, d--;
C[i][d + N] = 1;
edges[i].pb(d + N);
edges[d + N].pb(i);
}
}
cout << flow();
}
가중치가 모두 1이기 때문에 $dist$ 같은 배열을 관리하지 않아도 상관없이 방문한 정점을 다시 안방문 하는것만으로 $sink$ 까지의 최단경로를 구할 수 있다.
템플릿
필자가 이전에 만들어둔 Edmonds-Karp 알고리즘의 템플릿은 다음과 같다.
테크닉 & 흔한 문제들
kks227 님 글을 보고 유량을 처음 공부했기 때문에 여기에 있는 연습문제와 관련된 내용들이 많다.
무방향 간선의 유량
앞서 언급했듯이 무방향 간선의 유량은 역간선에도 동일한 만큼의 유량을 추가해줄 수 있다.
정점 분할 테크닉
사실 BOJ 2316 - 도시 왕복하기2 문제는 조금 특이해서 무방향 간선의 유량을 이용해도 바로 풀 수는 없다.
문제는 특이하게 각 도시를 한 번만 방문해야 된다는 조건이 있다.
이 때, 각 정점을 두 개의 정점으로 분할해주고 유량이 들어오는 정점과 유량이 나가는 간선으로 분리해줄 수 있다.
그런다음 두 간선 사이를 용량 1의 간선으로 이어주면 된다.
정점 $u$를 들어오는 정점 $in[u]$와 나가는 정점 $out[u]$ 로 분리해주자.
$\overrightarrow {uv}$ 였던 간선은 $\overrightarrow {out[u]in[v]}$ 가 된다.
게다가 이 문제는 무방향 그래프라 더 헷갈리는데, $\overline{uv}$ 였던 무방향 간선은
- $\overrightarrow {out[u]in[v]}$ 에 용량과 인접리스트에 간선을 추가하고
- $\overrightarrow {out[v]in[u]}$에 용량과 인접리스트에 간선을 추가하고
- $\overrightarrow {in[v]out[u]}$ 에 인접리스트에 간선을 추가하고 (역간선을 위해)
- $\overrightarrow {in[u]out[v]}$ 에 인접리스트에 간선을 추가한다.
그리고 각 정점마다
- $\overrightarrow {in[u]out[u]}$ 에 용량 1을 추가하고 인접리스트에 간선을 추가한다.
$out[u] \to in[u]$ 로의 인접리스트 간선은 추가하지 않아도 문제가 통과 되는데, 증가 경로가 역방향 유량이 흐르기 때문에 $out[u] \to in[u]$ 로 흐른다 해도, 어차피 $in[u] \to out[u]$ 로 들어왔을 것이기 때문에 $sink \to source$ 로 역추적 하는 과정에서 적절히 적용이 될 것이기 때문이다.
다음은 소스 코드이다.
고급 - 유량 되돌리기
이 문제는 유량을 흘려보고 사전순으로 가장 빠르게 하기 위해 흘린 유량을 다시 롤백했다가 다시 다른쪽으로 흘려보고 해야하는 문제이다.
$A, B$ 팀의 합이 다르거나 최대 유량이 인원수대로 안나오면 일단 정답은 $-1$ 이다.
이 문제는 이분 그래프처럼 생긴 그래프가 주어지는 문제라서 유량을 롤백하는 것을 복잡하게 구현안하고 세 개의 간선에 대해서만 유량을 롤백했다가, 현재 간선을 안쓰고 다시 흘려봐서 가능하면 교체해주는 방식으로 구현이 가능하다.
사전순으로 앞선 자리부터 $y \to x$ 를 용량을 0으로 설정해가며 막아가면서 $3$개의 간선의 유량을 롤백하고 다시 흘려보고 만약 흘릴 수없다면 기존으로 바꿔주는 식으로 사전순으로 가장 빠른 대진표를 찾을 수 있다.
const int MAX = 105;
int N, M;
vi A, B;
vi edges[MAX];
int C[MAX][MAX], F[MAX][MAX];
int flow(int s, int e) {
int ret = 0;
while (1) {
vi prev(MAX, -1);
queue<int> q;
q.push(s);
while (sz(q)) {
int cur = q.front();
q.pop();
for (int to: edges[cur]) {
if (prev[to] == -1 && C[cur][to] - F[cur][to] > 0) {
prev[to] = cur;
q.push(to);
}
}
}
if (prev[e] == -1) break;
int mf = 2e9;
for (int i = e; i != s; i = prev[i])
mf = min(mf, C[prev[i]][i] - F[prev[i]][i]);
for (int i = e; i != s; i = prev[i])
F[prev[i]][i] += mf, F[i][prev[i]] -= mf;
ret += mf;
}
return ret;
}
int in(int i) { return i * 2; }
int out(int i) { return i * 2 + 1; }
void solve() {
cin >> N >> M;
A.resize(N), B.resize(M);
fv(A);
fv(B);
if (acc(A) != acc(B)) {
cout << -1;
return;
}
int s = N + M, e = s + 1;
for (int i = 0; i < N; i++) {
C[s][i] = A[i];
edges[s].pb(i);
}
for (int i = 0; i < M; i++) {
C[i + N][e] = B[i];
edges[i + N].pb(e);
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
C[i][j + N] = 1;
edges[i].pb(j + N);
edges[j + N].pb(i);
}
}
int mf = flow(s, e);
if (mf != acc(A)) {
cout << -1;
return;
}
for (int y = 0; y < N; y++) {
for (int x = N; x < M + N; x++) {
C[y][x] = 0;
if (F[y][x]) {
F[s][y]--, F[y][s]++;
F[y][x]--, F[x][y]++;
F[x][e]--, F[e][x]++;
if (!flow(s, e)) {
F[s][y]++, F[y][s]--;
F[y][x]++, F[x][y]--;
F[x][e]++, F[e][x]--;
}
}
cout << F[y][x];
}
cout << endl;
}
}
고급 - 2차원 격자와 관련된 문제들
두부장수 홍준…류의 문제들이나 BOJ 11495 - 격자 0 만들기 같은 문제들을 최대 유량 그래프로 모델링해서 풀 수 있는 경우가 많다.
하지만 이건 좀더 이분 그래프와 이분 매칭쪽 개념을 알고나서 풀어야 이것 저것 문제도 풀고 이해도 더 잘 할 수 있기 때문에 이 글에서 다루진 않으려 한다.
Where to next?
다음과 같은 포스트들이 써질 예정이다.
- Min Cut - Maximum Flow 정리
- Bipartite Graph와 Bipartite Matching에 대한 내용들
- Maximum Bipartite Matching
- Minimum Vertex Cover
- 등
Comments