Convex Hull Trick DP
Convex Hull Trick
Convex Hull Trick, 줄여서 CHT는 DP 최적화 기법 중 하나이다.
점화식
우리가 DP문제를 풀려는데 위처럼 식이 구성된다고 해보자.
이는 $i,j \le N$ 이기 때문에 보통 $O(N^2)$ 이 걸린다.
그런데 $N=100,000$ 같은 문제는 해결할 수 없는 것일까?
아니다. CHT를 쓰면 가능하다.
제한
CHT는 점화식만 정해진 꼴로 나오면 입력에 대한 제한이 없다.
데이터의 제한에 따라 좀 더 간편하고 빠른 구현법이 존재할 수는 있지만, 제한이 없다고 해도 조금 복잡한 친구들을 이용해 PS에서 통용되는 시간복잡도 안에 풀 수 있는 문제가 대부분이다.
아이디어
$dp[i]=Max_{0 \le j < i}\left( M[j]X[i]+K[j]+C[i] \right)$
를 잘 보면, $C[i]$ 는 어차피 $i$ 랑만 연관되어 있는 값이므로 $j$ 랑 상관없으므로 식에서 고려해줄 필요가 없다.
따라서 관심있는 ${\color{salmon} M[j]X[i]+K[j] }$ 만 살펴보면 되는데, 이 꼴은 바로 일차함수와 같다!
그러므로 $j$에 대해서 $M[j]$ 를 기울기로 갖고 $K[j]$ 를 $y$ 절편으로 갖는 직선들을 관리해줌으로 $M[j]X[i]+K[j]$ 의 최대(최소)값을 빠르게 구해줄 수 있을 것 같다.
$j$란건 지금까지 거쳐온 $i$ 값들 중 하나이므로 현재 $i$ 를 처리해줬으면 $M[i]$와 $K[i]$ 라는 값으로 직선을 추가해줄 수 있다.
$M[j], X[i], K[j], C[i]$ 란 값들은 모두 배열을 의미하는 것이 아니다. 이 값들을 얻어오는 함수일 수 있고 알고리즘일 수 있다. 이러한 것들은 얻어오는데 걸리는 시간복잡도 만큼 전체 시간복잡도에 영향을 미친다.
이제 정말 저 직선들을 기하학적으로 그려보면서 어떻게 CHT가 이 직선들을 이용해 빠르게 최대/최소 값을 찾을 수 있는지 알아보자.
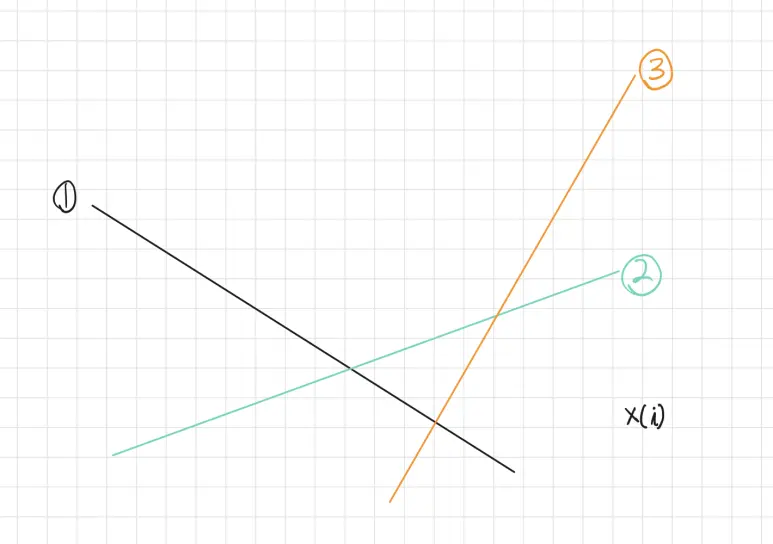
이렇게 평면에 직선들이 있다. 가로축은 $X[i]$ 를 의미하므로, 어떤 $i$에 대해 $x=X[i]$ 를 대입해서 어떤 직선과의 접점의 $y$좌표가 제일 크거나(최댓값을 찾을 때), 제일 작거나(최솟값을 찾을 때)를 따져주면 된다.
일반성을 잃지않고 최대값을 찾는다고 하자.
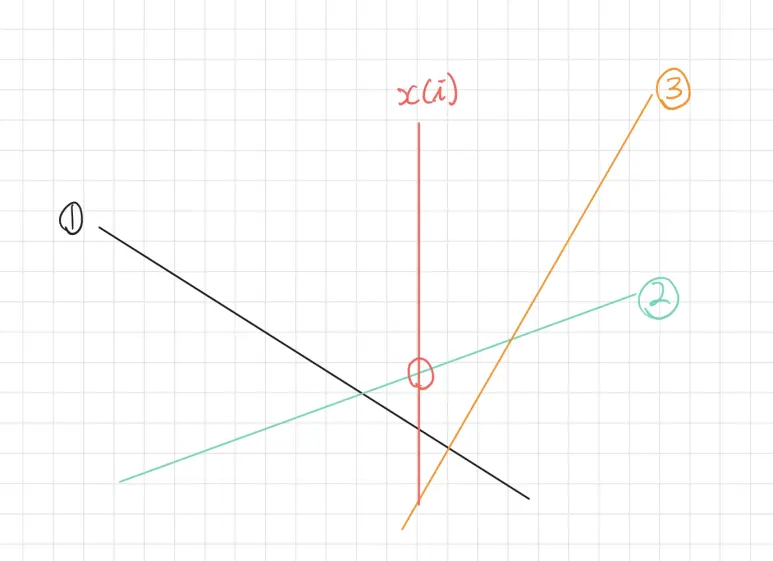
이걸 보면 $2$번 직선과 $X[i]$ 와의 교점이 가장 $y$ 가 크기 때문에 $j=2$ 일 때 최대값이 되어서 저 $2$번 직선과의 $M[j]X[i]+K[j]+C[i]$ 가 $dp[i]$ 이 될 것이다.
직선 관리
그럼 어떤 직선과의 교점이 가장 최댓값인지는 어떻게 알 수 있을까?
직선들은 $M[j]$ 기울기로 정렬되어 관리하자.
각 직선마다 인접한 바로 다음 직선과의 교점들의 $x$ 좌표가 있다고 할 때, 이 좌표들을 같이 관리하며 이분 탐색으로 찾아야 할 직선을 $O(\log N)$에 찾는 것이다.
문제의 제한에 따라 최적화가 가능해서 특별한 경우, $O(1)$ 에도 찾을 수 있다. 관련된 특이사항들은 후술한다.
구현에 따라 바로 전 직선과의 교점을 저장해둬도 되고, 가장 끝 직선들의 교점 좌표는 $\infty$(바로 다음 직선과의 교점인 경우)나 $-\infty$(직전 직선과의 교점인 경우)로 관리된다.
그런데 의아한 점은 기울기로 정렬이 되어 있어도 다음 교점과의 좌표는 정렬되어있지 않을 수 있다는 점이다.
모든 직선을 넣으면 될까?
이런 경우를 보자.
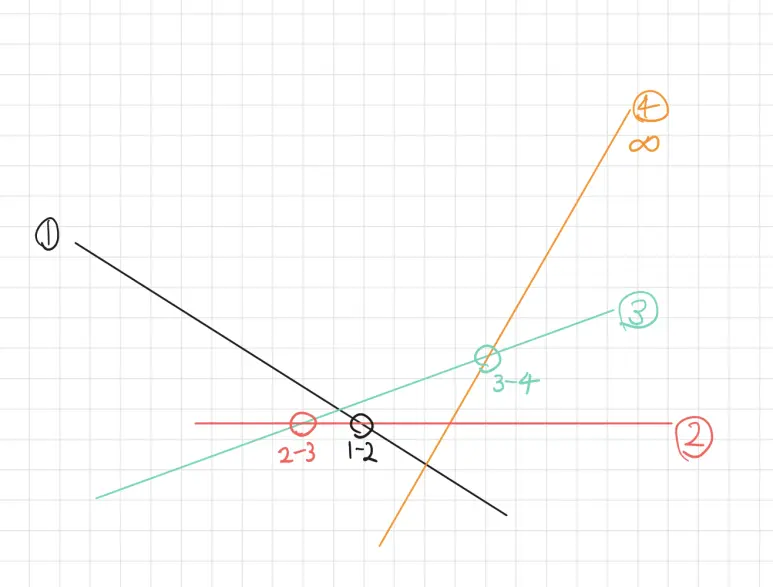
기울기는 $1,2,3,4$ 순으로 정렬이 되어서 번호가 붙어있지만, 그 다음 인접한 기울기를 가진 직선과의 교점은 그렇지 않다.
$2-3$ 직선 교점은 $1-2$ 직선의 교점보다 뒤에있다.
우리가 $2-3$ 교점보다 작은 $X[i]$ 를 갖고 이분탐색을 돌리면 실제 정답은 $1$ 번 직선과의 교점의 $y$값이 최댓값인데 $2-3$ 교점이 탐색되어서 $2$ 번 교점과의 교점의 $y$ 좌표로 잘못된 값을 얻게된다.
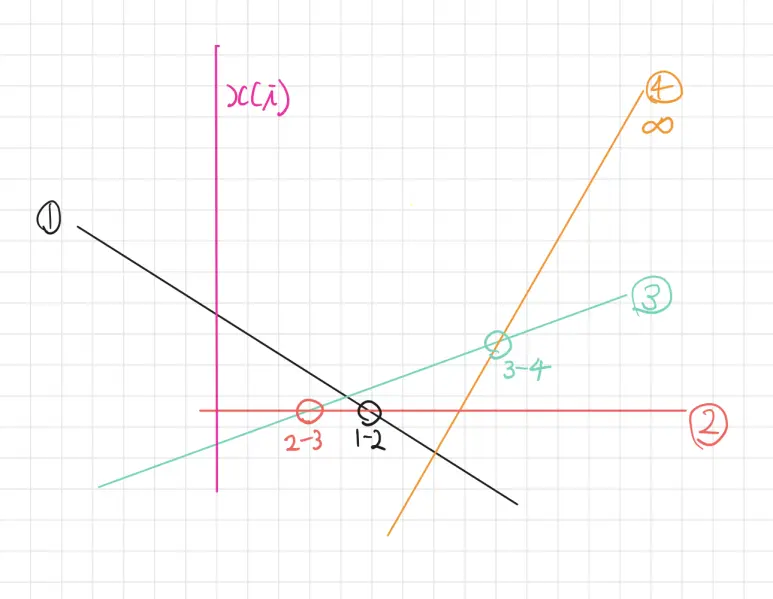
이를 방지하려면 어떻게 해야할까?
우리가 관심있는 부분은 저 직선들의 집합에서 어떤 부분일지 생각해보자.
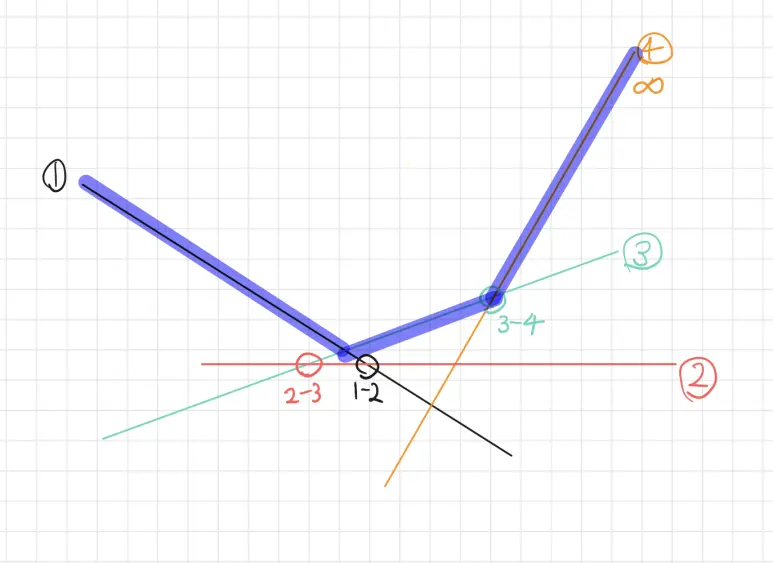
바로 이렇게 볼록하게 생긴 부분이다. 따라서 이 부분에 기여를 못하는 $2$ 번 직선 같은 친구들은 방해만 되고 삭제해줌이 맞다.
이 모양새 때문에 바로 Convex Hull Trick이라 불린다.
$i$ 번 째 직선과 $j$ 번 째 직선의 교점을 $x[i][j]$ 라 할 때, $x[i-1][i] > x[i][i+1]$ 이라면 $i$ 번 째 직선은 삭제되어야 한다.
위의 예시에선 $1-2$ 교점 좌표가 $2-3$ 교점 좌표보다 크기 때문에 $2$ 번 직선이 삭제되어야 한다.
- $i$ 번 째 직선이 $x>x[i][i+1]$ 인 구간에서 어떤 $X[i]$ 와 교차해 최댓값이 될 수 없다.
- $i+1$ 번 째 직선이 $i$ 번 째 직선보다 기울기가 크기 때문이다.
- $i$ 번째 직선이 $x<x[i-1][i]$ 인 구간에서 어떤 $X[i]$ 와 교차해 최댓값이 될 수 없다.
- $i-1$ 번 째 직선이 $i$ 번 째 직선보다 기울기가 작기 때문이다.
따라서 $i$ 번 째 직선이 사용될 수 있는 구간은 $x[i-1][i] \le x \le x[i][i+1]$ 인데, 이 구간에서 조차 쓸모가 없다면 삭제되어야 함이 맞다.
최적화 기법
원리를 살펴보았으니 구현에 앞서 몇가지 짚고 넘어가야할 점들이 있다.
$M[j]$ 가 무작위일 때
기울기가 무작위라는 것은 우리가 기울기를 정렬 기준으로 직선들을 관리함에 있어 직선들 사이에 다른 직선을 끼워넣어줄 수도 있다는 뜻이다.
이것의 구현은 $M[j]$가 단조증가할 때보다 복잡하고 보통 LineContainer 라는 멀티셋 구현체나 리차오 트리라는 자료구조를 이용해 구현된다.
이는 직접짜는 것보다 템플릿을 활용하는 것이 심신의 안정을 얻을 수 있다.
직선을 추가하는데는 $O(\log N)$ 이 걸리고, 쿼리도 $O(\log N)$이 걸리게 된다.
$M[j]$ 가 단조성이 있는 경우
직선 추가에 있어 스택을 활용해서 $O(1)$에 할 수 있다.
모든 직선을 다루므로 결국 전체 과정에서는 $O(N)$ 이다.
기울기가 단조성이 있는 상태로 들어오므로 조건에 맞는 시점까지 pop 해준다음 자신을 삽입하면 되기 때문이다.
교차점의 $x$ 좌표를 확인하는 과정은 $O(1)$ 이기 때문이다.
$X[i]$ 에 단조성이 있는 경우
$M[j]$ 가 $O(1)$ 로 순회할 수 있도록 설계되어 있는 경우, $X[i]$ 에 단조성이 있으면 쿼리도 $O(1)$ 에 가능하다.
물론 전체 과정에서는 $O(N)$ 이다.
직선들에 대한 포인터를 유지시키며 현재 보고 있는 직선의 다음 직선과의 교차점이 $X[i]$ 보다 작다면 다음 직선으로 넘어가도록 구현해주면 된다.
교차점을 정수로 다루기
직선들의 교차점의 $x$ 좌표가 실수로 나와도 정수로 다루어줄 수 있다.
단, $X[i]$ 가 정수일 때만이다.
왜냐면 실수 좌표에 쿼리가 들어오지 않으면 교차점의 $x$ 좌표도 실수로 다루어 줄 필요가 없기 때문이다.
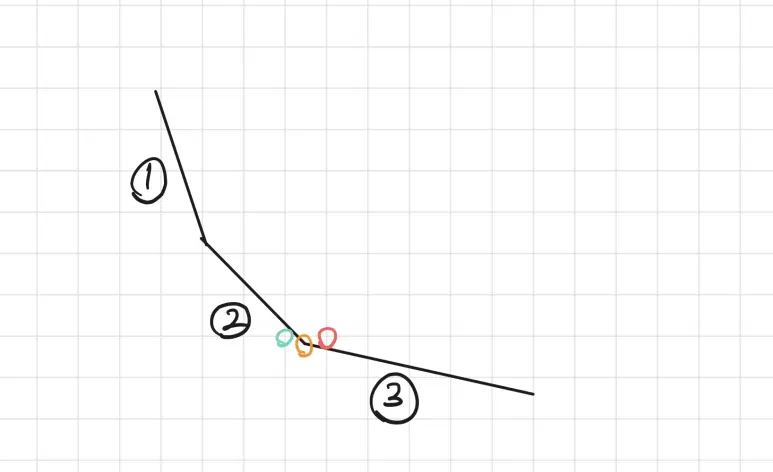
격자를 정수 좌표라고 하고, $x[2][3]$인 주황색 점은 실수 좌표가 되지만 그냥 초록색 점으로 교차점의 $x$ 좌표를 저장해주어도 된다.
초록색에 쿼리가 들어오면 원래 $2$ 번 직선과 만나야 했는데, 문제 없이 잘 만나게 되고,
빨간색에 쿼리가 들어오면 $3$ 번 직선이 찾아져야 했으므로 옳다.
c++ 구현상에서 나눗셈 연산을 했을 때 $x$ 좌표가 음수라면 $-1$ 을 한 번 더 해줘야 한다.
구현
문제에 따라 구현법은 상이할 수 있으므로 일전에 언급한 LineContainer 의 구현체를 첨부한다.
struct line {
mutable ll m, k, p;
bool operator<(const line &o) const { return m < o.m; }
bool operator<(ll x) const { return p < x; }
};
struct CHT : multiset<line, less<>> {
//(for doubles, use inf = 1/.0, div(a,b) = a/b)
const static ll inf = LLONG_MAX;
ll div(ll a, ll b) { return a / b - ((a ^ b) < 0 && a % b); }
bool isect(iterator x, iterator y) {
if (y == end()) return x->p = inf, 0;
if (x->m == y->m) x->p = x->k > y->k ? inf : -inf;
else x->p = div(y->k - x->k, x->m - y->m);
return x->p >= y->p;
}
void add(ll m, ll k) { //add y = mx + k
auto z = insert({m, k}), y = z++, x = y;
while (isect(y, z)) z = erase(z);
if (x != begin() && isect(--x, y)) isect(x, y = erase(y));
while ((y = x) != begin() && (--x)->p >= y->p) isect(x, erase(y));
}
ll query(ll x) {
auto l = *lower_bound(x);
return l.m * x + l.k;
}
} cht;
이걸 가지고 문제를 풀어보자.
연습 문제
BOJ 13263 - 나무 자르기
정말 대표적인 연습문제이다.
이 문제는 $M[j]$ 와 $X[i]$ 에 모두 단조성이 있으므로 $O(N)$에 해결이 가능하다.
일단 위 구현체를 써서 쉽게 푼 후에 그렇게도 풀어보자.
$dp[i]=i$ 번째 나무가 높이가 $1$ 남아있고 전기톱이 충전되어 있을 때 지금까지 쓴 충전 비용의 최솟값이라고 하자.
$a[1]=1$이므로 $dp[1]=0$ 이고 정답은 $dp[N]$ 이다. $N$ 번 째 나무를 베면 모든 나무를 비용없이 벨 수 있기 때문이다.
그러면 식을 다음과 같이 세울 수 있다.
즉, $M[j]=b[j]$ 이고 $X[i]=a[i]$ 이고, $K[j]=dp[j]$ 이다.
그런데 이 문제는 최댓값을 구하는 문제가 아니고 최솟값을 구하는 문제이므로 CHT 구현체가 최댓값을 구하도록 구현되어 있다면 적절히 음수로 변환을 해서 풀어야 한다.
음수로 변환을 해주어야 할 값들은 직선과 관련된 값들 $M[j], K[j]$ 이다.
따라서 CHT 를 이용해 풀 수 있다.
void solve() {
int n;
cin >> n;
vector<ll> a(n + 1), b(n + 1), dp(n + 1);
fv1(a);
fv1(b);
cht.add(-b[1], -dp[1]);
for (int i = 2; i <= n; i++) {
dp[i] = -cht.query(a[i]);
cht.add(-b[i], -dp[i]);
}
cout << dp[n];
}
이제 최적화를 적용해서 직접 직선들을 관리하는 구현도 포함해서 코드를 짜보자.
위 구현은 업데이트에 $O(\log N)$, 쿼리에 $O(\log N)$이 걸린다.
struct line {
mutable ll m, k, x;
double cross(const line &o) {
// m1x + k1 = m2x + k2
// (m1-m2)x = k2-k1
// x = (k2-k1)/(m1-m2)
return 1.0 * (o.k - k) / (m - o.m);
}
};
void solve() {
int n;
cin >> n;
vector<ll> a(n + 1), b(n + 1), dp(n + 1);
fv1(a);
fv1(b);
vector<line> lines;
int p = 0;
for (int i = 2; i <= n; i++) {
while (p < sz(lines) - 1 && lines[p + 1].x <= a[i]) p++;
dp[i] = a[i] * lines[p].m + lines[p].k;
line new_line = {b[i], dp[i]};
while (sz(lines)) {
if ((new_line.x = new_line.cross(lines.back())) <= lines.back().x) lines.pop_back();
else break;
}
lines.pb(new_line);
}
cout << dp[n];
}
위 코드는 line 의 x 가 직전 직선과의 교점을 저장하게 구현한 코드이다.
최솟값 CHT를 구하게 구현을 하려면 다음 직선과의 교점이 아닌 직전 직선과의 교점을 다루면 된다.
총 $O(N)$ 이 걸린다.



Comments