Clustering 알고리즘들

이 글은 8 Clustering Algorithms in Machine Learning that All Data Scientists Should Know를 공부하고 적힌 글입니다.
Unsupervised Learning(비지도 학습은) 데이터셋에 완전히 정답 Label이 없는 데이터를 가지고 수행하는 머신러닝이며 우린 심지어 어떤 숨겨진 패턴이 데이터에 존재하는지도 알 수 없다. 알고리즘이 이것을 찾도록 만들어야한다.
이럴때 Clustering Algorithm을 쓸 수 있다.
Clustering AlgorithmsPermalink
Clustering은 unsupervised machine learning task이며 label이 없는 많은 데이터를 가지고 그룹화를 하는 과정이다.
이 그룹들은 clusters라고 불리며 clusters는 그것들의 근처의 data points들에 대한 상관을 기반으로 비슷한것들끼리 묶인 그룹이다.
Types of clustering algorithmsPermalink
많은 종류의 특징있는 데이터들을 clustering할 수 있는 알고리즘들이 있다.
Density-based (밀도기반군집)Permalink
Density-based clustering은 높은 집중도를 가진 데이터 점들이 낮은 집중도를 가진 데이터 점들로 둘러쌓인 형태를 의미한다.
알고리즘은 밀도가 높은 지점을 찾으며 그것을 cluster로 만든다.
유용한 점은 clusters들이 어떤 모양이든 가능하다는 것이다. 어떤 제한된 조건이 필요하지 않다.
이러한 종류의 clustering algorithms들은 이상치들을 clusters안에 포함시키지 않으며 그것들을 무시한다.
DBSCAN, Mean-shift, OPTICS과 같은 알고리즘이 여기에 속한다.
Distribution-basedPermalink
모든 데이터 포인트들이 cluster의 부분인지 그 cluster에 속할 확률을 기반으로 고려된다.
특정 center point가 있고 어떤 data point가 그 point에 밀접할수록 확률이 올라가는 방식으로 예시를 들 수 있겠다.
당신이 당신의 data가 어떤 distribution을 가져야할지 확신할 수 없다면 다른 알고리즘을 쓰는게 좋다.
Gaussian mixture방식이 여기에 속한다.
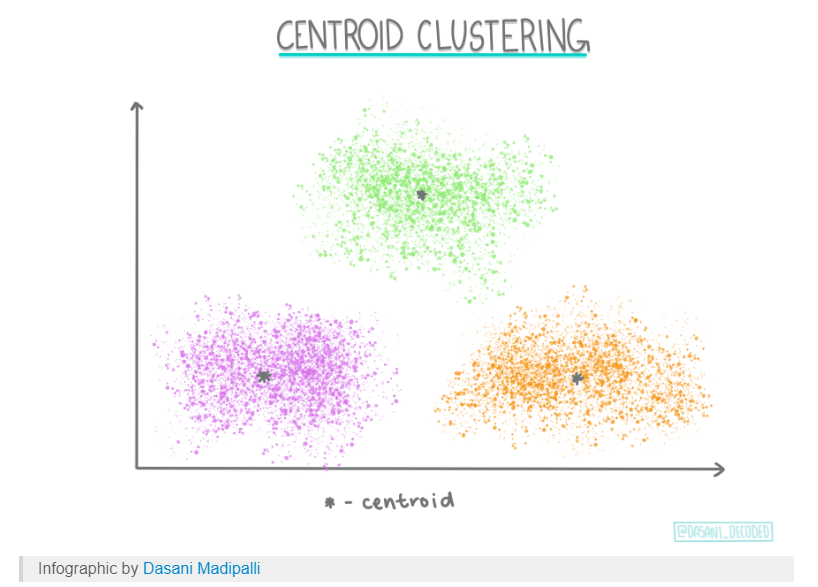
Centroid-basedPermalink
Centroid-based clustering은 아마 당신이 가장 많이 들어봤을 clustering이며 처음에 당신이 설정하는 hyper parameter에 민감한 알고리즘이다. 그리고 빠르고 효율적이다.
이 알고리즘은 data points를 여러개의 centroids로 분리한다.
각 data points들은 centroids들에게 squared distance기반으로 가까운 순으로 clustering되며 가장 흔하게 쓰이는 clustering 방법이다.
K-means 알고리즘이 여기에 속한다.
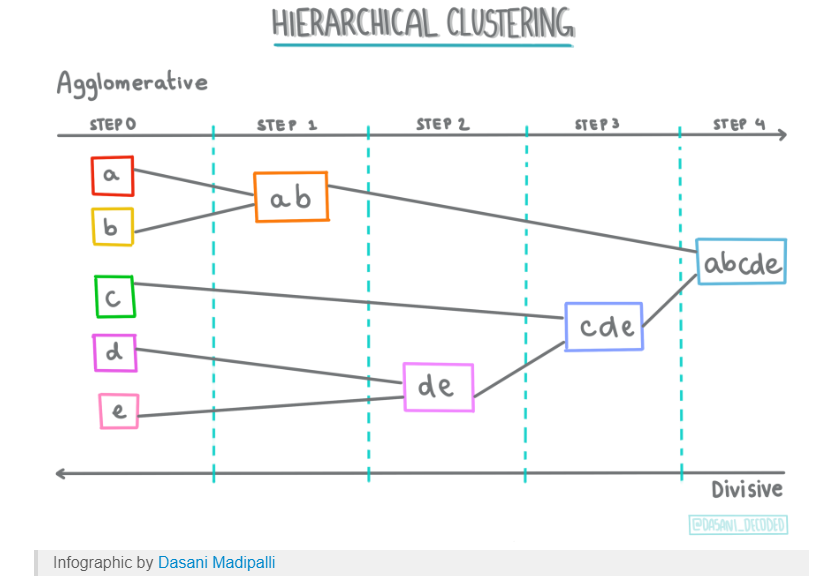
Hierarchical-basedPermalink
Hierarchical-based clustering은 계층적 데이터에 전형적으로 사용되며 Clusters의 Tree를 구성하며 top-down으로 구성되어나간다.
다른 Clustering types에 비해 제한적이지만 특정한 계층을 가지고있는 데이터셋에선 가장 최적이다.
Agglomerative Clustering, BIRCH들이 여기에 속한다.
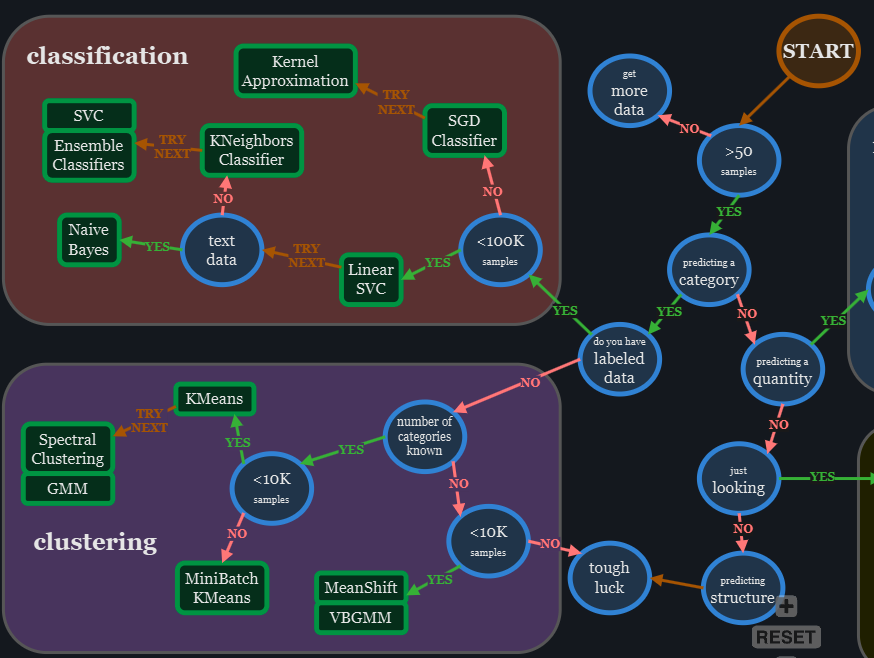
어떤 알고리즘을 골라야 하는가?Permalink
1. Connectivity-based (계층적 클러스터링)Permalink
- 개념: 거리 기반으로 데이터를 계층적으로 묶음
- 종류: Agglomerative(병합), Divisive(분할)
- 특징:
- 덴드로그램 생성
- 계층 구조 파악에 유용
- 단점:
- 속도 느림
- 비계층적 데이터에 부적합
- 정확한 클러스터 경계 제공 어려움
2. Centroid-based (K-means)Permalink
- 개념: 중심점(centroid)을 기준으로 클러스터 할당
- 특징:
- 계산 빠르고 구현 간단
- 중심 기준으로 군집화
- 단점:
- 클러스터 수(k)를 미리 지정해야 함
- 경계가 애매함
- 중첩된 데이터에는 부적합
3. Distribution (GMM)Permalink
- 개념: 각 데이터 포인트가 클러스터에 속할 확률을 기반으로 분류
- 도구: Gaussian Mixture Model (GMM)
- 특징:
- 중첩 가능
- 타원형 경계 표현
- 확률 기반으로 유연한 분류 가능
- 단점:
- 가우시안 분포 전제
- 실제 측정 데이터에 부적합할 수 있음
4. Density-based (DBSCAN)Permalink
- 개념: 밀도 기준으로 ε 이내 이웃 수를 바탕으로 클러스터 형성
- 특징:
- 클러스터 수 지정 불필요
- 임의 형태의 클러스터 탐지 가능
- 이상치 분리 가능
- 단점:
- 밀도 차이가 큰 경우 부적합
- ε 파라미터 설정이 어려움
✅ 알고리즘 선택 팁Permalink
| 조건 | 추천 알고리즘 | | ——————— | ———— | | 계층 구조가 있는 데이터 | Hierarchical | | 중심이 명확한 군집 | K-means | | 중첩된 클러스터 | GMM | | 복잡한 모양의 클러스터 + 이상치 처리 | DBSCAN | | | |
| 조건 | 추천 알고리즘 |
|---|---|
| 계층 구조가 있는 데이터 | Hierarchical |
| 중심이 명확한 군집 |
언제 Clustering을 써야하는가?Permalink
unlabeled data set을 가지고있을 때 사용한다.
unsupervised learning의 기법엔 Neural Network, Reinforcement Learning(강화학습) 그리고 Clustering이 있다.
당신의 데이터가 어떠한 형태인지에 따라 뭘 써야할지 다르다.
아마 이상치를 검출하기위해 Anomaly Detection을 수행하고 싶을때 이런 clusters grouping은 도움이된다.
또한 ML을 수행하기 전에 데이터의 features들에 대해서 잘 모르겠을 때 pattern을 검출하는데도 도움이된다.
Clustering은 아무것도 모르는 Data에 대해서 insight를 얻을 때 특히 유용하며 어떤 타입의 Clustering 기법을 사용할지 결정하는데 시간이 좀 걸릴 수 있지만 귀중한 insight를 얻을 수 있다.
Real world에서는 보험 사기 감지나 도서관의 책들을 분류하거나 마케팅에서 유저군을 분류하는데도 사용된다.
The Top 8 Clustering AlgorithmsPermalink
Scikit learn 라이브러리는 이 구현체들을 가지고있다.
_makeclassification data set 함수를 이용해 어떤 Clustering Algorithms이 모든 clustering 문제들에 잘 맞지않음을 보일것이다.
K-means clustering algorithmPermalink
K-means는 clustering 에서 가장 흔히 사용되는 알고리즘이다. Centroid Based의 알고리즘이며 가장 단순하다.
K-means는 작은 data set에 적합하다. 모든 data point에 대해 반복하기 때문에 큰 data set에선 성능이 나오지 않는다.
from sklearn.datasets import make_classification
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# 데이터 생성
X, y_true = make_classification(
n_samples=300, n_features=2, n_informative=2, n_redundant=0,
n_clusters_per_class=1, n_classes=3, random_state=42
)
print(X)
# KMeans 클러스터링
kmeans = KMeans(n_clusters=3, random_state=42)
y_pred = kmeans.fit_predict(X)
# 시각화
plt.figure(figsize=(6, 5))
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='viridis', edgecolor='k')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
c='red', s=100, marker='X', label='Centroids')
plt.title("KMeans Clustering (from make_classification)")
plt.legend()
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.grid(True)
plt.tight_layout()
plt.show()
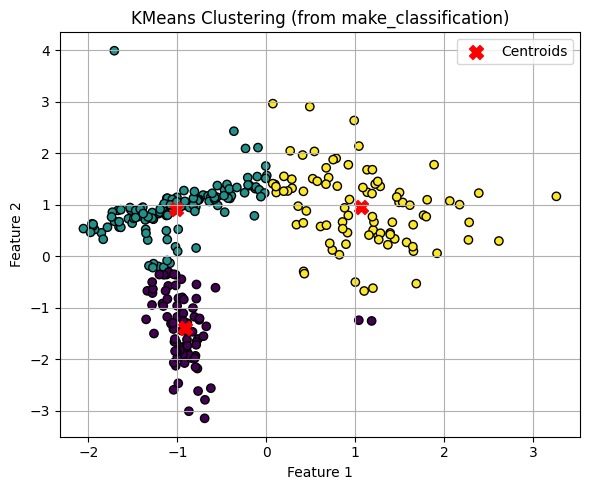
KMeans 클래스로 수행할 수 있고 n_clusters 로 cluster의 개수를 hyper parameter로 전달할 수 있다.
이제 fit_predict로 학습을 수행한 후에 예측 배열을 받을 수 있으며 kmenas.cluster_centers_ 를 이용해 centroid들의 위치를 얻을 수 있다.
다음은 Kmeans랑 DBSCAN의 차이이다.
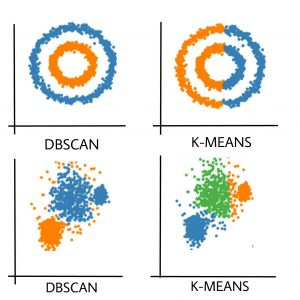
이미지 출처: https://syj9700.tistory.com/40
DBSCAN clustering algorithmPermalink
Density-Based Spatial Clustering of Applications with Noise의 준말이다.
DBSCAN은 Density-Based의 noise를 이용한 spatial clustering이다.
이상치를 검출하는데 좋은 알고리즘이며 독단적으로 Data Points들의 밀도에 기반해서 Clustering을 수행한다.
이상하게 생긴 데이터를 다루는데에 K-means보다 좋은 알고리즘이다.
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import DBSCAN
# 군집 형태 데이터 생성
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=42)
# DBSCAN 적용
db = DBSCAN(eps=1, min_samples=5)
labels = db.fit_predict(X)
# 시각화
plt.figure(figsize=(6, 5))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', edgecolor='k')
plt.title("DBSCAN Clustering (make_blobs)")
plt.tight_layout()
plt.show()
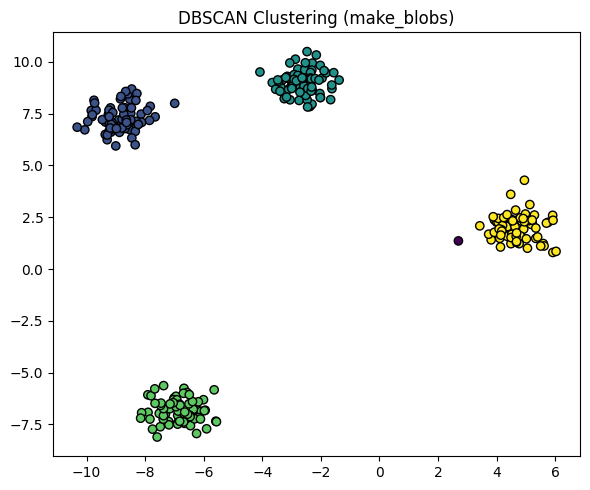
마찬가지로 sklearn.cluster에서 DBSCAN 클래스를 이용해 수행할 수 있고 fit_predict로 마찬가지로 예측한다.
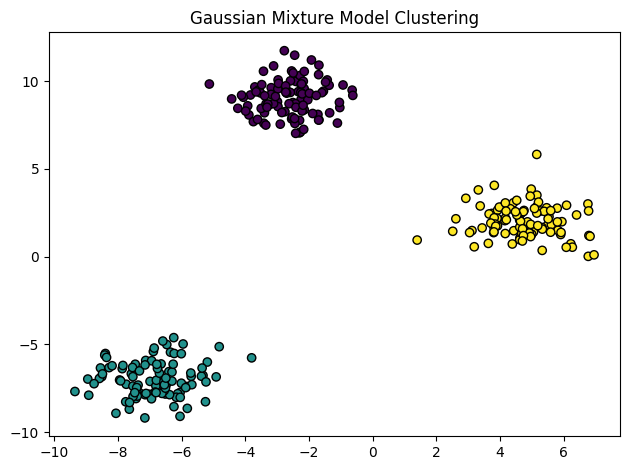
Gaussian Mixture Model algorithmPermalink
K-means의 문제중 하나는 데이터가 circular format을 따라야 한다는 점이다. K-means는 data points들의 거리 계산을 하기위해 circular path를 사용한다.
circular format은 주기적 값(0과 max가 연결된 구조)를 의미하며 주로 삼각함수를 이용해 데이터를 원형 구조로 해석하는 표현 방식이다. 선형 방식으로 데이터를 다루면 왜곡될 우려가 있는 경우에 사용된다.
Gaussian Mixture는 이 문제를 해결할 수 있다. Gaussian Mixture는 Circular format data를 필요로 하지 않는다.
Gaussian Mixture는 Gaussian Distributions를 이용해 독단적인 모양의 데이터를 다룬다.
여러가지의 이 Hybrid 모델에 대해서 숨겨진 레이어로 작동하는 single Gaussian model들이 있다.
따라서 모델은 data point가 어디 cluster에 속하는지에 대해 설정된 Gaussian distribution에 의해 확률을 결정한다.
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.mixture import GaussianMixture
# 데이터 생성
X, _ = make_blobs(n_samples=300, centers=3, cluster_std=1.0, random_state=42)
# GMM 모델 학습
gmm = GaussianMixture(n_components=3, covariance_type='full', random_state=42)
gmm.fit(X)
# 클러스터 예측
labels = gmm.predict(X)
# 시각화
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', edgecolor='k')
plt.title("Gaussian Mixture Model Clustering")
plt.tight_layout()
plt.show()
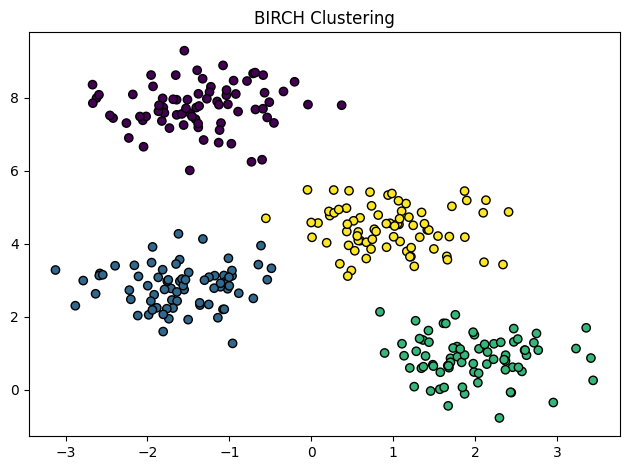
BIRCH algorithmPermalink
Balance Iterative Reducing and Clustering using Hierarchies 의 준말이다.
data들을 Clusters인 little summaries로 변환한다. Summaries는 가능한 Data Point에 대한 Distribution Information을 많이 갖게된다.
이 알고리즘은 흔하게 다른 Clustering 알고리즘들과 같이 쓰이는데, 다른 Clustering Techniques들이 BIRCH로 만들어진 Summaries들을 기반으로 작동하면 더 효율적이기 때문이다.
BIRCH의 주 단점은 Numeric Data values들로만 학습이 될 수 있다는 점이다.
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import Birch
# 데이터 생성
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=0)
# BIRCH 모델 학습
birch = Birch(n_clusters=4)
labels = birch.fit_predict(X)
# 시각화
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', edgecolor='k')
plt.title("BIRCH Clustering")
plt.tight_layout()
plt.show()
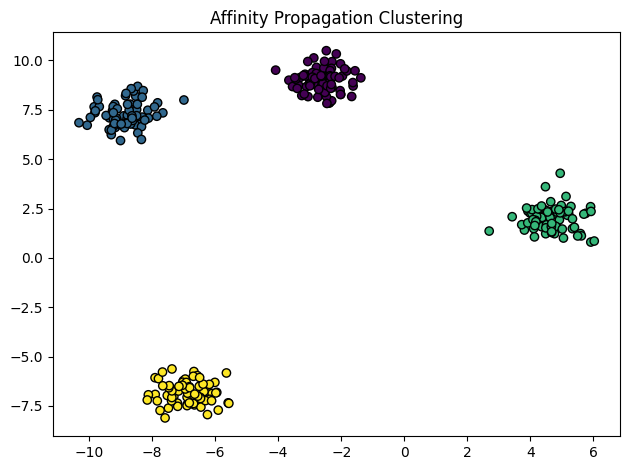
Affinity Propagation Clustering AlgorithmPermalink
이 알고리즘은 다른 기법들과 전혀 다른 방식을 취한다.
각 Data points는 다른 모든 data points들과 그들이 서로 얼마나 유사한지에 대해서 소통하고 군집을 형성할 것인지 결정한다.
알고리즘에게 Clusters의 개수를 사전에 알려줄 필요가 없다.
Data points들간 메세지가 주고받아지면 exemplars 라는 data의 집합들이 찾아지고 그것이 cluster를 구성한다.
DBSCAN처럼 초기 군집수를 결정해줄 필요 없으므로 Computer Vision문제 같은곳에 적합하다.
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import AffinityPropagation
# 데이터 생성
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=42)
# Affinity Propagation 적용
ap = AffinityPropagation(damping=0.9, preference=-50, random_state=0)
labels = ap.fit_predict(X)
# 시각화
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', edgecolor='k')
plt.title("Affinity Propagation Clustering")
plt.tight_layout()
plt.show()
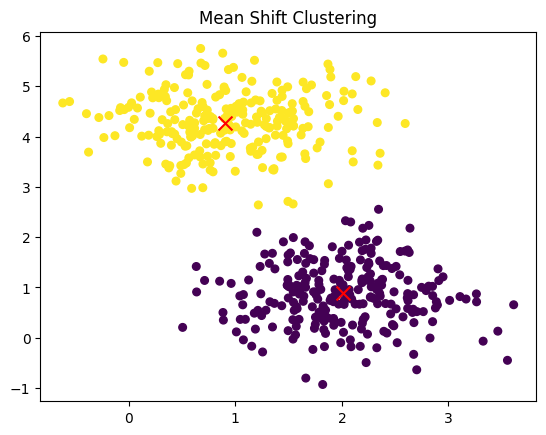
Mean-Shift clustering algorithmPermalink
이 알고리즘도 image와 computer vision 프로세싱에 좋은 알고리즘이다.
BIRCH, DBSCAN, Affinity Propagation와 비슷하게 초기 cluster 개수 없이 진행된다.
이 알고리즘은 Hierarchical Clustering이지만 큰 데이터 셋에선 잘 동작하지 않는다.
Mean-Shift는 모든 Data Point를 반복하며 최빈값으로 data point들을 Shift 시킨다. 이 맥락에서 Mode란 Region에서 Data Point들이 높은 밀도로 모여있는 것을 의미한다.
당신은 이 알고리즘을 Mode-Seeking 알고리즘이라고도 들어봤을 것이다.
모든 data points들이 cluster에 할당될 때까지 반복된다.
from sklearn.datasets import make_blobs
from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
# 데이터 생성
X, _ = make_blobs(n_samples=500, centers=2, cluster_std=0.6, random_state=0)
# MeanShift 모델 생성 및 학습
ms = MeanShift()
ms.fit(X)
# 클러스터 결과
labels = ms.labels_
centers = ms.cluster_centers_
# 시각화
plt.scatter(X[:, 0], X[:, 1], c=labels, s=30)
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='x', s=100)
plt.title("Mean Shift Clustering")
plt.show()
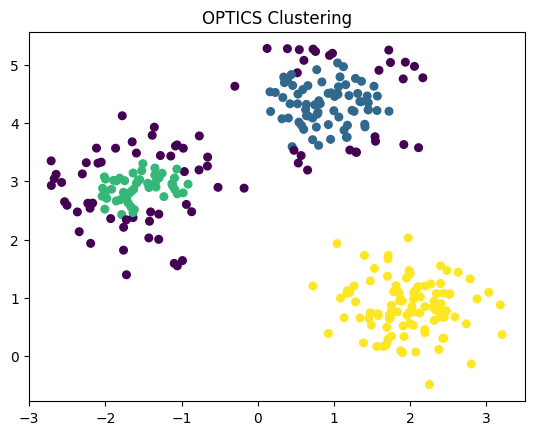
OPTICS AlgorithmPermalink
OPTICS는 Ordering Points to Identify the Clustering Structure의 준말이다.
Density-Based Algorithm이다.
DBSCAN과 비슷한데 Density가 상이한 meaningful clusters를 찾는데 더 적합하다.
Data points들을 ordering해서 ordering에서 인접한 data points들끼리 Clusters를 형성한다.
DBSCAN이랑 유사하지만 더 느리고 모든 data point를 한 번씩만 검사한다.
각 data point에서 각 cluster 별로 속하는 것을 의미하는 특별한 거리들을 저장한다.
- 클러스터수를 자동으로 지정한다.
eps는 최대 거리 제한이다.min_samples이상 이웃이 있으면 핵심 포인트로 간주한다.
from sklearn.datasets import make_blobs
from sklearn.cluster import OPTICS
import matplotlib.pyplot as plt
# 데이터 생성
X, _ = make_blobs(n_samples=300, centers=3, cluster_std=0.5, random_state=0)
# OPTICS 모델 학습
optics = OPTICS(min_samples=15)
optics.fit(X)
# 결과 추출
labels = optics.labels_
reachability = optics.reachability_
# 시각화
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=30)
plt.title("OPTICS Clustering")
plt.show()
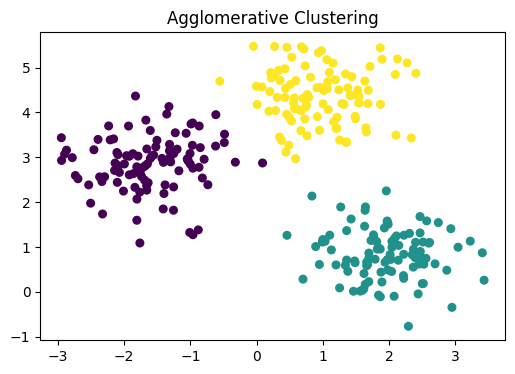
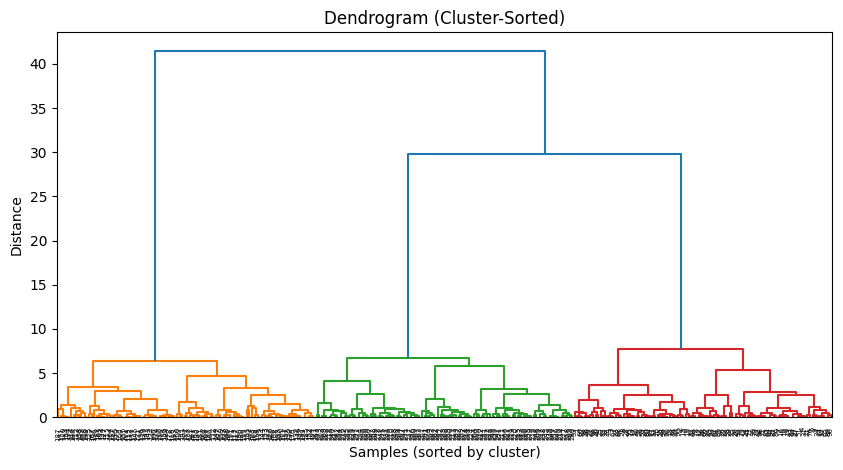
Agglomerative Hierarchy Clustering AlgorithmPermalink
Hierarchical Clustering Algorithm중 가장 많이 쓰인다.
data들을 그들이 서로 얼마나 유사한지에 대해 기반으로 그루핑한다.
bottom up clustering의 형태이며 처음엔 data point들이 cluster로 묶이고, 그 clusters들이 서로 또 cluster를 형성하는 계층적 구조이다.
각 iteration마다, 유사한 cluster들이 모든 data point들이 하나의 큰 root cluster가 될 때 까지 merge된다.
Agglomerative clustering은 작은 clusters들을 찾는데 가장 좋다.
덴드로그램처럼 결과가 나오며 쉽게 visualization 하기도 좋다.
from sklearn.datasets import make_blobs
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import dendrogram, linkage
import matplotlib.pyplot as plt
import numpy as np
# 데이터 생성
X, _ = make_blobs(n_samples=300, centers=3, cluster_std=0.6, random_state=0)
# Agglomerative Clustering 모델 학습
agg = AgglomerativeClustering(n_clusters=3)
labels = agg.fit_predict(X)
# 클러스터링 시각화
plt.figure(figsize=(6, 4))
plt.scatter(X[:, 0], X[:, 1], c=labels, s=30)
plt.title("Agglomerative Clustering")
plt.show()
# 덴드로그램 시각화 (클러스터링 결과에 맞춰서 정렬)
linked = linkage(X, method='ward')
# 샘플 순서를 클러스터별로 정렬
order = np.argsort(labels)
X_sorted = X[order]
linked_sorted = linkage(X_sorted, method='ward')
plt.figure(figsize=(10, 5))
dendrogram(linked_sorted)
plt.title("Dendrogram (Cluster-Sorted)")
plt.xlabel("Samples (sorted by cluster)")
plt.ylabel("Distance")
plt.show()
Other types of clustering algorithmsPermalink
8가지의 자주 쓰이는 clustering algorithms 들을 알아보았다.
그러나 여러가지 다른것도 존재한다.
bottom up으로 진행되는 agglomerative clustering algorithm과 상반되는 top down으로 진행되는 Divisive Hierarchical clustering algorithm도 있다.
Mini-Batch K-means는 K-means와 비슷하지만 고정된 크기의 작은 랜덤한 데이터의 chunk를 사용해서 메모리에 저장될 수 있다는 점이 다르다. 이는 K-means를 더 빠르게 결과에 수렴시키는데 도움을 준다.
이 알고리즘의 단점은 빠르게 수렴하는대신 정확도가 떨어질 수 있다는 것이다.
Spectral Clustering은 Graph를 이용해 처음에 데이터에 아무런 추측도 하지않고 data point를 graph에서 하나의 node로 간주하고 edge로 이어진 노드들끼리의 모임을 기반으로 클러스터링을 진행한다.
Other thoughtsPermalink
Clustering Algorithm들 중에는 data point를 방식으로 하나하나 비교하는 방식도 있기 때문에 백만개 이상의 데이터가 들어올 시에 학습이 일반적인 성능의 컴퓨터로 불가능해질 수 있음도 유의해야 한다.



Comments