Codeforces Round 876 (Div. 2)

A. The Good ArrayPermalink

A. The Good Array

그리디하게 $1, k+1, 2k+1$ 에 $1$을 채워넣는 것이 좋다.

$i$ 를 채워넣을 때, $n+1-i$ 도 $1$로 채운다.

$i$를 $1$부터 $\left\lceil \dfrac{n}{2} \right\rceil$ 까지 순회한다.

이제 $i$ 를 다시 $1 \to n$ 까지 보면서 어떤 $i$에 대해 $\left\lceil \dfrac{i}{k} \right\rceil$ 가 현재까지 합보다 많은 경우에는 정답에 $+1$ 을 해준다.

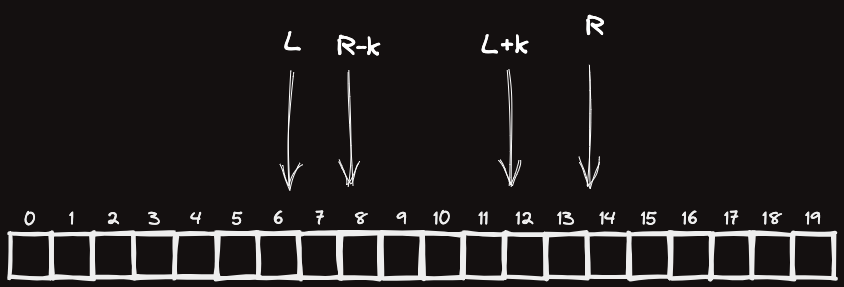
그건 위 그림과 같은 경우이고 중간에 무조건 $1$하나를 끼워넣어서 정답을 만들 수 있기 때문이다.

$O(1)$ 풀이Permalink

$N \ge 2$이고 $a_1=a_n=1$ 으로 둬야한다.

$\left\lceil \right\rceil$ 를 집어치우고 $\left\lfloor \right\rfloor$로만 따져보자.

$1, k+1,2k+1,\cdots$ 처럼 되므로 $1$ 을 미리 포함시켜 줘버린다면

$k, 2k, \dots$ 처럼 배열에 $1$ 이 찍히는 것과 다름없다.

$a_1=a_n=1$ 으로 미리 빼버렸으므로 남은 배열의 길이는 $n-2$ 이고 따라서 $\left\lfloor \dfrac{n-2}{k} \right\rfloor+2$ 가 정답이다.

left to right는 그렇다 치고 왜 right to left도 가능할까?

왼쪽에서 $a_1,a_{k+1}$ 사이의 거리는 $k$ 인데, 오른쪽에서 $a_n,a_{k \cdot \left\lfloor \frac{n-2}{k} \right\rfloor +1}$ 사이의 거리는 항상 $k$ 이하이기 때문이다.

$n-\left( k\left\lfloor \dfrac{n-2}{k} \right\rfloor+1\right)$는 $n=qk+1$ 일 때 최대고, 식을 풀면

이여서 최대 $k$ 이다. $\square$

B. LampsPermalink

B. Lamps

$a_i$ 가 작은 순서대로 램프를 킨다고 생각하자.

broken 된 것은 $x$의 개수에 포함되지 않으므로, 항상 $a_i$ 가 동일한 것의 개수가 $A$ 개일 때, 최대 $\text{Min}(A,a_i)$ 개의 램프를 킬 수 있다.

그리디하게 $b_i$가 큰 것부터 키고 그것이 $a_i$ 개가 됐다면 이제 $a_i$ 를 가진 램프들은 모두 부숴지고 $x \coloneqq 0$ 으로 초기화된다.

만약 $A < a_i$ 라서 모든 $a_i$ 를 가진 램프를 킬 수 있다면, 어떤 $a_j > a_i$ 가 있어 $a_j$ 를 가진 램프들을 킨다고 생각하자.

이제 어떠한 시점에 $A + a_j$에서 킨 개수가 $a_i$ 가 되어 $x \coloneqq a_j$에서 킨 개수로 초기화가 된다.

즉, $a_i$ 가 다르다면 서로 영향을 미칠수 없다.

따라서 동일한 $a_i$ 램프들을 모아두고 $b_i$ 를 내림차순하여 $\text{Min}(A, a_i)$ 개를 뽑아 $b_i$들을 정답에 더해준다.

C. Insert Zero and Invert PrefixPermalink

C. Insert Zero and Invert Prefix

결론적으로 가장 뒤가 $0$이 아니면 항상 만들 수 있다.

$1 1 \cdots 1 1 0$ 는 항상 만들 수 있다.

$\underbrace{ 11\cdots11 }_{ x\text{개} }0$ 가 있다면 $x$ 개의 $0$을 $p=0$ 을 골라 추가한다음에 $p=x$ 를 골라 $x$개의 $0$들을 모두 $1$로 바꿔주면 된다.

그 이후 왼쪽에 다시 $0$이 나오는 것은 위에서 만든 구간과 독립적으로 동일하게 만들어줄 수 있다.

이를 관찰하는건 쉽고 이 생각을 잘 구현해야 하는 constructive 문제이다.

나는 앞에서부터 보면서 답을 구성하고 뒤집어 출력했다.

D. Ball SortingPermalink

D. Ball Sorting

문제를 보자마자 LIS가 떠올라 LIS에 포함되지 않은 것들을 최대한 그리디하게 $k$개의 $0$을 붙여 어떻게 정답을 구하려고 했으나 실패했다.

문제를 못 푼 원인은 다음과 같다.

1. LIS를 만드는 방법은 유일하지 않은데, 유일하지 않은 LIS의 형태로 고정된 답을 구하려 했다.
2. $k$가 커질수록 어느 시점부터 정답이 항상 $N-\vert LIS \vert$가 된다는 성질을 알아낸 것에 생각이 매몰되어 다른 풀이법을 탐색하지 못했다.

풀이는 다음과 같다.

LIS를 고려해야 하는 문제인건 맞는데, 그것에서 아이디어만 차용하는 방식이다.

무작위 순서의 길이 $N$의 배열 $A$가 있을 때, 임의의 원소들을 원하는 위치로 보내 정렬시킬 수 있는 최소 연산 횟수는 $N-LIS(A)$이다.

실제 어떤 원소들이 LIS에 포함되는지, 그렇지 않아서 옆에 $0$을 붙여 빠르게 올바른 위치로 보내줘야 하는지와 관계없이, DP를 정의해 일반적으로 문제를 해결하려 해보자.

$c=0$ 인 공을 붙인다는 것은 어떤 연속적인 구간을 원하는 위치로 이동시킬 수 있다는 말이다.

이 말은 이 연속적인 구간을 지워줄 수 있다는 말과 동치이다.

문제들에서 그리디한 결론에 의해 수열을 $x$ 개의 구간으로 나눠서 ~ 같은 테크닉은 꽤나 흔하니 염두해두자.

$c=0$ 인 공이 $k$ 개 있을 때, $k$ 개의 구간들을 선택하며 선택되지 않은 다른 구간들을 모두 모으면 증가수열인 경우의 증가수열의 최장 길이를 구하는 문제가 된다.

$DP[i][j]=i$ 번째 원소까지만 보며, 증가수열의 길이가 $j$이고, $i$ 번째 원소를 증가 수열의 마지막 원소로 포함할 때, 증가수열에 포함되지 않는 구간의 최소개수

이렇게 정의하면 답을 바로 구할수있는건 아니지만 테이블을 모두 채우고 $DP[i][j]=x$ 라 함은 길이 $j$인 증가수열이 $x$ 개의 공을 필을 필요로 한다는 것이기 때문에 $k=x$ 일 때의 정답을 $N-j$ 로 업데이트 해줄 수 있다.

단, $i \neq N$ 일 경우 $i$ 오른쪽 구간도 하나의 $c=0$ 인 공을 두는 것으로 쳐야하기 때문에 $k=x+1$ 일 때의 정답을 업데이트 해줌이 옳다.

아이보리님의 코드를 많이 참고했다.

void solve() {  
   int n;  
   cin >> n;  
   vi c(n + 1);  
   fv1(c);  
   vvi dp(n + 1, vi(n + 1, 1e9));  
  
   dp[1][1] = 0;  
   for (int i = 2; i <= n; i++) {  
      dp[i][1] = 1;  
      for (int j = 1; j <= i; j++) {  
         for (int k = 1; k < i; k++) {  
            if (c[k] < c[i]) {  
               if (k == i - 1)  
                  mina(dp[i][j], dp[k][j - 1]);  
               else  
                  mina(dp[i][j], dp[k][j - 1] + 1);  
            }  
         }  
      }  
   }  
   vi ans(n + 1, 1e9);  
   for (int i = 1; i <= n; i++) {  
      for (int j = 1; j <= i; j++) {  
         int need = dp[i][j];  
         if (i != n) need++;  
         if (need <= n)  
            mina(ans[need], n - j);  
      }  
   }  
   for (int i = 1; i <= n; i++) mina(ans[i], ans[i - 1]);  
   for (int i = 1; i <= n; i++) cout << ans[i] << ' ';  
   cout << endl;  
}

E. Decreasing GamePermalink

E. Decreasing Game