Codeforces Round 875 (Div. 1) - C. Hyperregular Bracket Strings (2400)

C. Hyperregular Bracket Strings

문제에 올바르게 접근했으나 구현에도 아이디어가 필요한 문제였다.

우선, 카탈란 수를 쓰는 문제임을 알 수 있다.

$C_n=\dfrac{1}{n+1}\dbinom{2n}{n}$ 이므로 전처리해 $O(1)$에 구할 수 있도록 한다.

regular bracket의 여러 조건들 중 구간이 짝수가 아니면 안되기 때문에

$2 \nmid n$ 혹은 $2 \nmid r_i-r_l+1$ 인 경우는 모두 정답이 $0$ 이다.

어떤 구간이 완전히 포함되게 겹치는 경우를 고려한다.

빗금친 구간도 regular bracket 이므로 구간의 길이가 짧은게 $a$ 긴게 $b$라면

정답은 $C_{a/2} \cdot C_{(b-a)/2}$ 임을 알 수 있다.

부분적으로 겹치는 경우를 고려한다.

이 때 겹치는 구간의 길이를 $c$ 라고 한다면

$2 \nmid c$ 라면 이또한 정답이 불가능함을 관찰할 수 있다.

왜냐면 $a$ 에선 저구간에서 balance가 $0$ 이상이고 $b$ 에선 저 구간에서 balance가 $0$ 이하여야 하기 때문에 정확히 저 구간도 regular bracket이 되어야 하고 결국 정답은 $C_{(a-c)/2}C_{(b-c)/2}C_c$ 이다.

이제 이 아이디어를 이용해 모든 구간을 어떻게 구현하여 처리할지가 관건이고, 여기서 막혔다.

이러한 구간은 트리의 형태를 띈다.

하지만 실제로 트리를 구현할 필요는 없다.

나는 이걸 구현을 prefix sum을 이용해서 어찌저찌 해보려 했는데, 에디토리얼에선 XOR Hashing이라는 기법을 소개한다.

각 구간에 대해 랜덤한 값 $v_i$를 할당하고, $l_i$ 에 $v_i$ 와 xor 하고, $r_i$ 에 $v_i$와 xor을 해서 imos법처럼 사용한다. 이 배열을 diff라고 한다면

그럼 이제 $\oplus_{i=0}^j \text{diff}(j)$ 가 인덱스 $j$ 가 속하는 구간의 해시이다.

일단 구간이 하나라면 두 지점 말고 다른 곳은 $0$ 으로 시작해서 prefix $\oplus$ 합이 구해지므로 그럴 것이다.

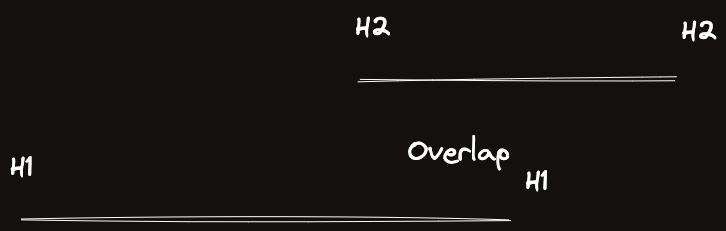
H1가 시작하는 부분부터 H2 가 시작하는 부분까지는 값이 H1일 것이다.

Overlap부분은 $H1 \oplus H2$ 가 된다.

이제 $H1$가 끝나는 부분부터 $H2$ 가 끝나는 부분까지는 $H2$ 가 된다. 옳게 처리가 되는 것을 알 수 있다.

이 경우도 동일함을 쉽게 알 수 있다.

따라서 각 해시가 나오는 빈도를 freq 라는 것에 저장하고 모든 구간들에 대해 카탈란수를 계산해주면 된다.

나오는 빈도가 홀수라면 불가능하므로 $0$ 을 출력한다.

struct _random {  
   mt19937 gen;  
   _random() : gen((unsigned) chrono::steady_clock::now().time_since_epoch().count()) {}  
   template<class T = int>  
   T nextInt(T l = 0, T r = 32767) { return uniform_int_distribution<T>(l, r)(gen); }  
   double nextDouble(double l = 0, double r = 1) { return uniform_real_distribution<double>(l, r)(gen); }  
} rd;  
const int inf = LLONG_MAX;  
const int MAX = 6e5;  
const ll mod = 998244353;  
int C[MAX + 5];  
inline ll md(ll x) { return md(mod, x); }  
vector<ll> fac(MAX + 1, 1LL), inv(MAX + 1);  
array<ll, 3> gcdx(ll A, ll B) {  
   ll x1 = 1, x2 = 0, y1 = 0, y2 = 1, r1 = A, r2 = B;  
   while (r2) {  
      ll q = r1 / r2;  
      if (r1 - r2 * q < 0) q--;  
      tie(x1, x2) = mp(x2, x1 - x2 * q);  
      tie(y1, y2) = mp(y2, y1 - y2 * q);  
      tie(r1, r2) = mp(r2, r1 - r2 * q);  
   }  
   return {x1, y1, r1};  
}  
inline int mdinv(int x) { return md(gcdx(x, mod)[0]); }  
ll bino(int i, int j) {  
   if (j > i) return 0LL;  
   return md(mod, md(mod, fac[i] * inv[j]) * inv[i - j]);  
}  
void pre_calc() {  
   for (int i = 2; i <= MAX; i++) fac[i] = md(mod, fac[i - 1] * i);  
   inv[MAX] = gcdx(fac[MAX], mod)[0];  
   for (int i = MAX - 1; i >= 0; i--) inv[i] = md(mod, inv[i + 1] * (i + 1));  
  
   // compute catalan numbers  
   C[0] = 1;  
   for (int i = 1; i <= MAX / 2; i++) {  
      C[i] = md(mdinv(i + 1) * bino(2 * i, i));  
   }  
}  
  
void solve() {  
   int n, k;  
   cin >> n >> k;  
   vector<pi> a(k);  
   map<int, int> freq;  
   vi diff(n + 1);  
   for (auto &[l, r]: a) cin >> l >> r, l--, r--;  
   {  
      // edge cases  
      if (n % 2) {  
         cout << 0 << endl;  
         return;  
      }  
      for (auto &[l, r]: a) {  
         if ((r - l + 1) % 2) {  
            cout << 0 << endl;  
            return;  
         }  
      }  
      if (k == 0) {  
         cout << C[n / 2] << endl;  
         return;  
      }  
   }  
   a.pb({0, n - 1});  
   k++;  
   for (int i = 0; i < k; i++) {  
      int h = rd.nextInt(0ll, inf - 1);  
      diff[a[i].fi] ^= h;  
      diff[a[i].se + 1] ^= h;  
   }  
   for (int i = 1; i <= n; i++) diff[i] ^= diff[i - 1];  
   for (int i = 0; i < n;) {  
      int h = diff[i], j = i;  
      while (j < n && diff[j] == diff[i])j++;  
      freq[h] += j - i;  
      i = j;  
   }  
   int ans = 1;  
   for (auto &[h, cnt]: freq) {  
      if (cnt % 2 == 1) {  
         cout << 0 << endl;  
         return;  
      }  
      ans = md(ans * C[cnt / 2]);  
   }  
   cout << ans << endl;  
}