Catalan Number

카탈란 수는 $n+1$개의 인수의 곱을 결합법칙이 성립하지 않을 때 표현하는 경우의 수이다.

$\quad \color{salmon} C_n$와 같이 쓴다.

예시로, $n=3$이면 다음과 같이 5개이다.

  1. $(((ab)c)d)$
  2. $((a(bc))d)$
  3. $(a((bc)d))$
  4. $(a(b(cd)))$
  5. $((ab)(cd))$

두 개씩만 인수들을 묶는다.

이 숫자가 재밌는 이유는, 위와 같이 겉보기엔 단순해보이는 정의가 나타내는 이 수가 굉장히 다양한 문제의 해답으로 표현되기 때문이다.

일반항

$C_0$을 $0$이라고 한다면,

$\quad C_n=1,~1,~2,~5,~14,~42,~132,~429,~1430,~4862,~\cdots$

와 같이 증가한다.

$\quad C_n= \dfrac 1{n+1} \dbinom{2n}n= \dfrac{(2n)!}{(n+1)!\cdot n!}$

이 일반항은 $O(N+\log p)$이 걸리지만, 실제로 수가 커져서 modular inverse를 계산하게끔 나머지를 소수로 주어지는 문제가 아니라면 써먹을 수 없는 방법이다.

$\quad C_n=\dfrac{2(2n-1)}{n+1}C_{n-1} \small (n\geq1)$

이 일반항은 $O(N \log p)$ 정도가 걸린다.

$\quad C_n=\displaystyle\sum_{k=0}^{n-1}C_k C_{n-1-k}=C_0 \cdot C_{n-1} + C_1 \cdot C_{n-2} + \cdots$

$O(N^2)$ 이지만 이것이 문제에서 가장 흔하다.

Applicable Problems

위에서 들었던 예시대로 문제를 풀어보자.

괄호, 스택 문제

BOJ 10422

이 문제는 $O(N^2)$로 해결할 수 있다.

괄호가 1쌍이라면, $()$ 정답은 1개이다.

2쌍이라면 $()()$, $(())$ 2개이다.

그 이후부터 생각을 해보자.

이번에 추가해야 할 괄호 한 쌍이 $()$ 처럼 있고, $(A)B$ 처럼 $A$와 $B$자리를 만들자.

남은 $N-1$ 쌍 중, $A$에 $K$쌍을 넣으면 $B$에는 $N-1-K$쌍이 존재하게 된다.

이는 곧 $C_{K} \cdot C_{N-1-K}$ 를 의미하며, 전체를 모두 합치면

$\quad C_n=\displaystyle\sum_{k=0}^{n-1}C_k C_{n-1-k}$ 이 된다.

이건 꼭 괄호라는 매개체만 적용되는 것이 아닌, 스택과 관련된 총 경우의 수라든가,

가령 Dyck words 같은 문제라든지,

다음과 같이 스택 문제로 환원될 수 있는 문제 같은 것들이 있다.

image

/ 모양과 \ 모양을 이용해 산을 만들 때 모양의 가지 수

다각형 분할

선분끼리 겹치지 않고 $n$각형일 때, $n-2$개의 영역으로 나누는 경우의 수

위 문제를 생각해보면, 6각형이므로 꼭짓점들을 $p_1,~\cdots~p_6$ 이라 한다면, $p_i$와 $p_j$를 이어 공간을 나눴을 때 $\small(\vert i - j \vert > 1)$, 나뉘어진 두 다각형에 있는 꼭짓점들의 개수가 $k+2,~6-k+2$가 됨이 보인다.

예를 들어 육각형의 두 인접하지 않는 꼭짓점을 이어 삼각형과 오각형으로 분할할 수 있다.

$\quad C_6=C_3 \cdot C_5 + C_4 \cdot C_4 + C_5 \cdot C_3$ 가 되고,

여기서 2씩 빼면 카탈란 수의 점화식이 나옴을 볼 수 있을 것이다.

악수 문제

BOJ 17268, BOJ 1670

각 꼭짓점들이 짝지어 겹치지 않는 경우가 몇개가 나오는지를 묻는 문제이다.

동일하게 카탈란 수로 풀 수 있다.

$N, N$ grid에서 대각선을 넘어가지 않고 한 쪽 영역만 사용해서 이동하는 최단경로 문제

image

이 문제에서 $C_N=\dfrac 1{2n+1} \dbinom{2n}n$ 을 증명할 것이다.

위 문제에서 대각선을 넘어가지 않고 한쪽 영역만으로 반대쪽 대각선 꼭짓점에 도달하는 경로의 수는 앞서 다루었던 문제들로 치환될 수 있기 때문에 이러한 경로의 개수가 $\dfrac 1{2n+1} \dbinom{2n}n$ 라고 증명하면 된다. (전단사 증명)

exceedance = 대각선 위에있는 수직경로의 개수

라고 하자.

예를 들어 다음과 같은 그림은 exceedance가 5이다.

만약 exceedance가 $0$이 아닌 어떤 경로가 있다면, 다음과 같은 알고리즘을 통해 exceedance를 $1$ 줄여줄 수 있다.

  1. 왼쪽 아래에서 시작해 diagonal(대각선 그어져있는 것) 위에 도달할 때 까지 진행
  2. digonal을 두 번째로 touch 할 때, 그 때의 $x$좌표를 $X$라 하자.
  3. $[0,\,X-1]$와 $[X,\,N]$ 구간의 경로를 Swap 한다.

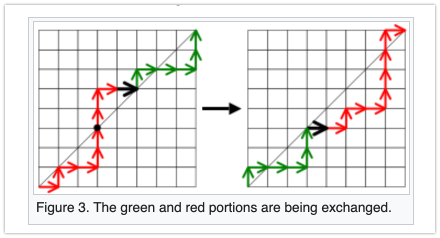
exceedance는 $3\to2$ 이다.

이것이 성립하는 이유는 일단 앞으로간 $[X,\,N]$에서의 exceedance는 변함이 없고

$[X,\,X]$를 시작해$[N,\,N]$ 을 거치던 경로가 $[0,\,0]$에서 시작해 $[N-X,\,N-X]$로 옮겨진 것이기 때문이다.

뒤로간 $[0,\,X-1]$ 의 경로는 항상 $\to$가(Figure의 검은색 화살표) 하나 먼저 붙은 채로 $X$에서 다시 시작하기 때문에 exceedance는 $1$ 감소한다.

이로 인해 얻을 수 있는 결론은,

$$ \quad exceedance_n=exceedance_{n-1}=\cdots=exceedance_0 $$

이다.

따라서 $n+1$ 개의 서로 다른 exceedance를 가지는 경로들의 개수가 모두 같고, 총 경로의 개수는 $\color{salmon} \dbinom{2n}n$ 이기 때문에,

$$ C_n=\dfrac1{n+1}\dbinom{2n}n $$

임이 증명된다.

구현

$O(N^2)$

$O(N^2)$부터 살펴보자.

BOJ 10422 를 풀어보자.

const ll mod = 1e9 + 7;  
inline ll md(ll x) { return md(mod, x); }  
void solve() {  
   int t;  
   cin >> t;  
  
   vector<ll> dp(2501);  
   dp[0] = 1;  
   for (int i = 1; i <= 2500; i++) {  
      for (int j = 0; j < i; j++) {  
         int k = i - 1 - j;  
         dp[i] = md(dp[i] + dp[j] * dp[k]);  
      }  
   }  
  
   while (t--) {  
      int n;  
      cin >> n;  
  
      if (n & 1) cout << 0 << endl;  
      else cout << dp[n / 2] << endl;  
   }  
}

와 같이 풀 수 있다. 식을 그대로 가져다 써주기만 하면 된다.

$O(N)$

$\quad C_n \equiv \dfrac 1{n+1} \dbinom{2n}n \equiv \dfrac{(2n)!}{(n+1)!\cdot n!}~~\small(mod~p)$

이제 이 식을 이용해보자.

우리가 먼저 계산해야 할건 $2n$ 까지에 대한 값이다.

vi f(5001);  
f[0] = 1;  
for (int i = 1; i <= 5000; i++) f[i] = md(f[i - 1] * i);

이제 $(n+1)! \cdot n!$ 의 모듈러 역원을 곱해주기만 하면 된다.

이는 페르마의 소정리

$$ a^{p-1} \equiv 1~~(mod~p)\\ \small (p \nmid a) $$

를 이용하여 모듈러 역원의 정의는 $a$ 에 대해 $ax\equiv1$ 를 만족하는 $x$ 이므로

$a\cdot a^{p-2}\equiv1~~(mod~p)\ \Rightarrow x=a^{p-2}$ 이용해서 푼다.

const ll mod = 1e9 + 7;  
inline ll md(ll x) { return md(mod, x); }  
  
ll pw(ll a, ll b) {  
   ll ret = 1;  
   while (b) {  
      if (b & 1) ret = md(ret * a);  
      a = md(a * a);  
      b >>= 1;  
   }  
   return ret;  
}  
  
void solve() {  
   int t;  
   cin >> t;  
  
   vector<ll> f(5001);  
   f[0] = 1;  
   for (int i = 1; i <= 5000; i++) f[i] = md(f[i - 1] * i);  
  
   while (t--) {  
      int n;  
      cin >> n;  
  
      if (n & 1) {  
         cout << 0 << endl;  
         continue;  
      }  
  
      n >>= 1;  
      ll ans = f[n * 2];  
      ll denomiator = md(f[n + 1] * f[n]);  
      ll inverse = pw(denomiator, mod - 2);  
  
      cout << md(ans * inverse) << endl;  
   }  
}

이렇게 다른 시간복잡도로 풀었을 때 결과는 다음과 같다.

Comments

You may also enjoy