Codeforces Round 874 (Div. 3)

May 20, 2023

A. Musical Puzzle

인접한 $s_i s_{i+1}$ 이 유일한 것의 개수를 세자.

B. Restore the Weather

정렬해서 올바르게 묶어주면 된다.

void solve() {
   int n, k;
   cin >> n >> k;
   vi a(n), b(n);
   fv(a);
   fv(b);
   vi idx(n);
   iota(all(idx), 0);
   sort(all(idx), [&](int i, int j) { return a[i] < a[j]; });
   sort(all(b));
   vi ans(n);
   for (int i = 0; i < n; i++) {
      ans[idx[i]] = b[i];
   }
   for (int i: ans) cout << i << ' ';
   cout << endl;
}

C. Vlad Building Beautiful Array

중복된 값을 없애고 정렬하고 순회하며 지금까지 나온 것 중 짝수나 홀수가 있었는지를 파악한다.

자신이 짝수이고 현재까지 홀수가 안나왔다면 모두 홀수가 될 수 없다.

마찬가지로 자신이 홀수이고 현재까지 홀수가 안나왔다면 모두 짝수가 될 수 없다.

마지막에 모두 홀수가 되거나 모두 짝수가 될 수 있는지만 검사해주면 된다.

void solve() {
   int n;
   cin >> n;
   vi a(n);
   fv(a);
   uniq(a);
 
   n = sz(a);
   if (n == 1) {
      cout << "YES\n";
      return;
   }
 
   int can_even = 1, can_odd = 1;
   int even = 0, odd = 0;
   for (int i = 0; i < n; i++) {
      if (a[i] % 2 == 0 && !odd) {
         can_odd = 0;
      }
      if (a[i] % 2 == 1 && !odd) {
         can_even = 0;
      }
 
      if (a[i] % 2 == 0) even = 1;
      else odd = 1;
   }
   if(can_even || can_odd) cout << "YES\n";
   else cout << "NO\n";
}
 

D. Flipper

몇가지 케이스를 나눠 모두 검사해보면 된다. $O(n^2)$ 으로 풀 수 있기 때문이다.

우선, 가장 큰 수가 가장 앞에 와야한다고 해보자.

가장 큰 수가 처음에 가장 앞에 와있으면 그렇게 만들 수 없다.

그럼 두 번째로 가장 큰 수가 가장 앞에 올 수 있는 대략 $O(n)$ 가지를 모두 검사해보는 것이다.

void solve() {
   int n;
   cin >> n;
   vi a(n);
   fv(a);
   for (int &i: a) i--;
   auto copy = a;
   int ni = maxi(a);
   vvi cand;
   reverse(all(a));
   cand.pb(a);
   a = copy;
 
   if (n == 1) {
      for (int i: a) cout << i + 1 << ' ';
      cout << endl;
      return;
   }
 
   if (ni == 0) {
      // 가장 앞에 있다면
      for (int i = 0; i < n; i++) if (a[i] == n - 2) ni = i;
      for (int l = (ni == n - 1 ? ni : ni - 1); l >= 0; l--) {
         a = copy;
         reverse(a.begin() + l, a.begin() + ni);
         vi b;
         for (int i = ni; i < n; i++) b.pb(a[i]);
         for (int i = l; i < ni; i++) b.pb(a[i]);
         for (int i = 0; i < l; i++) b.pb(a[i]);
         cand.pb(b);
      }
   } else {
 
      for (int l = 0; l < (ni == n - 1 ? ni + 1 : ni); l++) {
         a = copy;
         reverse(a.begin() + l, a.begin() + ni);
         vi b;
         for (int i = ni; i < n; i++) b.pb(a[i]);
         for (int i = l; i < ni; i++) b.pb(a[i]);
         for (int i = 0; i < l; i++) b.pb(a[i]);
         cand.pb(b);
         debug(b);
      }
   }
   sort(all(cand), greater<>());
   for (int i: cand[0]) cout << i + 1 << ' ';
   cout << endl;
}

E. Round Dance

그래프같긴 했는데 오늘은 Virtual로 풀어서 이건 못풀었다.

다시 생각해보았다.

근데 생각해보니 한 명만 기억하므로 아무런 사람 두 명 엮어서 그 두사람끼리 라운드를 진행했다고 하면 무한히 max를 늘릴 수 있는데 이 경우는 뭘까

씨팔출제자 description 인성어디

F. Ira and Flamenco

우선 수들을 정렬하고 이분탐색으로 현재 수가 $a_i$ 라고 한다면 $[a_i, a_i+m)$ 범위에 서로 다른 수가 몇개인지를 찾는다.

만약 그것이 $m$ 개 이상이라면 가능한 경우이다.

그런데 여기서 생각해보면 그것이 $m$ 개 초과가 될 수는 절대 없다는 것을 알 수 있다.

더 엄밀히 말하자면 저 범위에 수가 서로 다르려면 $a_{i+1}=a_i+1,~a_{i+2}=a_i+2, \dots$ 여야 한다는 것을 알 수 있다.

따라서 $[a_i,a_i+m)$ 범위에 모두 수가 있다면, 전처리해둔 각 수마다 나오는 횟수를 모두 곱해주고 정답에 더해주기만 하면 된다.

모두 곱해주는 방법은 구간곱 배열을 modular inverse를 이용해서 적절히 계산하여 $O(n \log n)$에 풀 수 있다.

const ll mod = 1e9 + 7;  
inline ll md(ll x) { return md(mod, x); }  
  
array<ll, 3> gcdx(ll A, ll B) {  
   ll x1 = 1, x2 = 0, y1 = 0, y2 = 1, r1 = A, r2 = B;  
   while (r2) {  
      ll q = r1 / r2;  
      if (r1 - r2 * q < 0) q--;  
      tie(x1, x2) = mp(x2, x1 - x2 * q);  
      tie(y1, y2) = mp(y2, y1 - y2 * q);  
      tie(r1, r2) = mp(r2, r1 - r2 * q);  
   }  
   return {x1, y1, r1};  
}  
int inverse(int x) {  
   return md(gcdx(x, mod)[0]);  
}  
  
template<class T>  
struct fenwick {  
   int n;  
   vector<T> tree;  
   fenwick(int n) : n(n) { tree.resize(n + 1); }  
   T sum(int i) {  
      T ret = 0;  
      for (; i; i -= i & -i) ret += tree[i];  
      return ret;  
   }  
   void update(int i, T x) { for (i++; i <= n; i += i & -i) tree[i] += x; }  
   T query(int l, int r) { return l > r ? 0 : sum(r + 1) - sum(l); }  
};  
  
  
void solve() {  
   int n, m;  
   cin >> n >> m;  
   vi a(n), can(n);  
   fv(a);  
   sort(all(a));  
  
   fenwick<int> fenw(n);  
  
   map<int, int> cnt;  
   for (int i = 0; i < n; i++) {  
      cnt[a[i]]++;  
      if (i == 0 || a[i] != a[i - 1]) {  
         can[i] = 1;  
         fenw.update(i, 1);  
      }  
   }  
  
   vi pmul(n + 1, 1);  
   for (int i = 0; i < n; i++) {  
      pmul[i + 1] = md(pmul[i] * (can[i] ? cnt[a[i]] : 1));  
   }  
   auto query = [&](int l, int r) {  
      return md(pmul[r + 1] * inverse(pmul[l]));  
   };  
  
   int ans = 0;  
   for (int i = 0; i < n; i++) {  
      if (!can[i]) continue;  
      int low = a[i];  
      int upper = a[i] + m - 1;  
      int j = ubi(a, upper) - 1;  
  
      int can_cnt = fenw.query(i, j);  
      if (can_cnt < m) continue;  
      ans = md(ans + query(i, j));  
   }  
   cout << ans << endl;  
}

G. Ksyusha and Chinchilla

귀찮은 구현문제인데, 에디토리얼은 tree dp를 말하지만, 다음과 같은 방법으로 풀었다.

결국 branch는 두 가지 형태만 나옴에 유의한다.

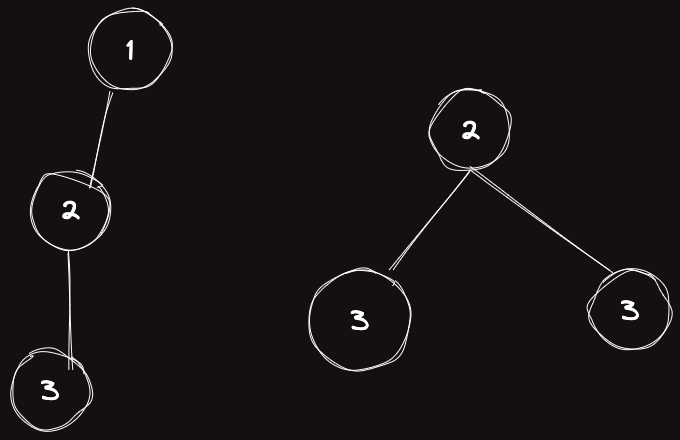
이처럼 각 브랜치의 노드마다 번호를 매겨보자.

처음에 모든 leaf 노드는 항상 $3$을 갖는다.

이제 자신이 $3$이라면 자신의 바로 부모는 $2$여야 하는 제약이 생긴다.

자신이 $2$인데 자식 중 $3$의 개수가 $2$개라면 그 두개와 자신으로 하나의 branch를 만들고, $1$개라면 그 하나와 자신의 부모와 branch를 만든다.

그 이외의 경우는 실패이다.

자신이 $1$이라면 자식 중 $3$은 없어야한다.

자신이 $1,2,3$ 셋다 아니라면 다시 자신을 $3$으로 만들어주고 leaf노드처럼 시작해주면 된다.

이처럼 과정을 진행후 모순이 없다면, branch에 쓰인 간선들을 모두 제외하면 잘라내야할 간선들만 남게된다.

void solve() {
   int n;
   cin >> n;
   vvi edges(n);
   map<pi, int> edge_idx;
   for (int i = 0, u, v; i < n - 1; i++) {
      cin >> u >> v, u--, v--;
      edge_idx[mp(min(u, v), max(u, v))] = i;
      edges[u].pb(v), edges[v].pb(u);
   }
   if (n % 3) {
      cout << -1 << endl;
      return;
   }
   int cut = n - 1 - n / 3 * 2;
   debug(n, cut);
   vi par(n), sub_size(n), in(n), type(n);
   vvi child(n);
   queue<int> q;
   function<void(int, int)> fn = [&](int i, int p) -> void {
      sub_size[i] = 1;
      par[i] = p;
      int c = 0;
      for (int j: edges[i])
         if (j != p) {
            in[i]++;
            fn(j, i), child[i].pb(j);
            sub_size[i] += sub_size[j];
            c++;
         }
      if (!c) {
         type[i] = 3;
         q.push(i);
      }
   };
   fn(0, -1);
   bool fail = 0;
   vi fin(n);
   map<int, set<int>> con;
   auto connect = [&](int i, int j, int k) {
      con[i].insert(j);
      con[j].insert(i);
      con[j].insert(k);
      con[k].insert(j);
   };
   while (sz(q)) {
      int i = q.front();
      q.pop();
 
      if (i == 0) {
         if (type[i] == 2) {
            vi type3child;
            for (int c: child[i]) if (type[c] == 3) type3child.pb(c);
            if (!sz(type3child) || sz(type3child) > 2) fail = 1;
            if (sz(type3child) == 1) {
               fail = 1;
            } else {
               fin[i] = fin[type3child[0]] = fin[type3child[1]] = 1;
               connect(type3child[0], i, type3child[1]);
            }
         } else if (type[i] == 1) {
            vi type3child;
            for (int c: child[i]) if (type[c] == 3) type3child.pb(c);
            if (sz(type3child)) fail = 1;
         }
         continue;
      }
      int p = par[i];
 
      if (type[i] == 3) {
         if (type[p] && type[p] != 2) fail = 1;
         type[p] = 2;
 
      } else if (type[i] == 2) {
         vi type3child;
         for (int c: child[i]) if (type[c] == 3) type3child.pb(c);
         if (!sz(type3child) || sz(type3child) > 2) fail = 1;
         if (sz(type3child) == 1) {
            if (type[p]) fail = 1;
            type[p] = 1;
            fin[i] = fin[type3child[0]] = fin[p] = 1;
            connect(type3child[0], i, p);
         } else {
            fin[i] = fin[type3child[0]] = fin[type3child[1]] = 1;
            connect(type3child[0], i, type3child[1]);
         }
      } else if (type[i] == 1) {
         vi type3child;
         for (int c: child[i]) if (type[c] == 3) type3child.pb(c);
         if (sz(type3child)) fail = 1;
      } else {
         type[i] = 3;
         if (type[p] && type[p] != 2) fail = 1;
         type[p] = 2;
      }
 
      in[p]--;
      if (in[p] == 0) q.push(p);
   }
   debug(fin);
   for (int i = 0; i < n; i++) if (!fin[i]) fail = 1;
 
   if (fail) cout << -1 << endl;
   else {
      vi ans;
      cout << cut << endl;
      function<void(int)> fn = [&](int i) -> void {
         for (int c: child[i]) {
            if (!hass(con[i], c)) {
               ans.pb(edge_idx[mp(min(i, c), max(i, c))]);
            }
            fn(c);
         }
      };
      fn(0);
      for (auto i: ans) cout << i + 1 << ' ';
      cout << endl;
   }
}
 

에디토리얼 풀이 1

$dpc_v=$ 서브트리 $v$에서 모든 자식으로 가는 간선을 자를 수 있다

$dpo_v=$ 서브트리 $v$에서 모든 자식으로 가는 간선 중 하나만 남기고 자를 수 있다.

$dp_v=$ 서브트리 $v$에서 부모로 가는 간선을 자를 수 있다.

처럼 정의하고 트리 DP를 쓰는 것이다.

명백히 해의 존재는 $dp_0$ 이 참일 경우이다.

에디토리얼 풀이 2

그리디로 풀 수 있다.

light vertex를 leaf가 아니고 자신의 모든 자식이 leaf인 vertex라고 정의한다.

heavy vertex를 leaf가 아니고 light vertex인 자식을 가지는 vertex라고 정의한다.

만약 light vertex 중 자식이 세 개 이상인 것이 있다면 정답은 존재하지 않는다.

만약 light vertex가 오직 하나의 자식을 갖는다면 우린 그것의 부모에서 light vertex만 남기고 모두 자른다.

만약 light vertex가 두 개의 자식을 갖는다면 light vertex에서 부모로 가는 간선을 자른다.

우선, 각 vertex의 자식의 개수와 light vertex인 자식의 개수를 센다.

light vertex를 계속 자르다보면 부모도 light vertex가 되는데, 그럼 큐에 넣는다.

이렇게 어쩌구 저쩌구해서 정답을 구할 수 있다는 것 같은데 내 풀이와 유사한 것 같다.

Codeforces Round 874 (Div. 3)

A. Musical Puzzle

B. Restore the Weather

C. Vlad Building Beautiful Array

D. Flipper

E. Round Dance

F. Ira and Flamenco

G. Ksyusha and Chinchilla

에디토리얼 풀이 1

에디토리얼 풀이 2

Comments

You may also enjoy

DaisyUI 공부 및 웹사이트에 적용

모집병 실시간 지원현황 웹사이트 개발

D3 공부, TailwindCss

241203 일상 - Next 복습