Codeforces Round 865 (Div. 2) - D. Sum Graph (2000)

D. Sum Graph

문제에 대한 감은 금방 잡았으나 까다로운 구현때문에 너무 많은 시간을 썼다.

내가 한 관찰은 다음과 같다.

$x=n, x=n+1$ 로 쿼리를 날리면

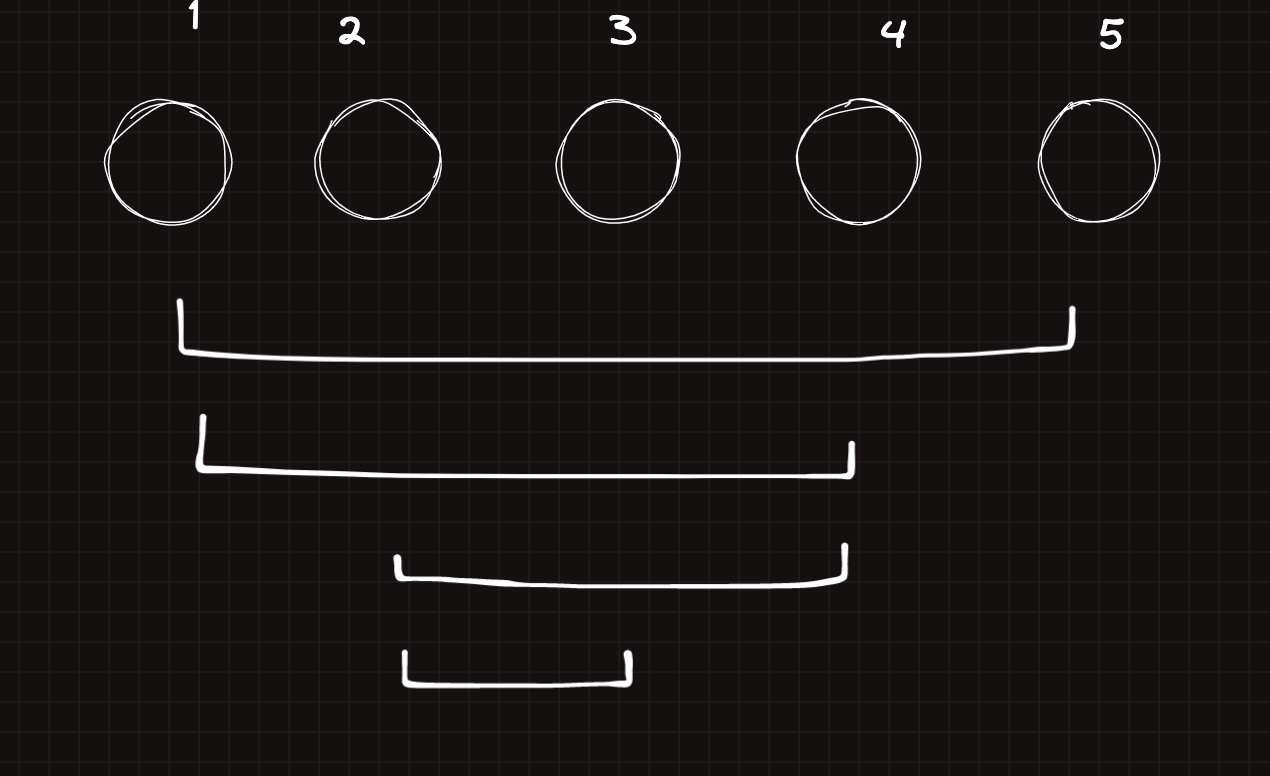
이런식으로 간선을 구성해줄 수 있고 체인을 형성한다.

그 체인은 $5-1-4-2-3$ 과 같은 순서이다.

항상 제일 오른쪽이 체인의 시작이라고 두면 parity에 관계없이 순서를 구성할 수 있다.

$i=1$에 대해 $2 \sim n$ 까지 모두 두 번째 쿼리를 날려주고 최단경로들을 모두 기록한다.

그 중에 가장 최단경로가 긴 인덱스를 $k$라고 하면 그 $k$는 항상 체인의 시작이나 끝이다.

여기까지 관찰했고 아래 쿼리처럼 날릴 생각을 못하고 구현을 더럽게 들어가서 더럽게 꼬였다.

$k$ 와 다른 $n-1$ 개의 노드들에 대해 query 2를 날린다.

이제 정확히 쿼리를 쓴 횟수는 $2n$이다.

이제 $k$를 체인의 시작이나 끝에 두고 체인을 순회하며 거리가 올바른 것을 넣어준다음, 우리가 채운것은 인덱스에 대한 것이므로 순열을 재구성하려면 역함수를 출력해줘야한다.

배운점

• 어떤 경로가 뒤죽박죽으로 표현될 땐 그 순서들을 모아둔다음 쉽게 처리해주자 => 여러 달팽이 순서나 배열 돌리기 문제들에서 흔한 테크닉
• Interactive 문제는 입출력이 어떻게 되는지 좀더 꼼꼼히 읽자
• 순열을 다룸에 있어 이게 인덱스를 다루는 건지 순열의 값을 다루는 건지 헷갈리기 쉬우므로 유의하자.
• 1시간 이상 안풀리면 아이디어를 잡았더라도 그만 쳐풀고 에디토리얼을 좀 보자

struct _random {  
   mt19937 gen;  
   _random() : gen((unsigned) chrono::steady_clock::now().time_since_epoch().count()) {}  
   template<class T = int>  
   T nextInt(T l = 0, T r = 32767) { return uniform_int_distribution<T>(l, r)(gen); }  
   double nextDouble(double l = 0, double r = 1) { return uniform_real_distribution<double>(l, r)(gen); }  
} rd;  
  
int n, query_cnt;  
vvi edges;  
vi a;  
  
void init() {  
   query_cnt = 0;  
   cin >> n;  
#ifdef LOCAL  
   edges = vvi(n + 1);  
   a = vi(n + 1);  
   for (int i = 1; i <= n; i++) cin >> a[i];  
   //iota(all(a), 0);  
   //shuffle(a.begin() + 1, a.end(), rd.gen);  
   //a = {0, 3, 2, 1, 5, 4};  
   debug(a);  
#endif  
}  
  
int query1(int x) {  
   int ret;  
   query_cnt++;  
   cout << "+ " << x << endl;  
   cout.flush();  
#ifdef LOCAL  
   for (int i = 1; i <= n; i++) {  
      if (x - i >= 1 && x - i <= n) {  
         edges[i].pb(x - i);  
         //debug(i, x - i);  
      }  
   }  
   ret = 1;  
#else  
   cin >> ret;  
#endif  
   return ret;  
}  
int dist[1001][1001];  
int query2(int i, int j) {  
   int ret;  
   query_cnt++;  
   cout << "? " << i << ' ' << j << endl;  
   cout.flush();  
#ifdef LOCAL  
   i = a[i], j = a[j];  
   vi dp(n + 1, 1e9);  
   dp[i] = 0;  
   queue<int> q;  
   q.push(i);  
   while (sz(q)) {  
      int cur = q.front();  
      q.pop();  
      for (int to: edges[cur]) if (dp[to] > dp[cur] + 1) dp[to] = dp[cur] + 1, q.push(to);  
   }  
   if (dp[j] == 1e9) ret = -1;  
   else ret = dp[j];  
#else  
   cin >> ret;  
#endif  
   return ret;  
}  
  
void solve() {  
   init();  
  
   assert(n >= 2);  
   query1(n + 1);  
   query1(n);  
   for (int i = 2; i <= n; i++) {  
      int ret = query2(1, i);  
      debug(i, n, ret);  
      dist[1][i] = dist[i][1] = ret;  
   }  
   vi idx(n + 1);  
   iota(all(idx), 0);  
   sort(idx.begin() + 1, idx.end(), [&](int i, int j) {  
      return dist[1][i] > dist[1][j];  
   });  
   int k = idx[1];  
   vi p1(n + 1), p2(n + 1);  
  
   vi order(n + 1);  
   order[n] = n;  
   for (int i = n - 1, p = 0; i >= 1; i--, p ^= 1) {  
      order[i] = p == 0 ? n + 1 - order[i + 1] : n - order[i + 1];  
   }  
  
   for (int i = 1; i <= n; i++) {  
      if (i != k) {  
         int ret = query2(k, i);  
         dist[i][k] = dist[k][i] = ret;  
      }  
   }  
  
   // p[k] 가 처음이나 끝이다.  
  
   //p1[order[1]] = k;  
   p1[k] = order[1];  
   for (int i = 2; i <= n; i++) {  
      for (int j = 1; j <= n; j++) {  
         if (j != k && dist[k][j] == i - 1) {  
            p1[j] = order[i];  
            //p1[order[i]] = j;  
            break;  
         }  
      }  
   }  
   reverse(order.begin() + 1, order.end());  
   //p1[order[1]] = k;  
   p2[k] = order[1];  
   for (int i = 2; i <= n; i++) {  
      for (int j = 1; j <= n; j++) {  
         if (j != k && dist[k][j] == i - 1) {  
            p2[j] = order[i];  
            //p1[order[i]] = j;  
            break;  
         }  
      }  
   }  
  
   cout << "! ";  
   for (int i = 1; i <= n; i++) cout << p1[i] << ' ';  
   for (int i = 1; i <= n; i++) cout << p2[i] << ' ';  
   cout << endl;  
   cout.flush();  
   int r;  
   cin >> r;  
   assert(query_cnt <= n * 2);  
}