Codeforces Round 864 (Div. 2)
A. Li Hua and Maze (800)
$n, m \ge 4$ 임을 관찰한다. 항상 일자로 막아도 최소 $4$개는 필요하다.
그런데 $4$개면 항상 어떤 한 cell을 완전히 감쌀 수 있으므로 두 개중 더 최소로 감싸지는 것의 개수가 정답이다.
B. Li Hua and Pattern (1100)
일단 180도 돌리고 서로 다른 것의 개수를 센다.
그것의 개수를 $k'$ 라 할때, $k' > k$ 면 정답은 불가능하다.
그렇지 않다면 $k-k'$가 짝수라면 아무 cell이나 계속 짝수번 바꾸면 동일하기 때문에 가능하다.
$n$이 홀수면 제일 중앙에 있는 부분을 계속 바꿔도 돼서 $k' \le k$ 기만 하면 가능하고
그렇지 않다면 $2 \mid k-k'$ 여야 가능하다.
C. Li Hua and Chess (1600)
$(1,1)$ 에 쿼리를 날리면 후보군의 어떤 사각형의 반 테두리가 얻어진다.
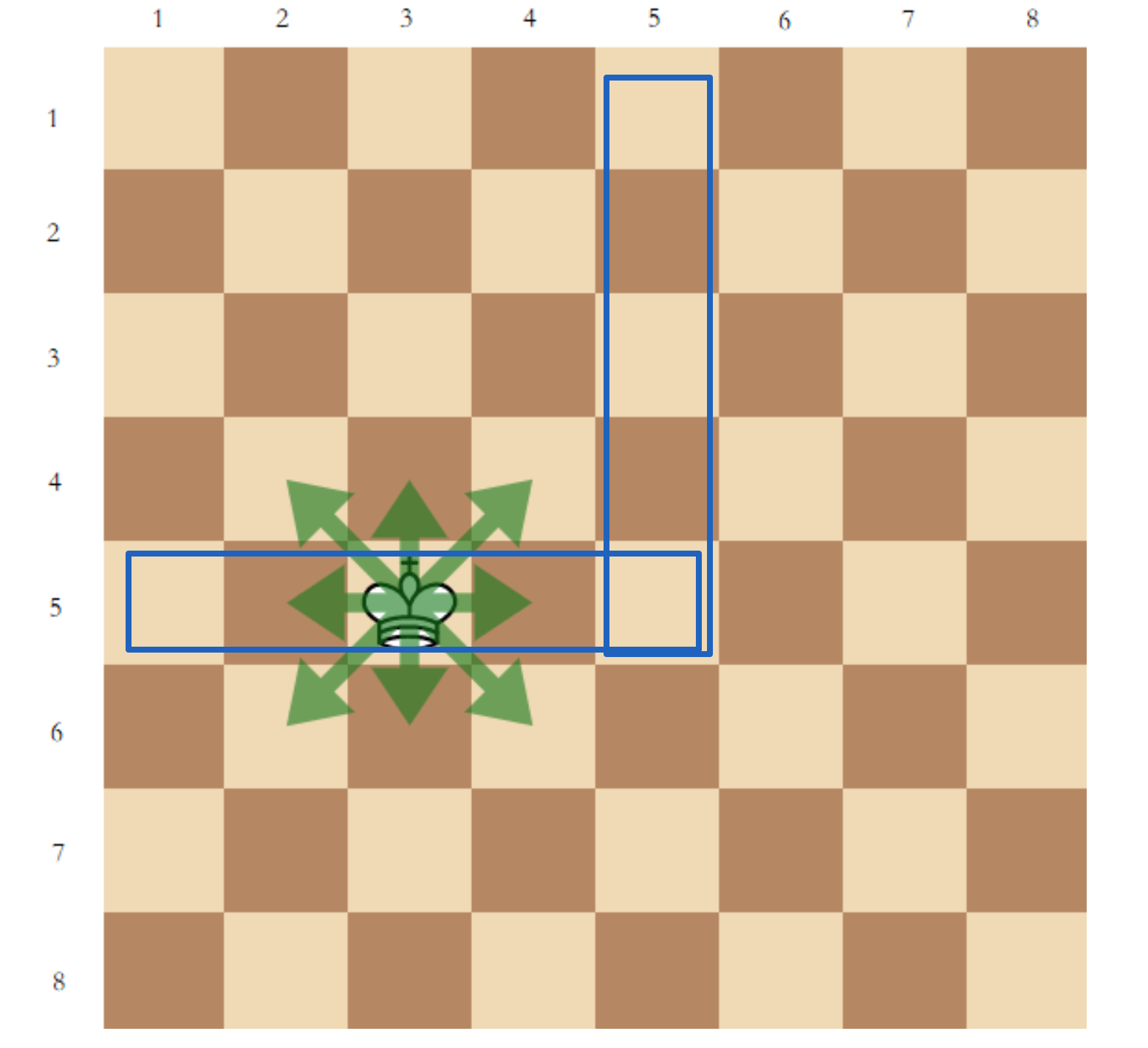
그럼 이제 위에서는 $(5, 5)$ 에 쿼리를 날리면 $(3,5)$나 $(5,3)$ 으로 좁힐 수 있고 나머지 한 번의 쿼리로 그 위치를 찾아낼 수 있다.
만약 $n, m$ 이 제한된다면 나머지 한번의 쿼리를 안 쓰고도 가능하다.
첫 번째 쿼리의 결과가 $a$라면 $(\text{Min}(n, 1+a), \text{Min}(m, 1+a))$ 에 쿼리를 날리면 세로가 짧은 경우 가로가 짧은 경우를 케이스워크로 구해줄 수 있다.
D. Li Hua and Tree (1900)
딱히 설명할 거리가 없는 그냥 트리에서 구현하는 문제이다.
re-rooting비슷하게 배열의 여러가지 값들을 잘 관리하고 간선 관계도 vector 대신 set 같은것을 이용하면 된다.
set에 간선을 저장할 땐 $(\text{서브트리 크기}, i)$ 와 같은 형태로 저장하고 set 의 비교 함수를 서브트리의 크기 내림차순, $i$ 에 대해 오름차순으로 설정하고 관리할 수 있다.
E. Li Hua and Array (2300)
재빠르게 $\phi^k(n)$ 이 어떤 꼴로 나오는지를 본다.
$5,000,000$ 까지 어떤 수도 최대 $23$번이면 $\phi$의 연쇄를 통해 $1$에 도달할 수 있다.
따라서 우린 이걸 트리로 관리할 수 있게 된다.
$1$ 번 쿼리는 DSU나 DP로 자신의 오른쪽에서 가장 먼저 $1$ 이 나오지 않는 수를 계속 관리한다.
$1$번 쿼리는 직접 처리해주면 결국 $O(n \cdot 23)$ 이면 모두 처리가 가능하기 때문에 그냥 처리해준다.
$2$ 번 쿼리는 좀 까다로운데, LCA에 대한 세그먼트 트리와 각 인덱스에 대한 레벨의 세그먼트 트리를 독립적으로 관리하자.
$1$번 쿼리에서 감소할 때 이 두 세그먼트 트리의 값을 잘 변경하고 $[l, r]$ 에서 LCA의 level을 $k$ 라고 한다면
$\displaystyle \sum_{i=l}^{r} level[i]-(r-l+1)k$ 가 정답이 된다.
구현 존나길다.
const int MAX = 5e6;
vector<int> primes, spf(MAX + 1, -1), phi(MAX + 1);
inline ll poww(ll a, ll b, ll mod = -1) {
ll ret = 1;
while (b) {
if (b & 1) {
ret *= a;
if (~mod) ret %= mod;
}
a *= a;
if (~mod) a %= mod;
b >>= 1;
}
return ret;
}
void sieve() {
phi[1] = 1;
for (int i = 2; i <= MAX; i++) {
if (spf[i] == -1) {
primes.pb(i);
spf[i] = i;
phi[i] = i - 1;
}
for (int p: primes) {
if (i * p > MAX) break;
spf[i * p] = p;
if (!(i % p)) {
phi[i * p] = phi[i] * p;
break;
}
phi[i * p] = phi[i] * phi[p];
}
}
}
inline bool prime(int x) {
if (x < 2 || x > MAX) return 0;
if (sz(primes)) return spf[x] == x;
for (int i = 2; i * i <= x; i++) if (!(x % i))return 0;
return 1;
}
inline vector<pi> factorize(int x) {
vector<pi> ret;
while (x > 1) {
int p = spf[x], c = 0;
while (spf[x] == p)c++, x /= spf[x];
ret.pb({p, c});
}
return ret;
}
vi a;
int level[MAX + 1];
void pre_calc() {
int L = 0;
for (int i = 2; i <= MAX; i++) {
level[i] = level[phi[i]] + 1;
maxa(L, level[i]);
}
}
int lca(int u, int v) {
for (; u ^ v; u = phi[u]) if (level[u] < level[v]) swap(u, v);
return u;
};
// region FENWICK
template<class T>
struct fenwick {
int n;
vector<T> tree;
fenwick(int n) : n(n) { tree.resize(n + 1); }
T sum(int i) {
T ret = 0;
for (; i; i -= i & -i) ret += tree[i];
return ret;
}
void update(int i, T x) { for (i++; i <= n; i += i & -i) tree[i] += x; }
T query(int l, int r) { return l > r ? 0 : sum(r + 1) - sum(l); }
};
template<class T>
struct fenwick_point {
fenwick<T> f;
fenwick_point(int n) : f(fenwick<T>(n + 1)) {}
void update(int l, int r, T x) { f.update(l, x), f.update(r + 1, -x); }
T query(int i) { return f.query(0, i); }
};
template<class T>
struct fenwick_range {
fenwick<T> d, c;
fenwick_range(int n) : d(fenwick<T>(n + 1)), c(fenwick<T>(n + 1)) {}
void update(int l, int r, T x) {
d.update(l, x), d.update(r + 1, -x), c.update(l, (1 - l) * x), c.update(r + 1, r * x);
}
T query(int l, int r) {
l--;
return d.query(0, r) * r + c.query(0, r) - (l >= 0 ? d.query(0, l) * l + c.query(0, l) : 0);
}
};
// endregion
const int inf = 1e9;
template<class T>
struct seg_tree_lca {
private:
struct node {
T min, min_level;
node(T v) : min(v), min_level(level[min]) {}
node(T v, T min_level) : min(v), min_level(min_level) {}
};
const node identity{inf, inf};
int N;
vector<node> tree;
node merge(node l, node r) {
int L = l.min == inf ? r.min : r.min == inf ? l.min : lca(l.min, r.min);
node ret = {L, level[L]};
return ret;
}
void update(int n, int nl, int nr, int i, T v) {
if (nl > i || nr < i) return;
if (nl == nr) {
tree[n] = node(v); // diff or assign?
return;
}
int m = (nl + nr) >> 1;
update(n * 2, nl, m, i, v);
update(n * 2 + 1, m + 1, nr, i, v);
tree[n] = merge(tree[n * 2], tree[n * 2 + 1]);
}
node query(int n, int nl, int nr, int l, int r) {
if (nl > r || nr < l) return identity;
if (nl >= l && nr <= r) return tree[n];
int m = (nl + nr) >> 1;
return merge(query(n * 2, nl, m, l, r), query(n * 2 + 1, m + 1, nr, l, r));
}
public:
seg_tree_lca(int N) : N(N) {
int tree_size = 1 << ((int) ceil(log2(N)) + 1);
tree = vector<node>(tree_size, identity);
}
void update(int i, T v) { update(1, 0, N - 1, i, v); }
node query(int l, int r) { return query(1, 0, N - 1, l, r); };
};
struct DSU {
vector<int> p, r;
DSU(int n) : p(n, -1), r(n, n) {
for (int i = n - 2; i >= 0; i--)
r[i] = a[i + 1] == 1 ? r[i + 1] : i + 1;
}
int gp(int n) {
if (p[n] < 0) return n;
return p[n] = gp(p[n]);
}
void merge(int a, int b, int to_b = 0) {
a = gp(a), b = gp(b);
if (a == b) return;
if (!to_b && size(a) > size(b)) swap(a, b);
p[b] += p[a];
p[a] = b;
maxa(r[b], r[a]);
}
bool is_merged(int a, int b) { return gp(a) == gp(b); }
int size(int n) { return -p[gp(n)]; }
int right(int n) { return r[gp(n)]; }
};
void solve() {
int n, m;
cin >> n >> m;
a.resize(n);
fv(a);
DSU dsu(n);
fenwick<int> level_fenw(n);
seg_tree_lca<int> seg_lca(n);
for (int i = 0; i < n; i++) {
level_fenw.update(i, level[a[i]]);
seg_lca.update(i, a[i]);
}
debug();
debug(dsu.r);
while (m--) {
int c, l, r;
cin >> c >> l >> r, l--, r--;
if (c == 1) {
int x = l;
while (x <= r) {
int nxt = dsu.right(x);
if (a[x] != 1) {
level_fenw.update(x, -1);
a[x] = phi[a[x]];
seg_lca.update(x, a[x]);
if (a[x] == 1) {
if (x)dsu.merge(x, x - 1);
//if (x < n - 1)dsu.merge(x, x + 1);
}
}
x = nxt;
}
debug(a);
} else {
if (l == r) {
cout << 0 << endl;
continue;
}
int mn_level = seg_lca.query(l, r).min_level;
assert(mn_level >= 0);
int ret = -mn_level * (r - l + 1);
ret += level_fenw.query(l, r);
cout << ret << endl;
// l ~ r 에서 mn_level 이상인 것들의 합
}
}
}


Comments