Codeforces Round 862 (Div. 2) - E. There Should Be a Lot of Maximums (2300)

E. There Should Be a Lot of Maximums

$c_i$ 를 숫자 $i$가 나오는 횟수라고 하자.

모두 $c_i=2$라고 하자.

$i$ 가 큰 것부터 봤을 때, $c_i > 2$ 라면 항상 어떤 간선을 골라도 한 쪽에는 최소 2개가 있어서 어떤 간선을 끊어도 항상 정답이 $i$ 가 될 수 있다.

$c_i=1$ 라면 그것만으로 두개가 될 수 없으므로 정답에 영향을 미치지 않는다.

여기까지 보고 세 가지의 풀이를 보자.

내 풀이

가장 $i$가 큰 것중 먼저 나오는 것을 $x$ 라고 하고 그 두 정점을 $u, v$ 라고 하자.

$\overline{u,v}$ 경로에 있는 간선들을 제외한 간선들은 끊어도 항상 한 쪽에 $u,v$가 있을 것이므로 정답은 $x$ 이다.

그 경로에 있는 정점들의 집합을 순서대로 $\{u,a_1,a_2,\dots,v\}$ 라고 하자.

이제 $x$ 쪽은 모두 봤고 그 다음 작은 수 $y$ 를 고려한다.

$y$ 도 정점이 두개가 있다.

그 두 개의 정점이 트리의 어디에 존재하든 항상 $u,a_1,a_2\dots,v$ 에서 연속된 구간을 남긴다.

그 두 정점이 모두 그 경로 안에 있다면 그 부분만 남고 다른 부분은 정답을 $y$ 로 설정해주고 지워줄 수 있다.

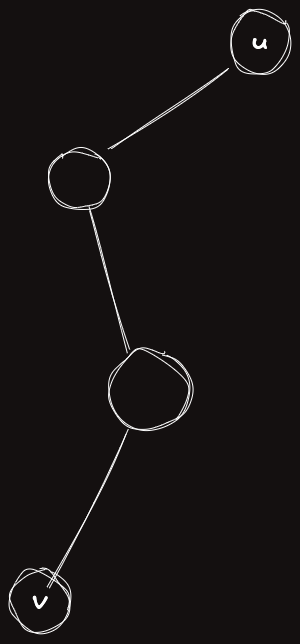
한 정점이 경로 안에 있고 다른 점은 경로 밖에 있거나 모두 경로 밖에 있어도 항상 그렇게 된다는 것을 관찰을 통해 알 수 있다.

따라서 경로의 연속된 정점들을 deque로 관리하며 앞뒤로 지워줄 수 있다.

앞뒤로 지워주는 조건은 어떤 두 정점 $u', v'$ 의 거리의 거리를 $d(u', v')$ 라 할 때, $d(u',v') \neq d(k, u') + d(k, v')$ 인 경우엔 지워주면 된다.

$d(u',v') = d(k, u') + d(k, v')$ 라면 경로 안의 정점 $k$ 가 $\overline{u', v'}$ 에 존재한다는 의미이기 때문이다.

경로의 길이는 LCA같은걸로 전처리해서 구해두고 이렇게 투포인터로 앞뒤로 빼주며 정답을 갱신해줄 수 있다.

이 풀이는 세 가지 풀이중 아마 가장 길고 어려운 풀이일 것이다.

struct LCA {
   int N, LOG = 0;
   vvi p, edges;
   vi level;
   LCA(int N) : N(N), edges(N), level(N, -1) {
      for (; (1 << LOG) <= N; LOG++);
      p = vvi(N, vi(LOG, -1));
   }
   void add_edge(int i, int j) { edges[i].pb(j); }
   void dfs(int cur, int l) {
      level[cur] = l;
      for (int to: edges[cur])
         if (level[to] == -1) p[to][0] = cur, dfs(to, l + 1);
   }
   void build(int root = 0) {
      dfs(root, 0);
      for (int k = 1; k < LOG; k++)
         for (int i = 0; i < N; i++)
            if (~p[i][k - 1]) p[i][k] = p[p[i][k - 1]][k - 1];
   }
   int find(int i, int j) {
      if (level[i] < level[j]) swap(i, j);
      for (int diff = level[i] - level[j], k = 0; diff; diff >>= 1, k++)
         if (diff & 1) i = p[i][k];
      if (i == j) return i;
      for (int k = LOG - 1; k >= 0; k--)
         if (p[i][k] != p[j][k])
            i = p[i][k], j = p[j][k];
      return p[i][0];
   }
   int dist(int i, int j) {
      int l = find(i, j);
      return level[i] + level[j] - 2 * level[l];
   }
};
void solve() {
   int n;
   cin >> n;
   LCA lca(n);
   vector<vector<pi>> edges(n);
   map<pi, int> edge_idx;
   map<int, vi> idx;
   for (int i = 0; i < n - 1; i++) {
      int u, v;
      cin >> u >> v, u--, v--;
      edges[u].pb({v, i});
      edges[v].pb({u, i});
      lca.add_edge(u, v);
      lca.add_edge(v, u);
      edge_idx[mp(u, v)] = edge_idx[mp(v, u)] = i;
   }
   lca.build();
   map<int, int> cnt;
   vi ans(n - 1), val(n);
   fv(val);
   for (int i = 0; i < n; i++)
      idx[val[i]].pb(i);
   for (int i: val) cnt[i]++;
 
   for (auto it = cnt.rbegin(); it != cnt.rend();) {
      int x = it->fi;
      if (it->se >= 3) {
         for (int i = 0; i < n - 1; i++) {
            cout << it->fi << endl;
         }
         return;
      }
      if (it->se == 1) {
         it++;
         continue;
      }
      int u = -1, v = -1;
      for (int i = 0; i < n; i++) {
         if (val[i] == it->fi) {
            if (u == -1) u = i;
            else v = i;
         }
      }
 
      int P = lca.find(u, v);
      deque<int> line, line2;
      int cur = u;
      while (cur != P) {
         line.pb(cur);
         cur = lca.p[cur][0];
      }
      line.pb(P);
      cur = v;
      while (cur != P) {
         line2.pb(cur);
         cur = lca.p[cur][0];
      }
      reverse(all(line2));
      for (int i: line2) line.pb(i);
      for (int i = 1; i < sz(line); i++) {
         int u = line[i - 1], v = line[i];
         ans[edge_idx[mp(u, v)]] = -1;
      }
      for (int i = 0; i < n - 1; i++) if (ans[i] != -1) ans[i] = it->fi;
 
      while (sz(line)) {
         it++;
         if (it == cnt.rend()) break;
         int x = it->fi;
         if (it->se == 1) continue;
         if (it->se >= 3) {
            for (int i = 0; i < n - 1; i++) if (ans[i] == -1) ans[i] = x;
            line = {};
            break;
         }
         int A = idx[x][0], B = idx[x][1];
         int d = lca.dist(A, B);
         while (sz(line) > 1 && d != lca.dist(line[0], A) + lca.dist(line[0], B)) {
            ans[edge_idx[mp(line[0], line[1])]] = x;
            line.pop_front();
         }
         while (sz(line) > 1 && d != lca.dist(line.back(), A) + lca.dist(line.back(), B)) {
            ans[edge_idx[mp(line[sz(line) - 1], line[sz(line) - 2])]] = x;
            line.pop_back();
         }
         if (sz(line) == 1) {
            for (int i = 0; i < n - 1; i++) if (ans[i] == -1) ans[i] = x;
            line = {};
            break;
         }
      }
      for (int i = 0; i < n - 1; i++) if (ans[i] == -1) ans[i] = 0;
      break;
   }
   for (int i = 0; i < n - 1; i++) cout << ans[i] << endl;
}

에디토리얼 풀이

내 풀이와 유사한데 트리가 아닌 직선상의 경로는 충분히 map 이나 set 같은걸로 스위핑을 해주며 값을 관리해줄 수 있다는 점을 이용한다.

따라서 $c_i=2$ 인 경우만 고려하면 된다는 관찰은 동일하게 하고 가장 큰 $i$ 를 찾았다면 경로를 DFS로 구성하고 그 일자 경로를 쭉 자료구조로 관리하며 왼쪽 오른쪽에서 직접 문제에서 요구하는 MAD를 구현해서 구해주면 된다.

Sack(DSU on Tree) 풀이

에디토리얼에 이 댓글 을 보고 공부했다.

Sack 이란건 이분이 지은 이름같은데 Small To Large 테크닉을 트리에서 응용해서 사용하는 개념인 것 같다.

이 부분에 대해선 따로 알고리즘 포스팅으로 정리를 해야겠다.