BOJ 27557 - Moo Route
BOJ 27560
USACO Silver의 3번 문제이다.
이 문제의 해답에서 제시하는 아이디어를 먼저 파악해보자.
먼저 방향 전환을 가장 적게하는 횟수는 $\left(\displaystyle \sum_{i = -1}^{N-1} \dfrac{\vert A_i-A_{i+1} \vert}{2}\right) -1$ 이다.
$A_{-1}=A_N=0$ 으로 둔다.
오일러 회로가 존재하려면 항상 나가는 간선의 개수 = 들어오는 간선의 개수여야 하므로 모든 $A_i$는 짝수이다.
또한 $A_i/2$ 만큼 $A_i$에서 왼쪽으로 이동하는 횟수와 오른쪽으로 이동하는 횟수가 같다.
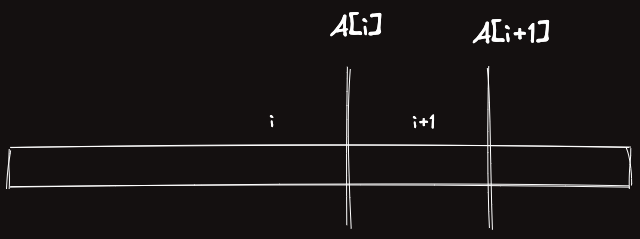
$A_i > A_{i+1}$ 라면 최소 $\dfrac{A_i-A_{i+1}}{2}$ 만큼 방향 전환이 이 생긴다.
$A_i/2$ 번 $i.5$ 에서 왼쪽으로 진행해야 하는데 $LL$ 이 되기위해서는 이전의 $L$이 $i+2 \rightarrow i+1$ 로 가는 $L$이여야 하고, 이는 최대 $A_{i+1}/2$ 번이기 때문에 방향 전환이 생기기 때문이다.
$A_i < A_{i+1}$ 도 유사하게 그렇다.
$i=-1$ 일땐 첫 번째 문자앞에 어떤 문자도 붙지 않기 때문에 총 횟수에 $-1$ 을 해준다.
$\left(\displaystyle \sum_{i = -1}^{N-1} \dfrac{\vert A_i-A_{i+1} \vert}{2}\right) -1$ 만큼 방향전환만 하도록 해를 구성하는 방법이 항상 있기 때문에 이것이 최적이다.
구성하는 방법은 생략한다.
BOJ 27557
$A_i / 2 \ge A_{i+1} / 2$ 라고 하자.
그럼 $i+2 \to i+1$ 로 가는 $L$은 그 다음에 $i \leftarrow i+1$로 가는 $L$ 이 항상 붙어야 한다.
경우의 수에 영향을 미치지 않는다.
더욱 중요하게, $i \to i+1$ 로 가는 $R$은 정확히 $A_{i+1} / 2$ 개의 $R$이 뒤따라 붙고 $A_{i+1}/2$ 개의 $L$이 뒤따라 붙는다.
이 $L$들을 언제 붙일지가 결국 경우의 수를 파생시킬 수 있는 핵심이다.
$A_i / 2 \le A_{i+1}/2$ 인 경우도 유사하다.
한 가지 더 제약은 Bessie가 다시 $x=0$ 으로 돌아오기 위해 고려해야할 것이 있다.
$A_i \ge A_{i+1}$ 인 경우만 $A_{i+1}$ 에서 $L$ 을 $i \rightarrow i+1$ 의 $R$ 뒤에 어디에 붙이냐에 따라 경우의 수가 달라지는데,
마지막 $L$은 항상 마지막에 붙여야 하기 때문에 하나의 칸을 빼줘야한다.
해가 올바름에 대한 증명
이러한 경우의 수를 독립적으로 세도 유일한 해를 만든다는 것을 보장할 수 있다.
이 해가 올바른지에 대해서 애디토리얼에서 증명한다.
$0 \leftarrow 1$ 로 가는 마지막 $L$이 진행되었을 때 경로가 만들어졌다고 가정하자.
이전까지의 그러한 $L$은 모두 $0 \to 1$이 그 다음 붙는다.
우린 모든 $i$마다 $A_i/2$개의 $L,R$ 이 모두 사용되었는지 살펴본다.
$L, R$의 개수는 같으므로 경로에서 $A_i / 2$ 개의 $i \rightarrow i+1$ 이 나타났는지 확인하는 것으로 이를 보인다.
$L_0$이 가정에 의해 참이다.
귀납적으로 $A_i/2$개의 $i \leftarrow i+1$ 이 현재 경로에 나타나있다고 하자.
만약 $A_i \ge A_{i+1}$ 라면 $\dfrac{A_i-A_{i-1}}{2}$개의 $i \leftarrow i+1$이 $i \to i+1$ 앞에 있어야 한다. 또한 개중 $A_{i+1}/2$ 개는 $i + 1 \leftarrow i+2$ 보다 먼저 나타나야 한다.
따라서 모든 $A_i / 2$ 개의 $i \leftarrow i+1$이 현재 경로에 나타나려면 $A_i \ge A_{i+1}$ 이기 때문에 모든 $A_{i+1}/2$개의 $i+1 \leftarrow i+2$ 도 경로에 나타나야 한다.
반대로 $A_i \le A_{i+1}$이라면 마지막 $i+1 \leftarrow i+2$ 는 뒤이어 곧바로 $i \leftarrow i+1$ 이 따라붙기 때문에 모든 $i+1 \leftarrow i+2$ 이 나타나야 $i \leftarrow i+1$ 도 모두 나타나있음이 타당해진다. $\square$
정답을 구하는 법
$1,2$ 번을 참고하면 다음과 같다.
Comments