BOJ 24974 - Apple Catching

BOJ 24974 - Apple Catching

에디토리얼을 봤지만 교육적이고 좋은 문제라고 생각한다.

우선, 뭔가 $t$에 대해 정렬하고 스위핑을 함이 자명한데, 이걸 기존의 좌표계에서 생각하면

어떤 사과가 $t$초에 어떤 소와 만날 수 있는지를 판단할 때, 시간에 따라 소가 움직일 수 있는 구간의 길이가 가변적이기 때문에 관리하기가 불가능하다.

좌표계를 $45\degree$로 회전시킨다 생각하자.

이는 $\begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}$ 로 회전시킨다는 것과 동일한데, $\sin \dfrac{\pi}{4}=\cos \dfrac{\pi}{4}=\dfrac{\sqrt{ 2 }}{2}$ 이기 때문에 이런 상수를 없다고 가정하면 단순히

$x'=x-t,~t'=x+t$ 로 재정의해서 좌표계를 회전시킬 수 있다.

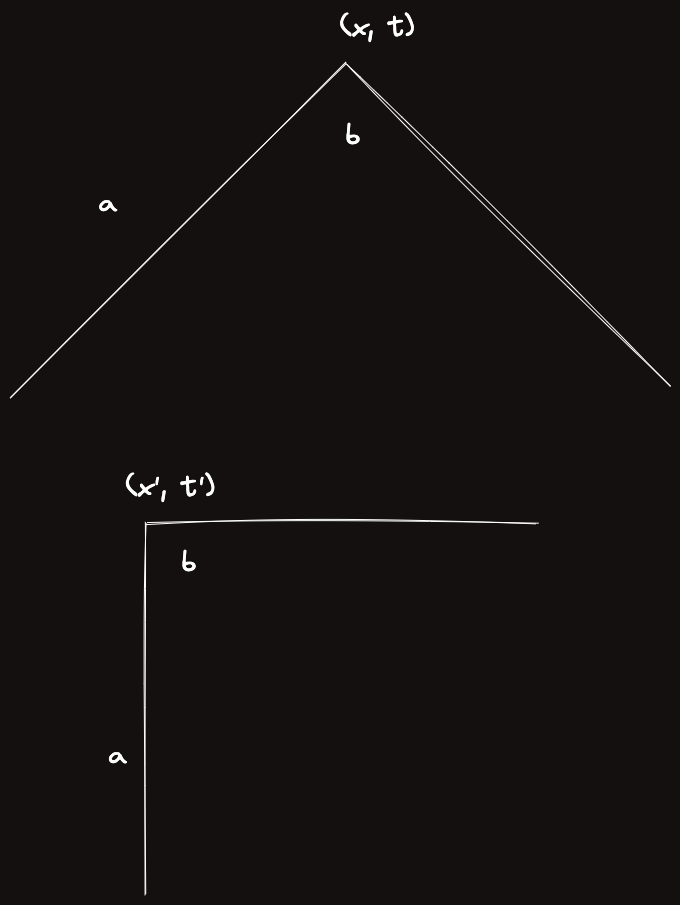
이제 $t'$ 들에 대해 스위핑하며 BBST에 소들의 $x'$ 를 기준으로 정렬하여 그리디하게 뽑을 수 있는 소들 중 가장 왼쪽 소부터 뽑아가며 줄여주는게 최적이다.

struct item {  
   int t, x, n;  
};  
const int inf = 2e9;  
void solve() {  
   int n;  
   cin >> n;  
   vector<item> cow, apple;  
   for (int i = 0, q, t, x, m; i < n; i++) {  
      cin >> q >> t >> x >> m;  
  
      int x2 = x - t;  
      int t2 = x + t;  
  
      if (q == 1) cow.pb({t2, x2, m});  
      else apple.pb({t2, x2, m});  
   }  
   sort(all(cow), [&](auto &a, auto &b) { return a.t < b.t; });  
   sort(all(apple), [&](auto &a, auto &b) { return a.t < b.t; });  
  
   auto cmp = [&](const item &a, const item &b) -> bool {  
      if (a.x != b.x) return a.x < b.x;  
      return a.t < b.t;  
   };  
   set<item, decltype(cmp)> cow_set(cmp);  
  
   int A = sz(apple), C = sz(cow);  
  
   int ans = 0;  
   for (int i = 0, j = 0; i < A; i++) {  
      item a = apple[i];  
      while (j < C && cow[j].t <= a.t) cow_set.insert(cow[j++]);  
      while (sz(cow_set) && a.n > 0 && cow_set.rbegin()->x >= a.x) {  
         item dummy = {inf, a.x - 1, 0};  
         item it = *cow_set.upper_bound(dummy);  
         cow_set.erase(it);  
  
         int add = min(it.n, a.n);  
         ans += add;  
         a.n -= add;  
         it.n -= add;  
         if (it.n > 0) cow_set.insert(it);  
      }  
   }  
   cout << ans;  
  
}