BOJ 23836 - 어떤 우유의 배달목록 (Hard)
BOJ 23836 - 어떤 우유의 배달목록 (Hard)
트리에 등차수열을 끼얹는 연산을 해야되는데,
우선 트리가 아닌 1차원 배열이라면 어떻게 구현할 수 있을지 생각해보자.
이건 BOJ 17353 이 문제다.
에 1부터 시작하고 로 끝나는 등차수열을 더한다.
일단 구간에 1씩 더해주고 에 을 더해준다.
그러면 은 에 이 더해진 값을 얻어올 수 있다.
이걸 트리에 그대로 적용시켜보자.
HLD를 이용하면 는 여러개의 간선 체인(그룹)으로 나뉜다.
이를 라고 하자.
의 경로에서 와 사이에 있는 그룹 에는 이 연산을 거꾸로 해주어야 한다.
그룹 가장 위 노드 에서 까지의 노드의 개수가 개라면,
와 같이 값이 각각 더해져야 한다. 이를 minus path 라고 하자.
이제 그룹이 를 지났다고 한다면, 배열에서 하던거랑 똑같이 씩 더해주고 에 값을 빼주면 된다.
이를 plus path라 하자.
주의할건, 계속 만 더해주는게 아니라 이전 그룹의 개수를 고려해주어야 하기 때문에, 누적으로 합을 업데이트 하면서 이번에 들어갈 가 어떤건지 결정해야 한다.
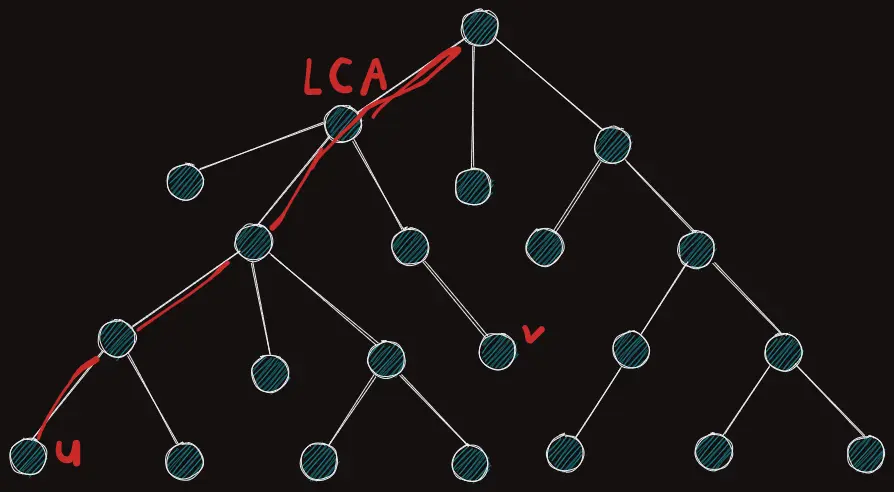
빨간색이 트리에서 무거운 간선이라고 하자.
그럼 head[u] 와 head[v] 가 같지 않을 때 까지 u와 v 를 위로 올려보내면 저 상황에선 v 가 먼저 LCA에 도착한다.
이 문제에선 u와 v 를 swap 하면서 트리를 이동하는것을 지양하는것이 좋다.
순서가 중요하기 때문이다.
그래서 대략적으로 update 함수만 좀 보자면,
void update_path(int a, int b) {
vector<pi> minus_path, plus_path;
while (head[a] ^ head[b]) {
if (depth[head[a]] > depth[head[b]]) {
minus_path.pb({in[head[a]], in[a]});
a = par[head[a]];
} else {
plus_path.pb({in[head[b]], in[b]});
b = par[head[b]];
}
}
if (depth[a] < depth[b]) {
plus_path.pb({in[a], in[b]});
} else {
minus_path.pb({in[b], in[a]});
}
reverse(all(plus_path));
int next_k = 0;
for (auto&[l, r]: minus_path) {
int len = r - l + 1;
next_k += r - l + 1;
seg.update(l, r, -1);
seg.update(l, l, next_k);
seg.update(r + 1, r + 1, -next_k + len);
}
for (auto&[l, r]: plus_path) {
int len = r - l + 1;
seg.update(l, r, 1);
seg.update(l, l, next_k - 1);
seg.update(r + 1, r + 1, -(next_k - 1) - (len));
next_k += len;
}
}
처럼 구현했더니 맞았다.



Comments