BOJ 23569 - Friendship Graphs

BOJ 23569 - Friendship Graphs

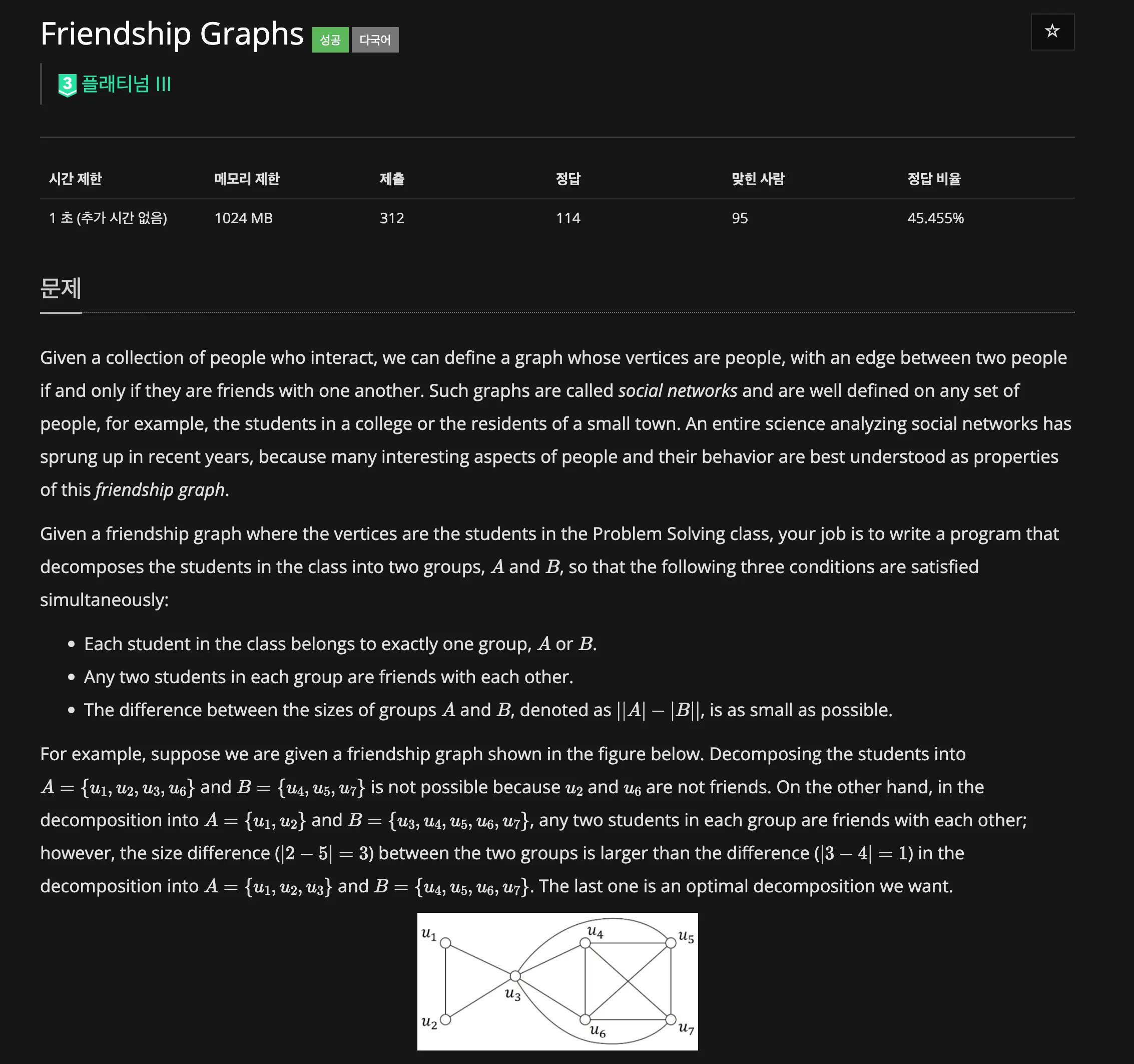
문제를 잘 살펴보자.

정답이 없는 경우를 어떻게 알 수 있을까 생각하다보면 문제가 풀린다.

$M$개의 간선 말고 거기에 포함되지 않은 $\dfrac {N(N+1)}2-M$ 개의 간선을 생각해본다.

그것들로 그래프를 만들어서 $wlog.$ 각 컴포넌트가 Bipartite Graph가 되는지 판별한다. $O(N)$ 이 걸린다.

그렇지 못하다면 정답이 될 수 없다.

이제 각 컴포넌트별로 이분 그래프로 나뉘어진 두 정점들의 크기를 $c_1, c_2$ 라고 하자.

$\lvert c_1-c_2 \rvert$ 를 모두 모아서 Knapsack 을 돌린다. $O(N^2)$ 이 걸린다.

대략 $-N \sim N$의 숫자 들 중 $\lvert c_1-c_2 \rvert$ 를 각각 더하거나 빼서 $0$과 가장 근접하게 나오는 숫자의 절댓값이 정답이다.

참고로 이런식으로 Knapsack을 돌릴 때 std::bitset은 개꿀이므로 알아두도록 하자.

void solve() {  
   int n, m;  
   cin >> n >> m;  
   vvi g(n, vi(n));  
   while (m--) {  
      int u, v;  
      cin >> u >> v, u--, v--;  
      g[u][v] = g[v][u] = 1;  
   }  
   vvi edges(n);  
   for (int i = 0; i < n; i++) {  
      for (int j = i + 1; j < n; j++) {  
         if (g[i][j] == 0) {  
            edges[i].pb(j);  
            edges[j].pb(i);  
         }  
      }  
   }  
   vi vis(n, -1);  
   vi diff;  
   for (int i = 0; i < n; i++) {  
      if (vis[i] != -1)continue;  
      vi cnt(2);  
      function<void(int, int)> fn = [&](int cur, int color) -> void {  
         vis[cur] = color;  
         cnt[color]++;  
         for (int to: edges[cur]) {  
            if (vis[to] == -1) {  
               fn(to, color ^ 1);  
            } else {  
               if (vis[to] == color) {  
                  cout << -1;  
                  exit(0);  
               }  
            }  
         }  
      };  
      fn(i, 0);  
      diff.pb(abs(cnt[0] - cnt[1]));  
   }  
   int D = sz(diff);  
   bitset<2048> dp;  
   dp[1024] = 1;  
   for (int i = 0; i < D; i++) {  
      dp = dp << diff[i] | dp >> diff[i];  
   }  
   for (int i = 0;; i++) {  
      if (dp[1024 - i] || dp[1024 + i]) {  
         cout << i;  
         return;  
      }  
   }  
}