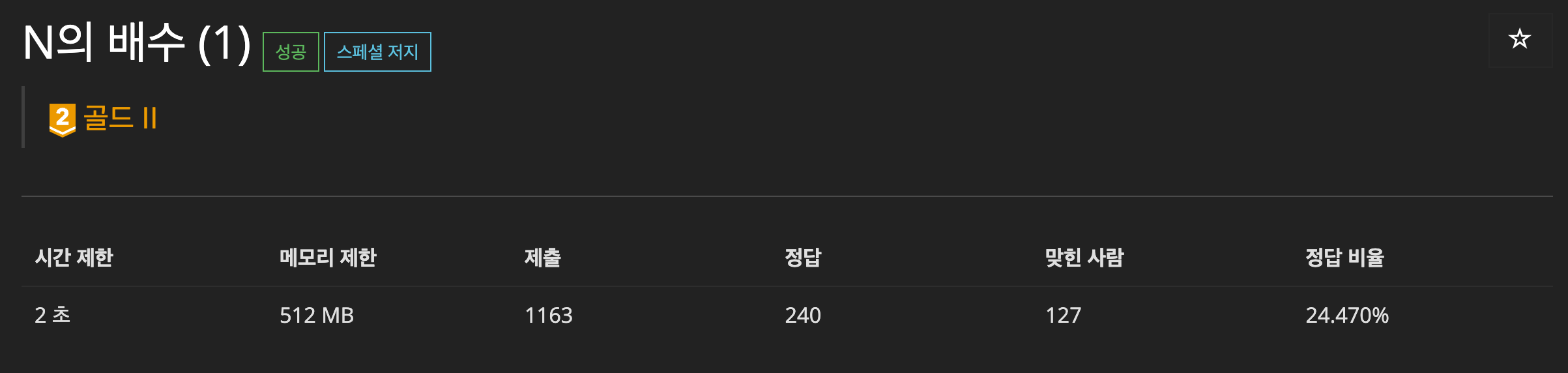
BOJ 18790 - N의 배수 (1)

BOJ 18790 - N의 배수 (1)

$DP$임은 쉽게 알 수 있지만 $O(n^3)$ 으로 돌리고 공간복잡도는 $O(n^2)$ 를 써야해서 반복문 DP가 강제된다.

또한, 상수컷팅을 잘 해줘야 한다.

역추적도 어렵다고 생각한다.

이 문제는 $(4)$ 까지 존재하며 이상한 수학 정리를 쓰면 그걸 증명해서 어떻게 풀 수 있다.

이 문제의 질문 게시판에 솔루션이 있다.

// i 를 j 개를 써서 만들 수 있는가?
bitset<501> dp[501];
int path[501][501];
void solve() {
   memset(path, -1, sizeof path);
   int n;
   cin >> n;
   vi a(n * 2 - 1);
   fv(a);
   dp[0][0] = 1;

   for (int i = 0; i < n * 2 - 1; i++) {
      vector<pi> added;
      for (int j = 0; j < n; j++) {
         for (int u = 1; u <= min(n, i + 1); u++) {
            if (dp[j][u] == 0 && dp[md(n, j - a[i])][u - 1]) {
               added.pb({j, u});
            }
         }
      }
      for (auto &[x, y]: added) {
         dp[x][y] = 1;
         path[x][y] = i;
      }
   }

   if (!dp[0][n]) {
      cout << -1;
      return;
   }

   int remain = n, cur = path[0][n];
   vi ans;
   ans.pb(a[cur]);
   remain--;
   int m = md(n, -a[cur]);
   cur--;
   while (remain) {
      cur = path[m][remain];
      ans.pb(a[cur]);
      m = md(n, m - a[cur]);
      cur--;
      remain--;
   }
   for (int i: ans) cout << i << ' ';
}