BOJ 17454 - 갓
힘들었던 수학문제이다.
만약 $HD > HS$나 $SD > SH$ 라고 하자. 그럼 항상 가능하다.
세 번의 투표들에서 계수를 각각 $x,y,z$ 라고 하자.
$x=1$ 여야 한다. $H,S$ 에게 가능한 적은 표를 주어야 하기 때문이다.
$D$가 $H$를 이겨야 한다고 해보자. 각각 받은 투표수를 $f(D), f(H), f(S)$라 하자.
$f(D)=y \cdot HD + z \cdot SD$ 이고
$f(H)=DH+z \cdot SH$ 이다.
$f(D) > f(H)$ 여야 하므로
$$
\begin{aligned}
y \cdot HD + z \cdot SD > DH + z \cdot SH \\
HD \cdot y>z(SH-SD) + DH
\end{aligned}
$$
이 반평면은 $(y,z)$ 좌표계를 따지면 $\left(\dfrac{DH}{SD-SH}, 0\right)$ 를 지나고 다음과 같이 그려진다.
기울기는 아래처럼 항상 그려지지 않는다.
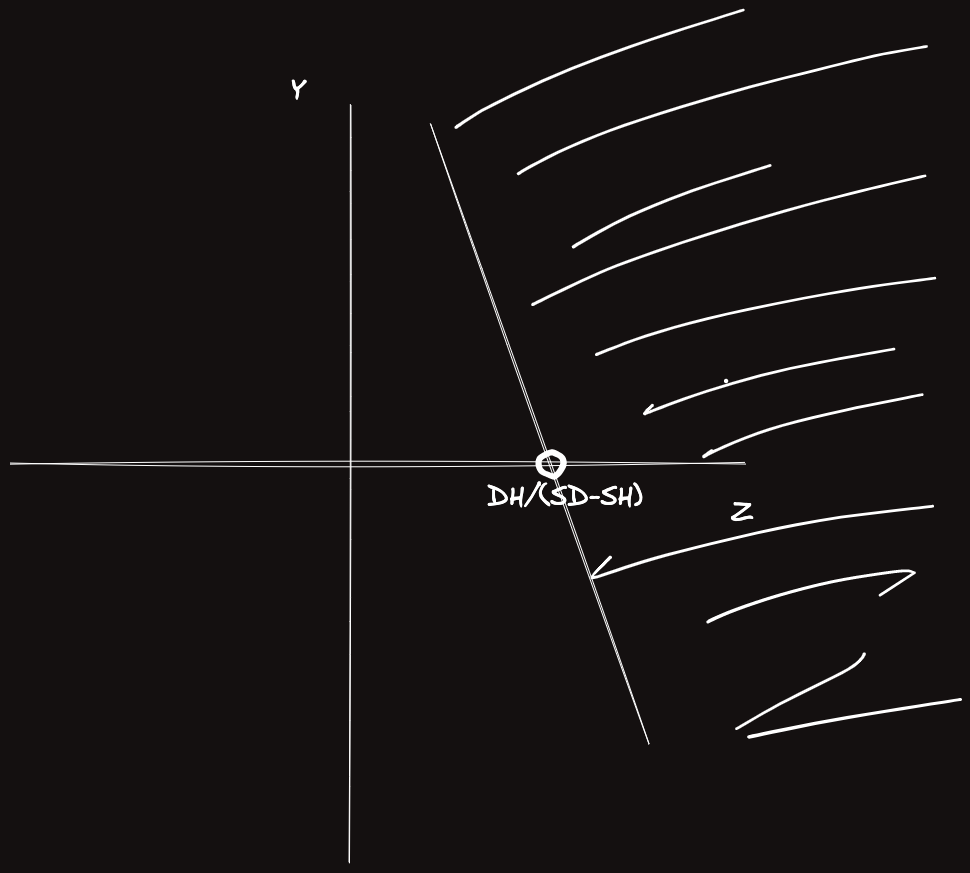
마찬가지로 $f(D) > f(S)$ 가 되는 식을 구하면 어떠한 반평면이 나오고 결국 정답은 겹치는 반평면 좌표 $(z,y)$ 가 있는지에 대한 문제로 환원된다.
공식 해설 링크를 참고해서 풀어보자!
참고로 나는 이 문제를 37틀했다.
Comments