BOJ 16884 - 나이트 게임
이 홀수라면 선공이 이긴다.
일 땐 자명하다.
- 빨간색으로 된
7X7격자가 있다고 할 때, 가장 중앙에 나이트를 둔다.
- 빨간색 체크표시는 둔 곳이다
- 파란색 X 표시는 더 이상 둘 수 없는 곳이다.
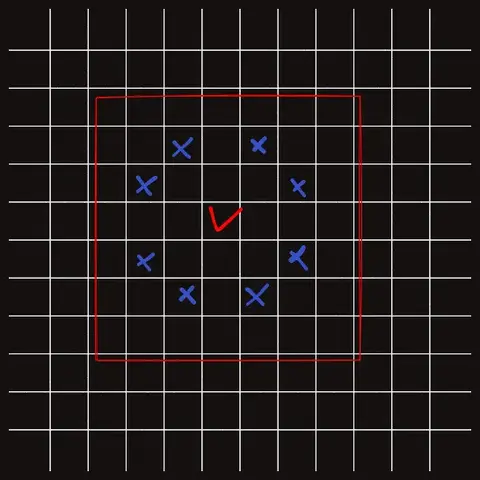
- 상대방이 아무데나 둔다고 해보자.
- 보라색은 상대방이 둔 곳이다
- 주황색 X 표시는 더 이상 둘 수 없는 곳이다.
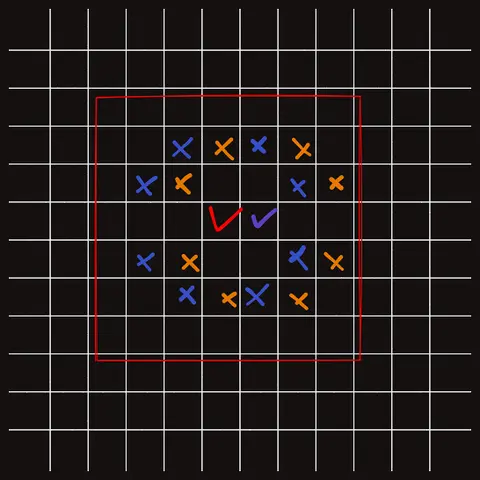
- 상대방이 둔 곳과 중심점과 대칭되는 곳에 수를 둔다
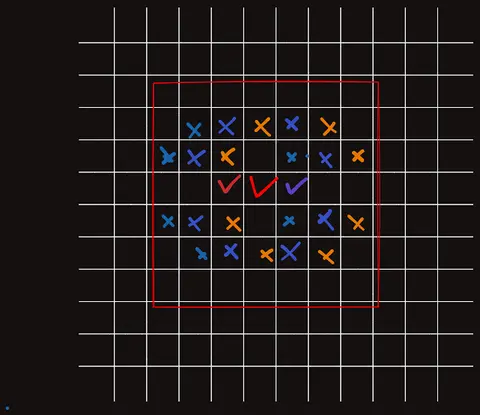
필승법Permalink
항상 상대방이 둔 곳과 중심점과 대칭되는 곳에 수를 둘 수 있기 때문에 N이 홀수인 경우, 선공이 중앙에 두면 승리한다.반대로 짝수인 경우엔 중앙에 둘 수 없으므로 상대방이 계속해서 내가 둔 곳과 대칭점에 나이트를 두면 후공이 승리한다.
증명Permalink
일반성을 잃지 않고 N 이 홀수여서 선공이 중앙에 둔 후부터 상대방이 n 번째에 둔 수를 P_n 이라 하고, 그곳과 대칭되는 위치를 Q_n 이라 하자.
그리고 선공은 후공이 P_n 을 두면 항상 Q_n 을 둔다고 하자.나이트의 이동 경로상 P_1 이 Q_1 을 못 두게 할 수 없으므로 n=1 일 때 성립한다.
따라서 상대방이 P_k 를 착수했을 때 Q_k 를 못 두는 상황은 P_u(u<k) 혹은 Q_u 가 Q_k 를 못 두게 만든 상황이다.
못 두게 되었다는 것은 (1) 그 자리에 이미 수를 두었거나 (2) 다른 자리에 수를 두어 그 자리를 못쓰게 만들었거나 두 상황이다.
- (1)
Q_k에 이미 착수가 되어있다는 것은P_i<=>Q_i의 정의에 모순이다. - (2)
Q_k가 다른 수에 의해 못쓰게 만들어졌다는 것은P_k를 둘 수 있었다는 것에 모순이다.
따라서 Q_k 는 항상 둘 수 있으며 체스판의 착수할 수 있는 칸은 한 수마다 최소 1 씩 감소하기 때문에 게임은 유한한 수 안에 종료되어 선공이 승리한다.



Comments