BOJ 15588 - Stamp Painting

BOJ 15588 - Stamp Painting

새벽에 뭐풀지 하다가 첫 줄에 Bessie 있는거 보고 USACO여서 약간 무서웠는데 결과적으로 퀄리티 있는 좋은 문제였다.

모듈러때문에 식을 다구해놓고 틀려서 고민할뻔했다.

---

문제 설명

M개의 다른 색을 가진 고무 페인트가 있다.

각 스탬프는 K 너비를 갖는다.

캔버스에 도장을 일정한 순서로 찍어 얼마나 다양한 그림을 그릴 수 있는지 정확히 알고 싶어합니다.

도장을 울타리 밖으로 넘어가게 찍을 수 없고, 정수단위로만 가능하다

도장 찍기를 마쳤을 땐 울타리의 각 칸은 최소 한 번은 색칠이 되어있어야 한다.

두개의 같지만 다른 순서로 만들어진 그림은 같은 것으로 세진다.

풀이 과정

DP임이 쉽게 보인다. 식을 세우는게 어려울것같다.

$dp[i]=$ $i$ 길이까지 칠할 때 경우의 수라고 하자.

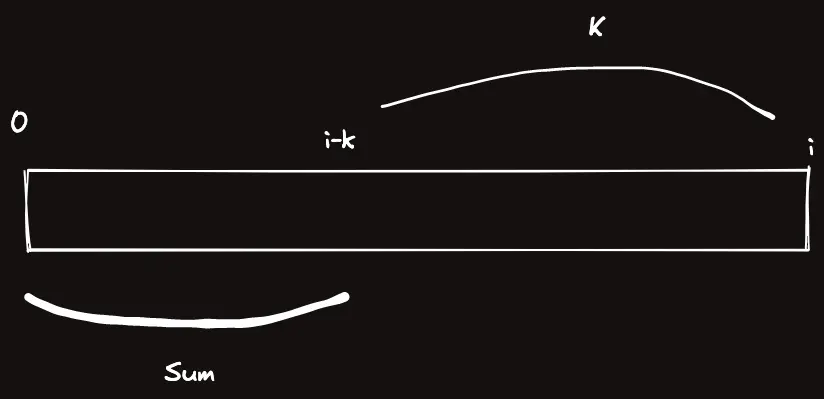
$i$ 를 포함하게 어떤 도장을 칠해보자. 총 $M$개의 색깔수가 나온다.

1- 여길 가장 늦게 칠한다고 해보자.

$[i-k,i]$ 까지 이 색으로 칠해지고 $[0, i-k]$ 까지 경우의 수를 고려하자.

사실 여기는 항상 모든칸을 원하는 색으로 칠할 수 있다. 어차피 $[i-k, i]$ 를 제일 마지막에 칠하기 때문에 이 칸에서의 경우의 수는 $M^{i-k}$ 라고 할 수 있다.

젤 첫 칸부터 원하는 색으로 계속 칠하면서 오른쪽으로 이동하는 것을 생각해보면 된다.

따라서 일단 정답에 $M^{i-k} \cdot M$ 을 더해준다.

2- 여길 가장 늦게 칠하지 않는다고 하자.

겹치게 경우의 수가 세지지 않게 $i-k+1$ 부터 $i-1$ 가 새로운 색의 시작점이 되고 $i$ 가 끝나는 점이 될 때, 바로 왼쪽의 칸과 색이 동일해서는 안된다.

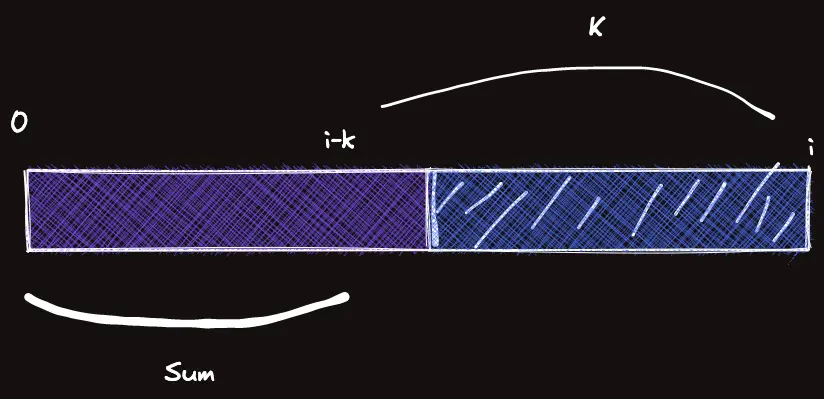
$[i-k+1, i]$ 가 같은 색이고 바로 왼쪽이 다른 색이라고 해보자.

왼쪽에서 경우의 수는 $dp[i-k+1]$ 이고 오른쪽에서 경우의 수(색 수)는 $M$ 개이다.

$dp[i-k+1]\cdot M$을 정답에 더해주면 될까?

$dp[i-k+1]$ 중에 가장 오른쪽 칸이 오른쪽 부분의 색과 겹치는 경우를 제외해줘야 하고, 이는 $dp[i-k+1] \cdot \dfrac 1M$ 개 일 것이므로, 각 색깔마다 $dp[i-k+1] \cdot \dfrac {M-1}M$ 개가 더해지므로,

정답에 $dp[i-k+1] \cdot (M-1)$ 을 더해주는 것이 맞다.

결국,

$$ dp[i]=M^{i-k}\cdot M+\displaystyle \sum_{j=i-k+1}^{i-1}dp[j] \cdot (M-1) $$

이다.

inline ll poww(ll a, ll b) {  
   ll ret = 1;  
   while (b) {  
      if (b & 1) {  
         ret = md(ret * a);  
      }  
      a = md(a * a);  
      b >>= 1;  
   }  
   return ret;  
}  
  
void solve() {  
   int n, m, k;  
   cin >> n >> m >> k;  
   vi dp(n + 1), dp_sum(n + 1);  
   for (int i = 1; i < k; i++) dp[i] = md(dp[i - 1] * m);  
   dp[k] = m;  
   for (int i = 1; i <= k; i++) dp_sum[i] = md(dp_sum[i - 1] + dp[i]);  
   for (int i = k + 1; i <= n; i++) {  
      dp[i] = poww(m, i - k + 1);  
      // dp[i-k+1] ~ dp[i-1]  
      int sum = md(dp_sum[i - 1] - dp_sum[i - k]);  
      dp[i] = md(dp[i] + md(sum * (m - 1)));  
      dp_sum[i] = md(dp[i] + dp_sum[i - 1]);  
   }  
   cout << dp[n];  
}