BOJ 1416 - 팬 서비스

image.png

Solution 1Permalink

O(K⋅9K⋅18K)O(K \cdot 9K \cdot 18K) 정도로 푸는 풀이로 먼저 통과했다.

dp[i][j][k]dp[i][j][k] 를 ii 번 째 수까지 채웠을 때 합이 jj 이고 짝수 - 홀수 = kk 인 경우의 수라고 하자.

포함 배제의 원리로 1번 조건 만족 + 2번 조건 만족 - 1번, 2번 조건 모두 만족을 하는것이 정답이다.

각 jj와 각 kk에 대해 포함되는 모든 값을 미리 더해서 전처리해두면 세가지 모두 O(9⋅18⋅K2)O(9 \cdot 18 \cdot K^2) 에 구할 수 있다.

공간복잡도를 위해 토글링을 해야한다.

const ll mod = 999983;  
inline ll md(ll x) { return md(mod, x); }  
template<class T>  
inline void mds(T &a, T b) { a = md(a + b); }  
template<class T>  
inline void mdp(T &a, T b) { a = md(a * b); }  
vi in;  
int k;  
// i 번째까지, 총합이 j이고, 짝수 - 홀수가 k인 것의 경우의 수  
int dp[2][455][1000];  
int sum_sum[455];  
int sum_diff[1000];  
const int o = 500;  
void solve() {  
   cin >> k;  
   string s;  
   cin >> s;  
   for (char c: s) in.pb(c - '0');  
   sort(all(in));  
  
   dp[0][0][o] = 1;  
   for (int i = 1; i <= k; i++) {  
      int I = i % 2, J = I ^ 1;  
      memset(dp[I], 0, sizeof dp[I]);  
      for (int d: in) {  
         for (int sum = 0; sum <= 9 * i; sum++) {  
            for (int diff = -i * 9; diff <= i * 9; diff++) {  
               if (sum - d >= 0) {  
                  int nxt = i % 2 == 1 ? diff + d : diff - d;  
                  nxt += o;  
                  if (nxt >= 0 && nxt < 1000)  
                     mds(dp[I][sum][diff + o], dp[J][sum - d][nxt]);  
               }  
            }  
         }  
      }  
   }  
   ll ans_all = 0, ans1 = 0, ans2 = 0;  
  
   for (int sum = 0; sum <= k * 9; sum++) {  
      for (int diff = -k * 9; diff <= k * 9; diff++) {  
         mds(sum_sum[sum], dp[k & 1][sum][diff + o]);  
         mds(sum_diff[diff + o], dp[k & 1][sum][diff + o]);  
      }  
   }  
  
   for (int sum = 0; sum <= k * 9; sum++) {  
      for (int diff = -k * 9; diff <= k * 9; diff++) {  
         mds(ans1, 1ll * dp[k & 1][sum][diff + o] * sum_sum[sum]);  
         mds(ans2, 1ll * dp[k & 1][sum][diff + o] * sum_diff[diff + o]);  
         mds(ans_all, 1ll * dp[k & 1][sum][diff + o] * dp[k & 1][sum][diff + o]);  
      }  
   }  
   cout << md(ans1 + ans2 - ans_all);  
}

Solution 2Permalink

조건을 좀 더 살펴보자.

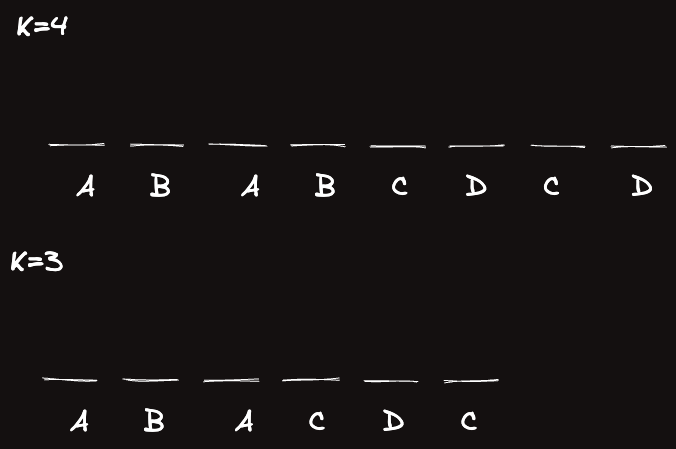
image.png

KK 가 짝수일 때 기준으로,

11번 조건은 ∑A+∑B=∑C+∑D\sum A+\sum B=\sum C + \sum D 를 의미한다.

22번 조건은 ∑A+∑C=∑B+∑D\sum A + \sum C = \sum B + \sum D 를 의미한다.

연립하면 ∑B=∑C\sum B=\sum C 이다. 또한 이로써 ∑A=∑D\sum A = \sum D 도 얻는다.

따라서 dpdp를 그냥 dp[i][j]=idp[i][j]=i 번째 수까지 채웠을 때 합이 jj 가 되는 것이라고 해보자. O(K⋅9K)O(K \cdot 9K) 에 구할 수 있다.

11번 조건의 경우의 수는 그냥 ∑dp[k][j]2\sum dp[k][j]^2 이다.

22번 조건의 경우의 수도 따지고보면 11번 조건의 경우의 수와 다를수 없다.

따라서 구한 값에 ×2\times2 를 해주자.

33번 조건의 경우의 수는 B=C & A=DB=C ~ \& ~ A=D 를 만드는 경우의 수이다.

KK의 기우성에 관계없이 ∑dp[⌊k2⌋][j]2\sum dp[ \left\lfloor \frac{k}{2} \right\rfloor][j]^2 와 ∑dp[⌊k+12⌋][j]2\sum dp[ \left\lfloor \frac{k+1}{2} \right\rfloor][j]^2 를 곱한값을 11번 조건의 경우의 수에 두배한 것에서 빼면 된다.

Tags:

Categories:

Updated:

Comments

You may also enjoy