BOJ 10542 - MAFIJA

BOJ 10542 - MAFIJA

2-Sat 으로 이리저리 해보다가 아닌거같아서 태그는 깠다.

몇가지 Observation을 하며 풀어보려고 한다.

Observaiton 1. 일반성을 잃지않고 연결 그래프이다.

그렇지 않다면 각 나눠진 그래프에서 마피아의 최대값의 합들을 구해주면 된다.

Observation 2. 한 연결 그래프에 싸이클은 1개이다.

싸이클이 두 개 이상 있다고 하자. 그런데 각 정점마다 edge는 항상 1개이므로, 두 싸이클이 연결될 방법이 없어서 모순이다.

싸이클이 없다고 하자. 그러면 $u_1 \to u_2 \to \cdots \to u_k$ 까지 간다는건데, $u_k$ 는 어디로 간선이 이어져야 하는가? $u_{1,\cdots,k-1}$ 까지의 간선들로 갈 순 없고, 자기 자신에 간선을 이을 수 없다는 조건이 있으므로 모순이다.

따라서 싸이클은 항상 1개이다.

증명지렸고

풀이

어떤 연결 그래프엔 싸이클이 1개가 있고, $k$ 개의 싸이클과 연결되지 않은 정점들이 있다.

틀린 풀이 1

대략 그림으로 그려보면 이렇다.

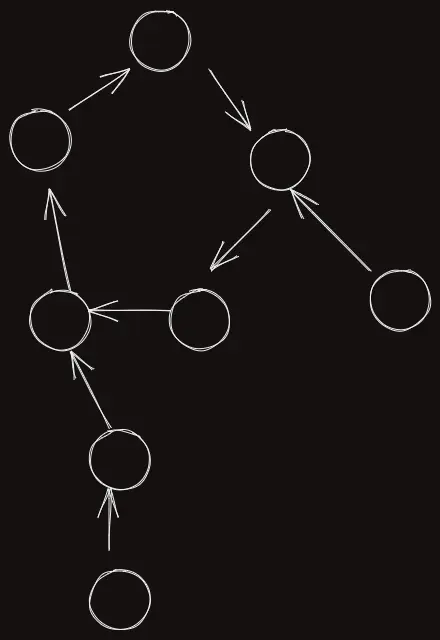
일단 $in_i=0$ 이라면 그냥 마피아 시켜주자. 그러면 이제 마피아가 가리키고 있는 애들은 무조건 시민이다.

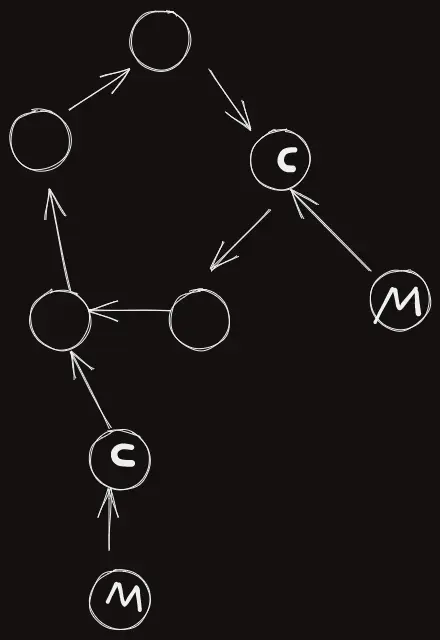
이제 나머지 정점들을 어떻게 처리해야 되냐인데, 순서대로 마피아가 될 수 있는 것부터 그리디하게 넣어주면 되지않을까?

하고 짐작을 해보고 구현을 해보았다. 그랬더니 틀렸다. 망할 Ad-hoc

틀린 풀이 2

싸이클을 먼저 채운다고 하자.

싸이클이 짝수라면 항상 MCMC… 순서로 돌아가므로 싸이클에 마피아와 시민이 차있는 경우의 수가 2가지밖에 안된다.

하지만 싸이클이 홀수라면 MCMC… 하다가 어딘가는 CC가 나와야 한다. 근데, CC가 어디에 나오는게 제일 유리할까?

싸이클에 있는 정점들이 C가 되었을 때 싸이클 외부에 있는 것들에서 마피아가 얼마나 튀어나오는지를 미리 전처리해두었다가 $C_i + C_{i+1}$ 이 최대가 되는 CC 위치를 찾아버리면 어떨까?

아 이것도 아니란걸 깨달았다.

맞는 풀이 1

생각이 났다. $a_i$ 들에 대한 역간선들을 이용해서 싸이클에 있는 어떤 정점을 시작으로 tree dp를 돌리는 것이다.

어떤 정점이 마피아가 될 수 있을 때와 아닐때 서브트리에서의 마피아의 최대 명수를 구해둔다.

이걸 $C_i$ $M_i$ 라고 하자.

$C_i > M_i$ 라면 그 싸이클 내의 정점은 그냥 $C$ 로 두면 된다.

아니라면 $M$ 으로 두고 적절히 $MM$ 끼리 맞닿아 있는 것들을 $MC$ 로 바꿔주니까 그냥 맞아버렸다.

더 정해를 봐야될거같다.

void solve() {  
   int n;  
   cin >> n;  
   vi a(n), in(n);  
   vvi edges(n), edges_rev(n);  
   fv(a);  
   for (int i = 0; i < n; i++) {  
      a[i]--;  
      in[a[i]]++;  
      edges[i].pb(a[i]);  
      edges[a[i]].pb(i);  
      edges_rev[a[i]].pb(i);  
   }  
  
   int mafia = 0;  
   vi vis(n), fin(n), mafia_get_if_c(n), mafia_get_if_m(n), in_cycle(n), prev(n), is_mafia(n);  
   vvi dp(n, vi(2, -1));  
   for (int i = 0; i < n; i++) {  
      if (vis[i]) continue;  
      vi group, cycle_nodes;  
      function<void(int)> fn = [&](int cur) -> void {  
         vis[cur] = 1;  
         group.pb(cur);  
         for (int to: edges[cur]) if (!vis[to]) fn(to);  
      };  
      fn(i);  
  
      for (int i: group)vis[i] = 0;  
      function<void(int, int)> dfs = [&](int cur, int p) -> void {  
         vis[cur] = 1;  
         prev[cur] = p;  
  
         int to = a[cur];  
         if (!fin[to]) {  
            if (!vis[to]) dfs(to, cur);  
            else {  
               // detect cycle  
               prev[to] = cur;  
               int cycle_node = cur;  
               do {  
                  cycle_nodes.pb(cycle_node);  
                  in_cycle[cycle_node] = 1;  
                  cycle_node = a[cycle_node];  
               } while (cycle_node != cur);  
               debug(cycle_nodes);  
            }  
         }  
  
         fin[cur] = 1;  
      };  
      dfs(i, -1);  
  
      function<int(int, int, int)> get_calc = [&](int i, int k, int p) -> int {  
         int &ret = dp[i][k];  
         if (~ret) return ret;  
         int mafia_yes = k, mafia_no = 0;  
         for (int to: edges_rev[i]) {  
            if (to == p) continue;  
            if (k) mafia_yes += get_calc(to, 0, i);  
            mafia_no += get_calc(to, 1, i);  
         }  
         return ret = max(mafia_yes, mafia_no);  
      };  
      for (int j: cycle_nodes) {  
         for (int k: edges_rev[j]) {  
            if (!in_cycle[k]) {  
               mafia_get_if_c[j] += get_calc(k, 1, -1);  
               mafia_get_if_m[j] += get_calc(k, 0, -1);  
            }  
         }  
      }  
      debug(mafia_get_if_c);  
      debug(mafia_get_if_m);  
      int s = -1;  
      for (int j: cycle_nodes) {  
         assert(mafia_get_if_c[j] >= mafia_get_if_m[j]);  
         if (mafia_get_if_c[j] > mafia_get_if_m[j]) {  
            mafia += mafia_get_if_c[j];  
            s = j;  
         } else {  
            is_mafia[j] = 1;  
            mafia++;  
            mafia += mafia_get_if_m[j];  
         }  
      }  
      int cur = s;  
      if (cur == -1) {  
         mafia -= (sz(cycle_nodes) + 1) / 2;  
      } else {  
         do {  
            int nxt = a[cur];  
            if (is_mafia[cur] && is_mafia[nxt]) {  
               is_mafia[nxt] = 0;  
               mafia--;  
               mafia -= mafia_get_if_m[nxt];  
               mafia += mafia_get_if_c[nxt];  
            }  
            cur = a[cur];  
         } while (cur ^ s);  
      }  
      for (int j: group) vis[j] = 1;  
   }  
   cout << mafia;  
}

맞는 풀이 2

아마도 틀린 풀이 1이 올바른 접근법이였던 것 같다.

그냥 무향 그래프에서 인접한 두 노드를 안고를 때 최대로 고를 수 있는 노드의 개수를 구하는 문제로 치환된다.

따라서 leaf 노드들부터 그냥 마피아를 주면서 타고타고 가면서 그리디하게만 선택해주면 되는 문제인 것 같다.

---

간만에 재밌는 그래프 문제였다.