Floyd Tortoise Hare Algorithm - 토끼와 거북이 알고리즘
이 문제를 정의하기에 재밌는 영상이 있어서 미리 보면 좋다.
토끼와 거북이 알고리즘(플로이드 알고리즘)
어떤 단방향 그래프 $G$의 모든 노드가 단 하나의 간선을 갖고 연결된 그래프라고 하자.
그러면 무조건 $\rho$ 모양의 그래프가 생긴다.
꼭 $\rho$ 모양이 아닐 수도 있고, 대략 다음과 같을 수도 있다.
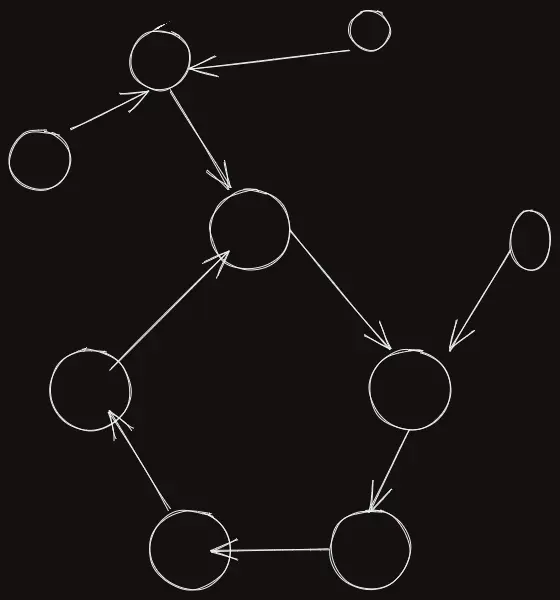
어쨌든 중요한건, 하나의 싸이클이 존재한다는 점이다!
이 싸이클에 들어있는 노드가 무엇인지, 싸이클의 길이가 얼마나 되는지 $O(N)$ 만에 찾을 수 있는 알고리즘이 바로 플로이드 알고리즘이다.
왜 토끼와 거북이 알고리즘이라고도 불리는 지 잠시 후 알아볼 수 있다.
꼭 싸이클이 있는 곳에서만 쓸 수 있는 알고리즘은 아니다. 오히려 싸이클의 유무를 판별하는 데도 쓰인다.
쓰이는 곳
저런 그래프의 싸이클을 찾는 것은 직접 DFS를 돌려 역방향 간선을 찾는 것으로도 가능하다.
따라서 사실 이 플로이드 알고리즘은 직접 그래프 탐색을 하는것으로 대체 가능한 알고리즘이다.
하지만 왜 의미가 있냐면, 위 영상에서 보듯이
- $O(N)$에 해결해야 하고
- 배열을 변경할 수 없고
- $O(1)$ 의 메모리에 해결해야 하는 (추가적인 자료구조 사용 불가)
조건들이 모두 충족될 수 있는 알고리즘이기 때문이다.
중복된 수 찾기
또한 이 알고리즘은 위와 같은 상황에 있는 그래프에서 중복된 두 수를 찾는데도 사용할 수 있다.
$0 \sim N-1$의 수들로 이루어진 $N+1$ 개의 수들 중, 어떤 한 수가 두 번 쓰였다고 할 때, 그 수를 찾아라
같은 문제를 해결할 수 있는데, 어떻게 동작하는지는 아래서 살펴보자.
알고리즘을 사용하는 법
원리를 살펴보기전에 그냥 먼저 어떻게 구현하는지를 알아보자.
일단 아무 시작점 $s$를 정한 다음에 $t, h$ 두 변수를 가지고 있다고 하자.
$t$는 한 번에 $f(t)$ 로 이동하고 $h$는 $f(f(h))$ 로 이동한다.
눈치챘겠지만 $t$는 tortoise로 거북이고, $h$는 hare로 토끼여서 각각 한 칸과 두 칸씩 이동한다.
이 동작을 반복하다보면 어느 순간 $t=h$ 인 시점이 오는데,
그 시점에 $t \coloneqq s$로 해주고 이제 $t, h$ 모두 한 칸씩만 이동하게 해주면 만나는 지점이 싸이클의 시작점이다.
이 시작점은 위에서 말한 문제의 중복된 수 이기도 하다.
원리
다음과 같은 그래프를 보자.
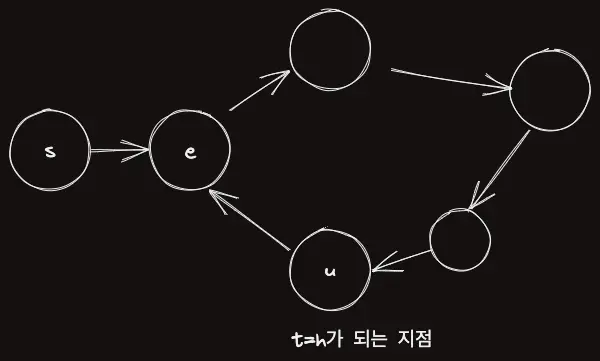
- $s$ : 시작 위치
- $u$ : $t=h$ 가 되는 지점
- $e$ : 싸이클의 시작
- $K_t$ : 거북이가 싸이클을 돈 횟수
- $K_h$ :토끼가 싸이클을 돈 횟수
처음에 $t,h$는 모두 $s$에 존재한다.
이제 $t \coloneqq f(t)$와 $h\coloneqq f(f(h))$ 를 반복하여 $t=h (=u)$가 되는 시점을 생각해보자.
여기서, $s \to u$ 라는 경로는 세 구간으로 나누어 볼 수 있다.
- $s \to e$ 구간 $A$
- $e \to u$ 구간 $B$
- $u \to e$ 구간 $C$
$B+C=\text{싸이클의 길이}$
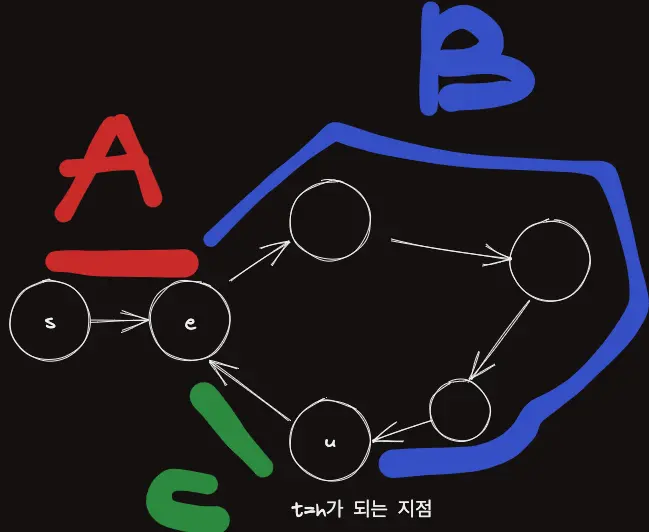
이때까지 $t$가 이동한 거리를 $T$, $h$가 이동한 거리를 $H$라고 하면,
$(1)$에서의 결론으로 다음과 같이 $A=C$ 의 유도가 가능하다.
즉, 결론적으로 $s$와 $u$에서 각각 한 칸씩 동일하게 이동하는 것으로 $e$에 같은 시점에 도달할 수 있다는 것이다.
코드
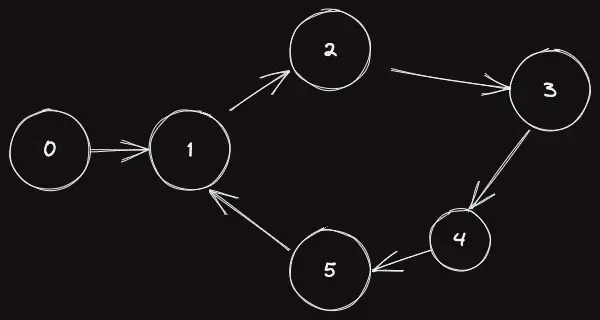
그래프를 구현한 것이다.
vi f(6);
f[0] = 1;
f[1] = 2;
f[2] = 3;
f[3] = 4;
f[4] = 5;
f[5] = 1;
int t = 0, h = 0;
do {
t = f[t], h = f[f[h]];
} while (t != h);
t = 0;
while (t != h) t = f[t], h = f[h];
cout << t; // 1
시간 복잡도
공간 복잡도는 다른 자료구조를 사용하지 않으므로 $O(1)$ 인건 알겠는데, 왜 시간복잡도가 $O(N)$ 일까?
일단 $t$와 $h$둘다 싸이클에 들어왔다고 생각해보자. $t$는 그 시점에서 싸이클을 한 바퀴 돌기전에 무조건 $h$와 만나게 된다.
그러므로 노드의 수에 비례해 $O(N)$이란 시간복잡도가 나온다.
1부터 N까지 수들 중 중복된 수 찾기
위에 구현한 것은 그래프였고, 이제 앞에서 언급했던 이 문제를 풀어보자.
$0 \sim N-1$의 수들로 이루어진 $N+1$ 개의 수들 중, 어떤 한 수가 두 번 쓰였다고 할 때, 그 수를 찾아라
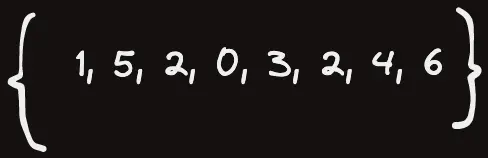
여기서, 이걸 배열로 나타내보자.
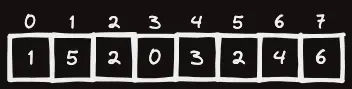
이제 $f(0)=1,\,f(1)=5,\, \dots$ 와 같이 표현을 할 수 있는데, 이걸 그대로 알고리즘으로 적용하면 된다.
vi f(8);
f[0] = 1;
f[1] = 5;
f[2] = 2;
f[3] = 0;
f[4] = 3;
f[5] = 2;
f[6] = 4;
f[7] = 6;
int t = 0, h = 0;
do {
t = f[t], h = f[f[h]];
} while (t != h);
t = 0;
while (t != h) t = f[t], h = f[h];
cout << t; // 2
정답인 $2$가 잘 나왔다.



Comments