$2$차원 배열에서 배열을 돌리거나 어떤 축에 대해 대칭시키는 등, 여러가지 연산들을 구현하는 법을 살펴본다.

이 글에서 다루는 숫자는 모두 $0-\text{based}$ 인덱스로 다루어진다.

배열 돌리기Permalink

배열을 돌리는 문제는 흔하다.

일단 이 섹션에서는 $90\degree$만 돌리는 법을 살펴본다.

$-90\degree(=270\degree)$ 나 $180\degree$는 $90$를 돌리는 것을 $k$번 반복해서 수행할 수 있다.

$180\degree$는 코드로 굳이 짜지 않고 $90\degree$와, $-90\degree$ 정도만 알아보도록 하겠다.

$N \times N$ 처럼 정사각 배열이면 코드가 좀 더 단순하지만, $N \times M ~(N \ne M)$ 여도 조금만 수정해주면 가능하다.

배열 $90 \degree$ 돌리기Permalink

$N = M$ 일 때를 보자정사각형.

$(y, x)$는 어디로 갈까?

편의를 위해 글에서 모든 배열의 인덱스는 $(y, x)=(\text{row}, \text{column})$로 설명한다.

위에서 $N=M=8$이고, $(1, 2)$에 $O$가 있다.

결론적으로 $(1,2) \to (2,6)$ 으로 가고, 다음과 같다.

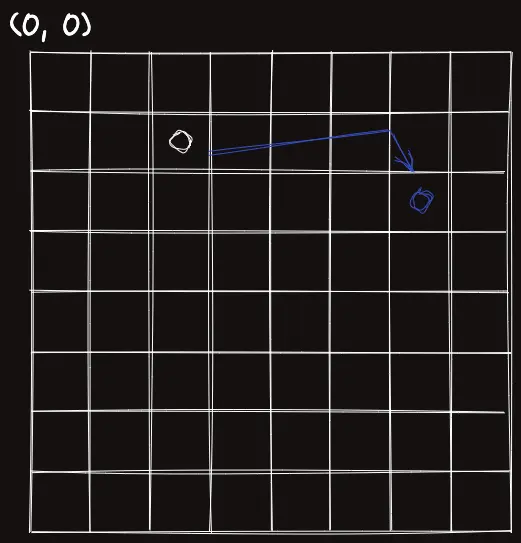
보면 다음과 같은 공식을 유도할 수 있다.

회전된 후의 $(y, x)$를 $(y', x')$라 할 때,

이는 $N \ne M$ 일 때도 동일하다.

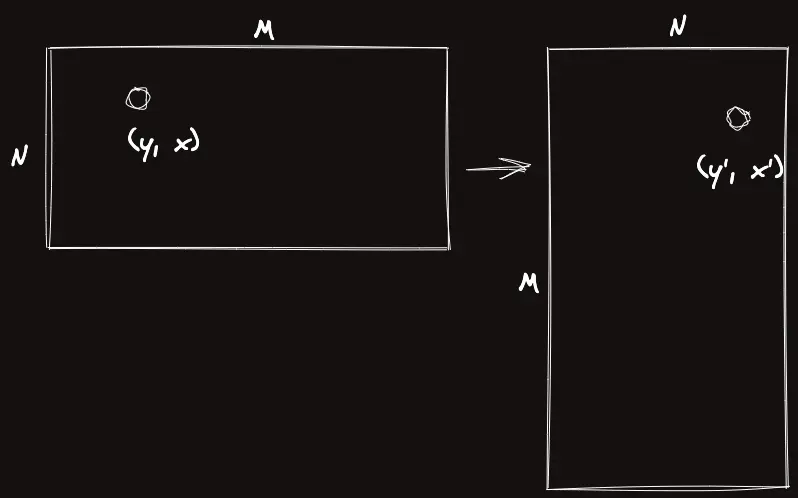
코드로 나타내면 다음과 같다.

vvi rotate_90(const vvi &b) {  
   int n = sz(b), m = sz(b[0]);  
   vvi ret(m, vi(n));  
   for (int y = 0; y < n; y++)  
      for (int x = 0; x < m; x++)  
         ret[x][n - 1 - y] = b[y][x];  
   return ret;  
}

결과는 다음과 같다.

13  8  8 
 7  5 13 
15  1  3 
10  3  8 
 9 14 15 

 9 10 15  7 13 
14  3  1  5  8 
15  8  3 13  8 

배열 $-90 \degree$ 돌리기Permalink

$-90\degree$를 회전시키는 것은 $90\degree$를 $3$번 회전시켜도 되지만, 조금 최적화를 하고싶다면 직접 구현해줄 수 있다.

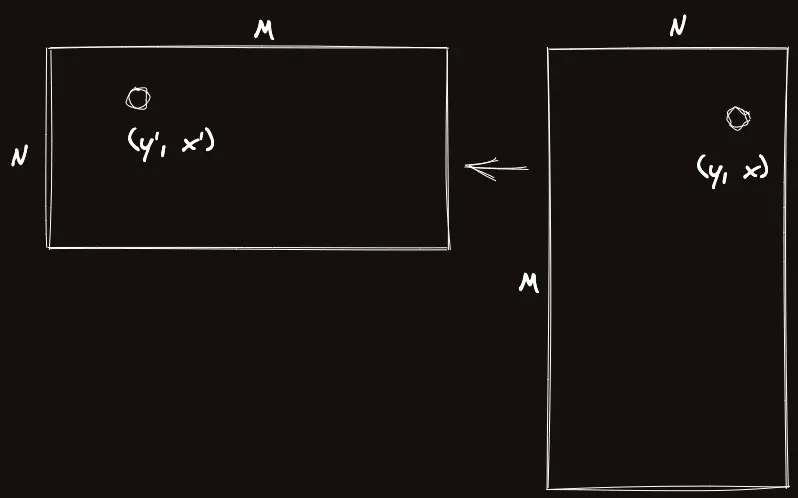
여기서의 식은 다음과 같다.

따라서 코드는 다음과 같다.

vvi rotate_90_reverse(const vvi &b) {  
   int n = sz(b), m = sz(b[0]);  
   vvi ret(m, vi(n));  
   for (int y = 0; y < n; y++)  
      for (int x = 0; x < m; x++)  
         ret[m - 1 - x][y] = b[y][x];  
   return ret;  
}

 5 13  1 
 2 15  0 
 6  7  9 
 0  3 12 
13  3  4 

 1  0  9 12  4 
13 15  7  3  3 
 5  2  6  0 13 

배열 돌리기는 공식을 외우지 않아도 그냥 직사각형을 그려보고 각 $y, x$가 어떻게 변환되는지 살펴보면서 식을 유도하면 된다.

배열 돌리기 관련 템플릿을 첨부한다.

template<class T>  
void rot(vector<vector<T>> &b, bool cw = 0) {  
   int r = sz(b), c = sz(b[0]);  
   auto t = vector<vector<T>>(c, vector<T>(r));  
   for (int i = 0; i < r; i++)  
      for (int j = 0; j < c; j++)  
         t[!cw ? j : c - 1 - j][!cw ? r - 1 - i : i] = b[i][j];  
   b = t;  
}  
template<class T>  
void rot_partial(vector<vector<T>> &b, int y1, int x1, int y2, int x2, bool cw = 0) {  
   int r = y2 - y1 + 1, c = x2 - x1 + 1;  
   assert(r == c);  
   auto t = vector<vector<T>>(r, vector<T>(c));  
   for (int i = 0; i < r; i++)  
      for (int j = 0; j < c; j++)  
         t[!cw ? j : c - 1 - j][!cw ? r - 1 - i : i] = b[y1 + i][x1 + j];  
   for (int i = 0; i < r; i++) for (int j = 0; j < c; j++) b[i + y1][j + x1] = t[i][j];  
}  
template<class T>  
void rotate_col(vector<vector<T>> &b, int x, int m, int rev = 0) {  
   vector<T> tmp(sz(b));  
   for (int i = 0; i < sz(b); i++) tmp[i] = b[i][x];  
   for (int i = 0; i < sz(b); i++) b[i][x] = tmp[md(sz(b), rev ? i - m : i + m)];  
}  
template<class T>  
void rotate_row(vector<vector<T>> &b, int y, int m, int rev = 0) {  
   if (!rev) rotate(b[y].begin(), b[y].begin() + m % sz(b[y]), b[y].end());  
   else rotate(b[y].begin(), b[y].begin() + (sz(b[y]) - m % sz(b[y])), b[y].end());  
}

배열 대칭시키기Permalink

중앙에서 수직선 대칭Permalink

$y$ 축과 평행하게 중앙을 기준으로 대칭시켜보자.

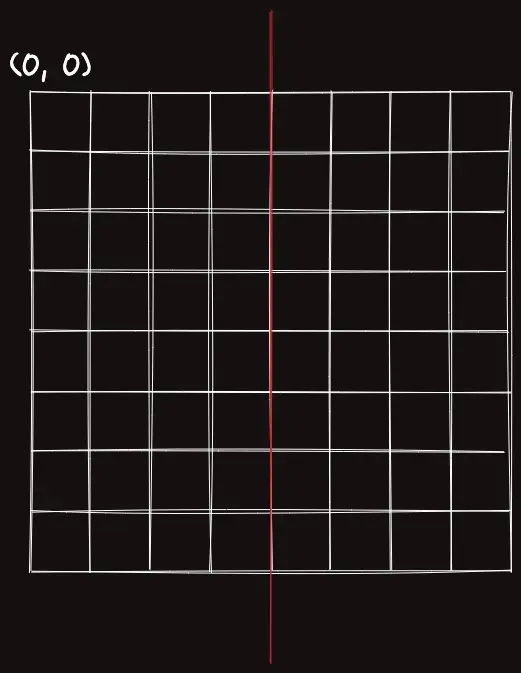
굳이 $2$차원 배열이라고 생각 안하고 $1$차원이라고 생각하면,

$M$ 길이의 배열일 때,

이다.

따라서 그냥 모든 $b[y][x]$ 값을 $b[y][M-1-x]$ 로 바꿔주는 것으로 충분하다.

코드로 나타내면 다음과 같다.

vvi flip_x_center(const vvi &b) {  
   int n = sz(b), m = sz(b[0]);  
   vvi ret(n, vi(m));  
   for (int y = 0; y < n; y++)  
      for (int x = 0; x < m; x++)  
         ret[y][x] = b[y][m - 1 - x];  
   return ret;  
}

 3 13 10  2  0  6 
15  0  0  9  5  2 
 1  3  6  7 11  0 

 6  0  2 10 13  3 
 2  5  9  0  0 15 
 0 11  7  6  3  1 

중앙 $x$축 대칭은 $y$에 대해서 동일하게 $N-1-y$로 바꿔주면 되므로 설명을 생략하도록 하자.

중앙점 대칭Permalink

중앙점 대칭은, 위에서 했던걸 $y, x$에 대해 모두 해준다고 생각하면 된다.

vvi flip_center(const vvi &b) {  
   int n = sz(b), m = sz(b[0]);  
   vvi ret(n, vi(m));  
   for (int y = 0; y < n; y++)  
      for (int x = 0; x < m; x++)  
         ret[y][x] = b[n - 1 - y][m - 1 - x];  
   return ret;  
}

 7 14  9 12 10 
 6  1  9  1 12 
 9  7 11 11  4 
 9  1 15  7  4 

 4  7 15  1  9 
 4 11 11  7  9 
12  1  9  1  6 
10 12  9 14  7 

대각선 대칭Permalink

이 대칭들은 정사각배열이 아니면 적용할 수 없다.

$y=x$ 에 대해 대칭시켜보자.

고등수학에서도 배우듯이 $y=x$에 대해 대칭시킨 것은 역함수이고, $y$와 $x$를 바꿔주기만 하면 된다.

vvi flip_y_equals_x(const vvi &b) {  
   int n = sz(b), m = sz(b[0]);  
   vvi ret(n, vi(m));  
   for (int y = 0; y < n; y++)  
      for (int x = 0; x < m; x++)  
         ret[y][x] = b[x][y];  
   return ret;  
}

 5  3  7  9 
14 15  7  4 
13 15  4  1 
 6  3  8  0 

 5 14 13  6 
 3 15 15  3 
 7  7  4  8 
 9  4  1  0

결과가 의아하다면 왼쪽 위가 $(0, 0)$좌표라서 그렇다.

기울기가 $-1$ 인 대각선이랑 대칭을 시키려면 그 대각선은 $y=-x$가 아닌 $y=-x+N-1$ 이라 해야 맞다.

따라서 이걸 적절히 변환해주면 다음과 같다.

vvi flip_y_equals_minus_x(const vvi &b) {  
   int n = sz(b), m = sz(b[0]);  
   vvi ret(n, vi(m));  
   for (int y = 0; y < n; y++)  
      for (int x = 0; x < m; x++)  
         ret[y][x] = b[n - 1 - x][n - 1 - y];  
   return ret;  
}

 3 13 13  1 
 4  2  2 10 
 2 10 15 13 
13  4  0  1 

 1 13 10  1 
 0 15  2 13 
 4 10  2 13 
13  2  4  3 

Bonus - 배열 45$\degree$ 돌리기Permalink

배열을 $45\degree$ 돌린다는 것은 다음과 같다.

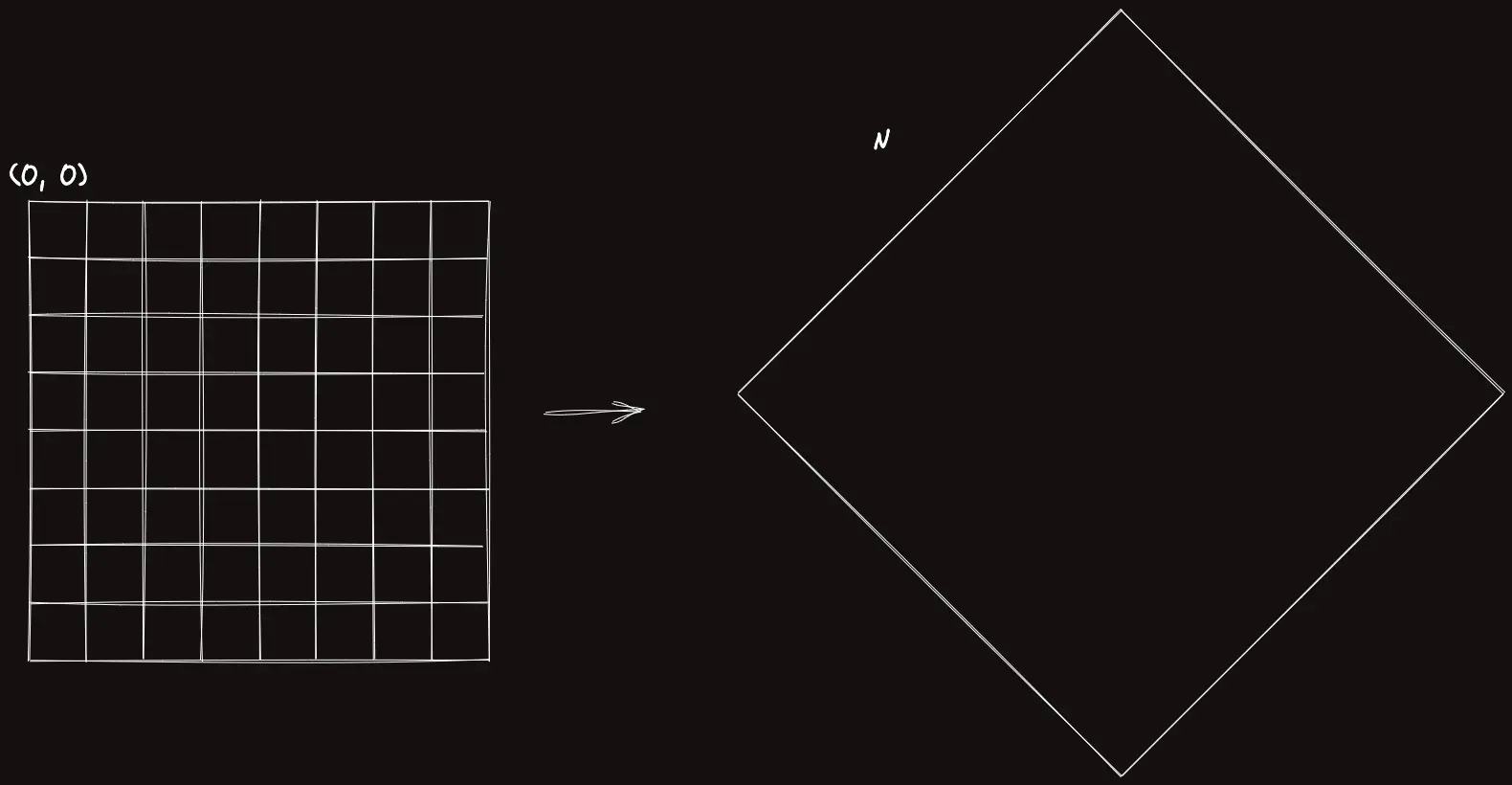
$N \times N$ 크기의 배열이라면, $2N-1 \times 2N-1$ 로 크기가 정해진다.

배열을 $45\degree$를 돌려 어디다가 쓸 수 있냐면, 다이아몬드(기울어진 사각형) 모양의 어떤 영역에 대해 연산을 처리해줌에 있어, 이걸 $2$차원에서 직사각형으로 다루어줄 수 있다는 장점이 있다.

BOJ 1028 - 다이아몬드 광산 같은 문제에 유용하다.

물론 시간 복잡도는 $4$배까지 늘어날 수 있다.

$(0, 0)$이 $(0, N-1)$로 가게 한다면 $45\degree$를 돌리는 것이고,

$(0,0)$이 $(N-1, 0)$이 된다면 $-45\degree$를 돌리는 것이라고 볼 수 있다.

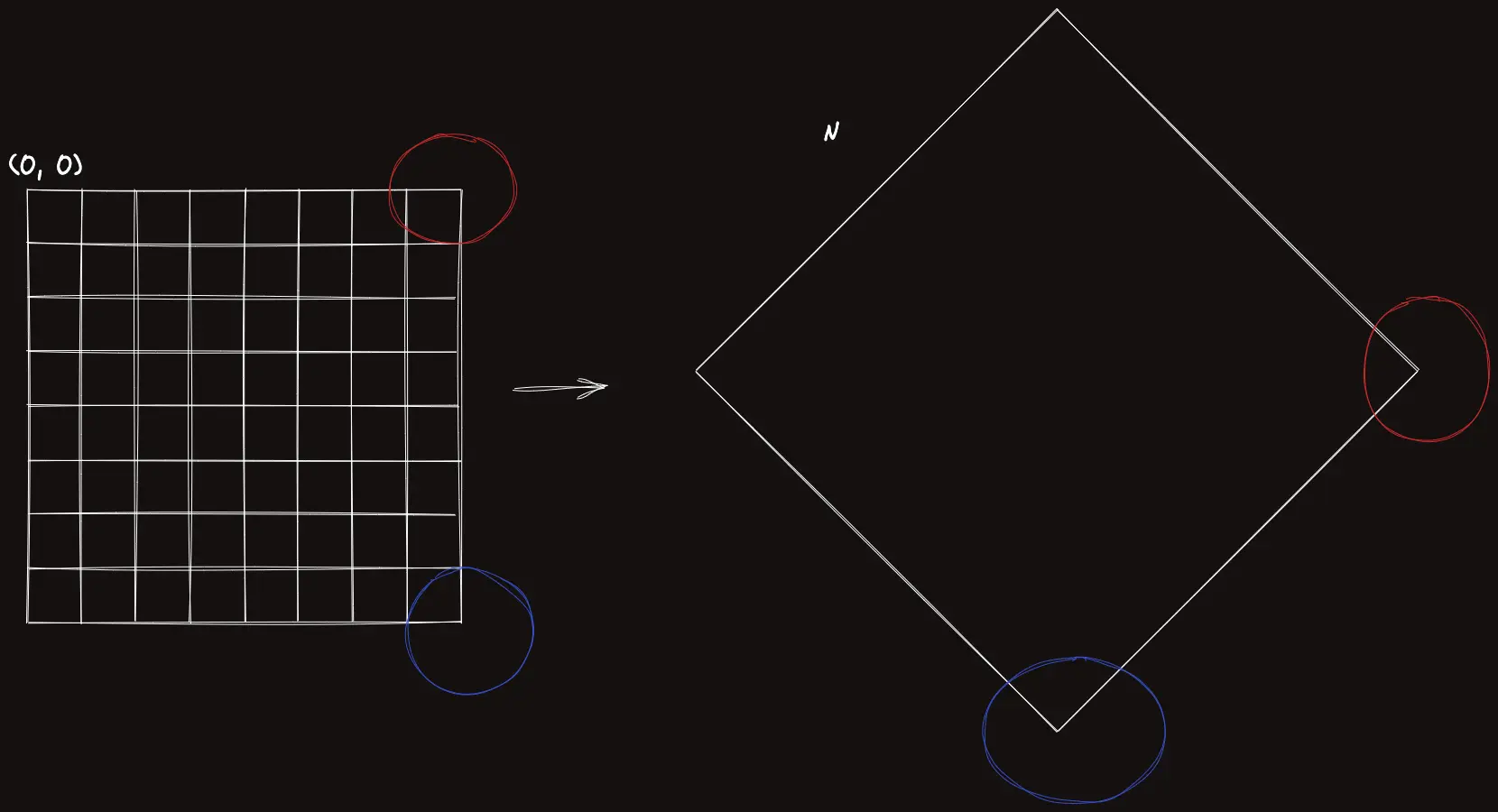
이렇게 두 점이 어떻게 변하는지만 보면 식을 유도해내기 쉽다.

일단 파란점이 제일 아래쪽으로 간다는 것은 $y'$ 값이 최대이려면 $y+x$가 최대여야 한다는 의미이므로, $y'=y+x$ 이다.

빨간점이 제일 오른쪽으로 간다는 것은, $x'$ 값이 최대이려면 $N-1-y+x$ 가 최대여야 한다는 의미이므로, $x'=N-1-y+x$ 이다.

vvi rotate_45(const vvi &b) {  
   int n = sz(b);  
   vvi ret(n * 2 - 1, vi(n * 2 - 1));  
   for (int y = 0; y < n; y++)  
      for (int x = 0; x < n; x++)  
         ret[y + x][n - 1 - y + x] = b[y][x];  
   return ret;  
}

10 10 18 10 
14 11 20 17 
19 13 16 18 
12 14 20 16 

 0  0  0 10  0  0  0 
 0  0 14  0 10  0  0 
 0 19  0 11  0 18  0 
12  0 13  0 20  0 10 
 0 14  0 16  0 17  0 
 0  0 20  0 18  0  0 
 0  0  0 16  0  0  0

$-45\degree$ 돌리는 것은

가 된다.