스털링 수Permalink

스털링 수는 조합론에 나오는 개념으로 두 가지 종류가 있다. PS에도 관련된 문제가 나온다.

하나씩 알아보자.

제 1종 스털링 수 - 순열의 분할Permalink

어떤 $n$개의 수를 $k$개의 순열로 만드는 경우의 수이다.

$s(n,k)$ 처럼 표현하며 점화식은 다음과 같다.

이 점화식이 나오는 이유는 다음과 같다. 사진을 보자.

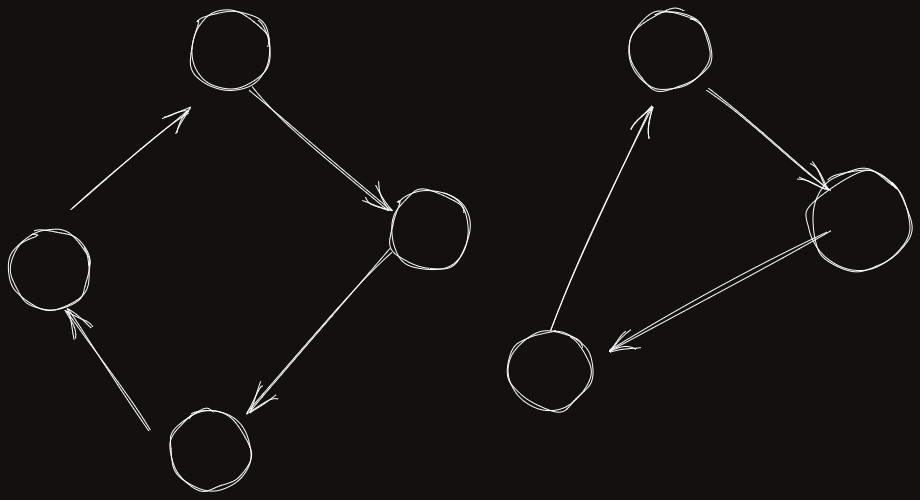
만약 $n$번째 원소로 새로운 순열 그룹을 만든다면 다음과 같이 추가가 된다.

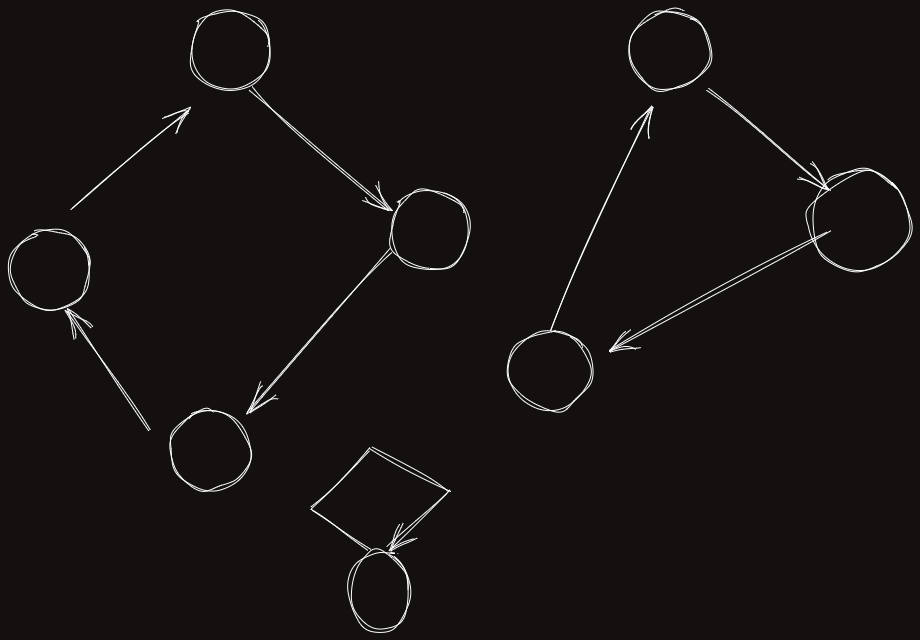
따라서 $s(n-1,k-1)$ 이 더해진다.

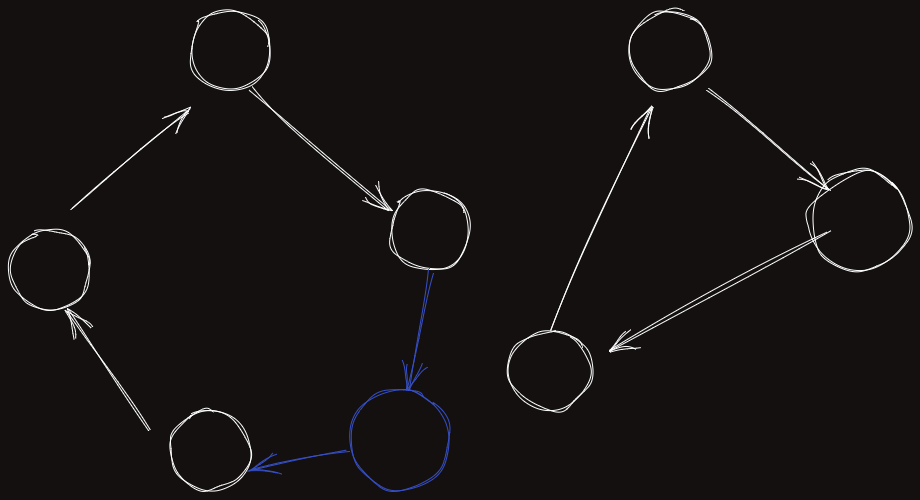
혹은 이 새로운 원소를 이미 존재하는 순열 중 하나에 넣는다면, 어떤 간선 $u \to v$ 에 넣어야 하는데, 그러한 간선은 항상 $n-1$ 개이므로 그 중 하나를 골라서 삽입시킬 수 있다. 그래서 $(n-1) \cdot s(n-1,k)$ 가 더해진다.

연습 문제Permalink

BOJ 1413 - 박스 안의 열쇠

제 2종 스털링 수 - 집합의 분할Permalink

어떤 $n$개의 수를 $k$개의 집합으로 분리하는 경우의 수이다.

수식으로 $S(n, k)$로 나타낸다.

점화식은 다음과 같다.

첫 항은 $n$번째 원소를 아예 새로운 집합안에 첫 번째 원소로 집어넣는 것으로, 기존에는 $k-1$ 개의 집합이 있었기 때문에 $S(n-1, k-1)$가지 경우를 더해주는 것이고,

두번째 항은 현재 이미 $n-1$ 개의 원소들로 $k$개의 집합을 만든 상태에서 $n$번째 원소를 그 중 하나에 넣는 경우의 수로, 집합이 $k$개가 있으니까 $k$를 곱해서 $k \cdot S(n-1, k)$를 더해준 것이다.

이 테이블을 채우는 것은 $O(n^2)$ 이다.

기저는 $S(0, 0)=1$ 로 초기화 해주면 된다.

연습 문제Permalink

BOJ 20531 - 인간 관계