Divide & Conquer Optimization
Prerequisite
Divide & Conquer Optimization
분할정복 최적화는 정말 분할 정복테크닉을 이용해 특별한 점화식의 꼴을 가지며 특별한 조건을 만족하는 DP문제를 더 빠른 시간복잡도로 해결하는 테크닉이다.
하지만 따로 DP테이블을 선언해서 사용하지 않을 수도 있고, 이 자체로 어떠한 문제의 해를 찾는데 쓰이기도 한다. 아래 문제에서 살펴볼 것이다.
점화식
점화식은 다음과 같은 꼴을 갖는다.
$i<0$이나 $j<0$ 등 예외사항들은 문제에 따라 적절히 처리해줄 수 있다.
$x,y,z$ 항들은 문제에 따라 존재할 수도, 존재하지 않을 수도 있다.
$i \le N, j \le M$ 이라고 하자. 위 점화식에서 $dp(N, M)$을 해결하는 시간복잡도는 $x,y,z$의 시간복잡도를 신경쓰지 않고($O(1)$이라고 생각하고) 원래대로라면 $O(NM^2)$ 이지만, 이 최적화를 사용하면 $O(NM \log M)$의 시간복잡도가 가능하다.
조건
점화식의 꼴이 위와 같다고 항상 적용할 수 있는 것은 아니고, 다음과 같은 조건이 성립되어야 한다.
$opt(i, j)$를 $dp(i, j)$가 최적의 값이 되게 만드는 $k$값이라고 할 때,
처럼 최적해의 단조성이 있어야 한다.
$c$ 함수가 Monge arrayquadrangle inequality면 이 조건이 충족되지만, 역은 성립하지 않는다.
Monge Array $\to$ 최적해의 단조성이 충족되는 이유는 이 글을 참고하자.
따라서 이걸 가지고 DnC Opt를 쓸 수 있다고 쉽게 판단할 수 있다.
그러나 최적해의 단조성이 있으면 $c$가 Monge array가 아니여도 이 최적화가 성립한다.
Monge Array
Monge Array의 정의는 다음과 같다.
$a \le b \le c \le d$ 일 때, $C(a,c) + C(b,d) \le C(a,d)+C(b,c)$
다른 구간을 완전히 포함하지 않는 형태가 되게 만들어줄 때 더 최적의 값이 나온다라는 뜻인데, 따라서 중간의 부등호의 방향은 문제에 따라 최소값, 최대값을 구하는지에 따라 다르게 생각해주어야 한다.
위의 꼴은 포함되지 않는 형태가 작거나 같은 값을 가지므로 최소값을 찾는 문제에서 저렇게 사용하고, 최대값을 찾는 문제에선 반대여야 한다.
더 자세한 글은 Monge Array 를 참고하자.
과정
이 최적화가 왜 타당하게 진행되는지는 $opt(i, j) \le opt(i, j+1)$를 만족하면 별다른 증명이 필요없이 과정을 살펴보며 알 수 있다.
즉, 우리가 보통 문제를 풀 때, 해야하는 증명들은 최적해의 단조성이 왜 타당한지에 대하여 직접 생각하거나 Monge Array같은 친구를 찾으면 된다.
과정을 살펴보기전에 조금 문제를 단순히 생각해 볼 필요가 있다.
원래 점화식을 보자.
여기서 $i=0$ 라고 가정해보면 $x(i,k)$ 라는 값은 문제에 따라 동일한 상수가 되는데, 그럼 $i$에 대한 컨텍스트가 사라져서
처럼 생각해줄 수 있다.
여기서 $opt(j)$에 단조성이 있다는 건 $j$가 증가함에 따라 결국 $c(k, j)$ 값에 단조성이 있다는 뜻이다.
$y(j)$는 $k$랑 관련없이 없고 $z(k)$ 또한 그렇기 때문에 무시해줄 수 있다.
이렇게 문제를 단순화시키고 모든 $j~(j \le M)$에 대해 $dp(j)$를 채워보자.
우선, $dp(M/2)$를 $O(M)$으로 구하고 $opt(M/2)$을 찾을 수 있을 것이다.
$a<b \to opt(a) \le opt(b)$라 한다면, $dp(0) \sim dp(M/2)$ 까지의 최적해는 절대 $opt(M/2)$을 넘을 수 없다.
마찬가지로 $dp(M/2) \sim dp(M)$까지의 최적해는 절대 $opt(M/2)$ 미만일 수 없다.
그럼 또 $dp(0) \sim dp(M/2)$ 에서 $M/4$를 선택하여 $opt(M/4)$를 구하고 $dp(0) \sim dp(M/4)$ 와 $dp(M/4) \sim dp(M/2)$ 까지의 최적해를 구하는 과정으로 재귀적인 수행이 반복된다.
이 과정의 총 시간복잡도는 마스터 정리에 의해 $O(M \log M)$이다.
마스터 정리 Master Theorem
어떤 알고리즘의 시간 복잡도 함수 $T(n)$이 다음과 같은 형태일 때,
$a,b,d$는 상수, $a>0, b \ge 2, d \ge 0$
$T(n)$의 시간복잡도는 다음과 같다.
$a$는 나뉘어지는 문제의 개수, $b$는 나뉜 후 문제의 크기, $d$는 나뉠 때 드는 시간복잡도이다.
위에 대입시켜보면 $a=b=2$이고, $d=1$ 이므로, 두 번째 case에 해당되어 $T(n)=O(n \log n)$ 이 됨을 알 수 있다.
따라서 원래 점화식 $dp(N, M)$는 $i =0 \to i=N$에 대해 한 단계씩 크게 반복이 된다고 생각하면 된다.
이런 과정을 $N$번 반복하기 때문에 우린 $O(NM \log M)$에 원래 풀려던 문제의 정답을 구할 수 있게 된 것이다.
팁은 $i = 0 \to i = N$에 대해 진행하므로 $M$의 값이 커도 토글링을 이용해 공간복잡도를 줄일 수 있다.
연습 문제
BOJ 11001 - 김치
문제를 보자.
김치의 맛은 (숙성 시간) * (김치를 꺼낼 때의 온도) + (김치를 넣은 날 가치) 라고 한다.
현재를 $i$, 김치를 넣은 날짜를 $j$라고 한다면,
$d_i$가 최적이 되는 $j$값을 $opt(i)$라고 하면, $opt(i) \le opt(i+1)$ 이다.
왜냐면 저 식 자체가 Monge Array이기 때문인데, 식을 전개해보자.
왜냐면 위 식에서 $i \cdot t_i$는 $i$에 관련된 값이라 $j$랑 상관이 없고, $v_j$도 $j$랑 관련된 값이라 상관이 없다.
따라서 단순히 $C(l,r)=-lt_r$ 이라 하자.
이 문제는 최대값을 찾는 문제이므로
$a \le b \le c \le d$라 할 때, $C(a,c)+C(b,d) \ge C(a,d)+C(b,c)$를 전개해보면,
여기서 $b-a \ge 0$ 이고, 문제의 정의에 따라 $t_d - t_c \le 0$ 이므로 식이 성립한다. 즉, $C$는 Monge array이다.
이 문제는 $dp(i, j)$가 아닌 $dp(i)$ 만 구하는 것이기 때문에 실제로 $dp$ 를 정의할 필요가 없다.
즉, $N=1$ 인 경우라고 볼 수 있다.
일반화된식에 적용해보면,
$N=1$ 이기 때문에
이고,
- $c(k,j)=-kt_j$
- $y(j)=jt_j$
- $z(k)=v_k$
이다.
이제 직접 구현해보자.
구현법은 전형적이므로 해보다보면 암기가 자연스레 된다.
void solve() {
int n, d;
cin >> n >> d;
vi t(n), v(n);
fv(t);
fv(v);
int ans = 0;
function<void(int, int, int, int)> fn = [&](int l, int r, int optl, int optr) -> void {
if (l > r) return;
int m = (l + r) / 2;
int opt = optl, value = -1;
for (int o = max(optl, m - d); o <= min(optr, m); o++) {
int tmp = (m - o) * t[m] + v[o];
if (tmp > value) {
value = tmp;
opt = o;
}
}
ans = max(ans, value);
fn(l, m - 1, optl, opt);
fn(m + 1, r, opt, optr);
};
fn(0, n - 1, 0, n - 1);
cout << ans;
}
BOJ 13261 - 탈옥
이제 $N > 1$ 인 경우에 대해서 실제 $dp$ 테이블이 필요한 문제를 풀어보자.
문제에서 요구하는 점화식은 다음과 같다.
$dp[G][L]$을 $G$명의 간수가 앞에서부터 $L$개의 칸을 관리할 때 탈옥 위험도의 최소값이라고 하자.
그리고 $P_i$를 $P_i = \displaystyle \sum_{j=0}^i C_j$ 라고 정의하자 (구간합 배열)
위에 두 개는 예외케이스 격이고, 마지막 식이 점화식이다.
또 일반화된 식을 가져와보자.
보면 $x(g,k)=dp[g-1][k]$ 이고, $c(k,l), y(l), z(k)$ 도 각각 구할 수 있을 것이다.
$c(k,l)=-kP_l-lP_k$ 이다.
최소값을 찾아야 하므로 $c(a,c) + c(b,d) \le c(a,d) + c(b,c)$ 임을 보이자.
$P$는 구간합 배열이라 $P_d-P_c \ge 0$ 이므로 $c$는 Monge Array이다.
이제 구현해보자.
const int inf = 4e18;
void solve() {
int L, G;
cin >> L >> G;
vi R(L + 1), P(L + 1);
vvi dp(G + 1, vi(L + 1, inf));
for (int i = 1; i <= L; i++) {
cin >> R[i];
P[i] = P[i - 1] + R[i];
}
// g = 1
for (int l = 1; l <= L; l++) dp[1][l] = l * P[l];
function<void(int, int, int, int, int)> fn = [&](int g, int left, int right, int opt_left, int opt_right) -> void {
if (left > right) return;
int mid = (left + right) / 2;
int opt = opt_left;
if (g > mid) {
dp[g][mid] = P[mid];
fn(g, left, mid - 1, opt_left, opt_right);
fn(g, mid + 1, right, opt_left, opt_right);
} else {
for (int k = max(opt_left, g - 1); k <= min(opt_right, mid - 1); k++) {
int tmp = dp[g - 1][k] + (mid - k) * (P[mid] - P[k]);
if (tmp < dp[g][mid]) {
opt = k;
dp[g][mid] = tmp;
}
}
fn(g, left, mid - 1, opt_left, opt);
fn(g, mid + 1, right, opt, opt_right);
}
};
for (int g = 2; g <= G; g++) fn(g, 1, L, 1, L);
cout << dp[G][L];
}
BOJ 14636 - Money for Nothing
문제를 읽어보면 p와 q를 x좌표로 잡고 d와 e를 y좌표로 잡아서 가장 큰 사각형의 넓이를 찾는 것임을 알 수 있다.
단, (q, e)가 사각형의 오른쪽 위 꼭지점이여야 한다.
$C\left[i\right]\left[j\right]=\left(consumer\left[i\right].q-producer\left[j\right].p\right)\left(consumer\left[i\right].e-producer\left[j\right].d\right)$
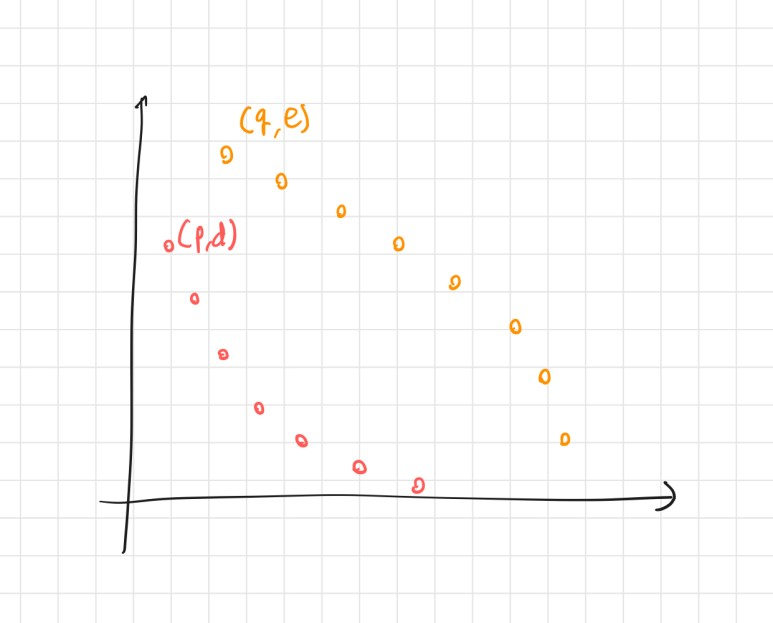
이렇게 (p, d)와 (q, e) 모두 y값이 단조감소 하는형태로만 점들을 솎아낸다고 하자.
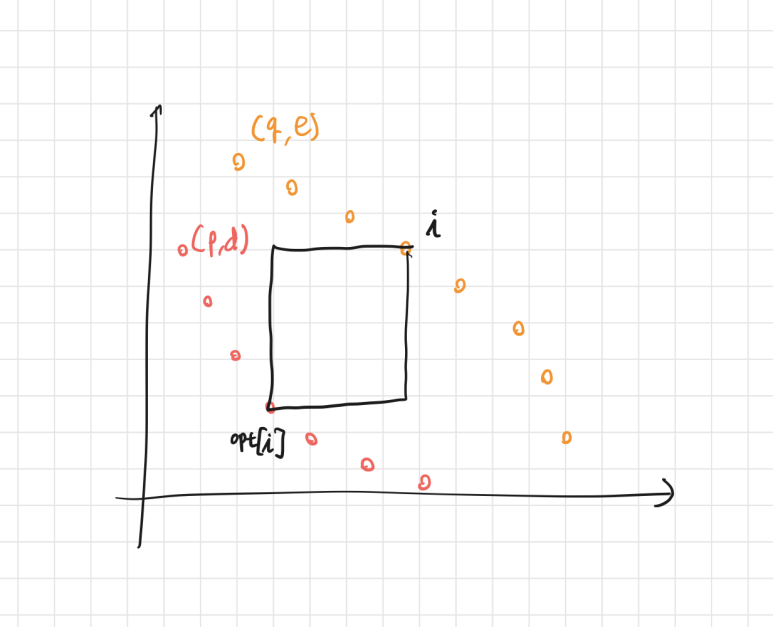
여기서 최적해의 단조성을 증명해보자.
어떤 i번째 consumer가 가장 큰 직사각형을 만드는 producer를 opt[i] 라고 할 때,
opt[i+1] <= opt[i] 이다.
이는 직사각형의 넓이에 대해 monge array가 나타난다는 것을 보이면 된다.
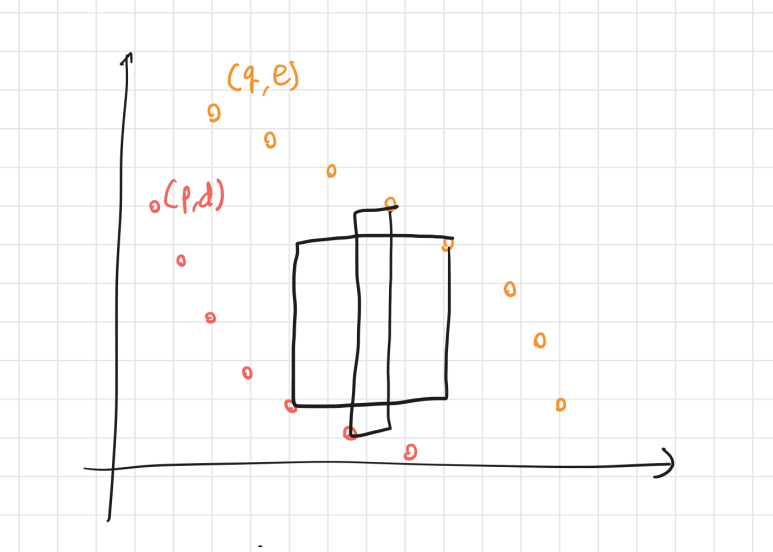
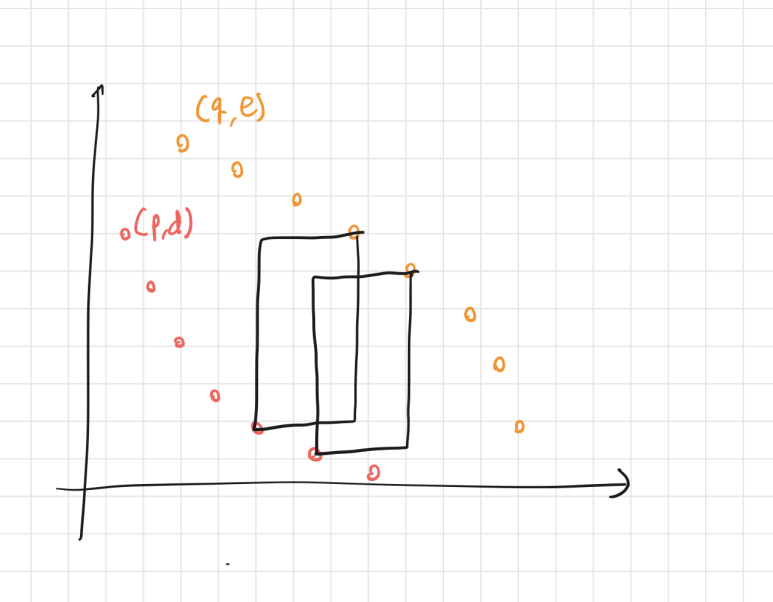
두 번째 그림의 사각형 넓이의 합이 첫 번째 그림의 합 이상이라는 것을 보이자.
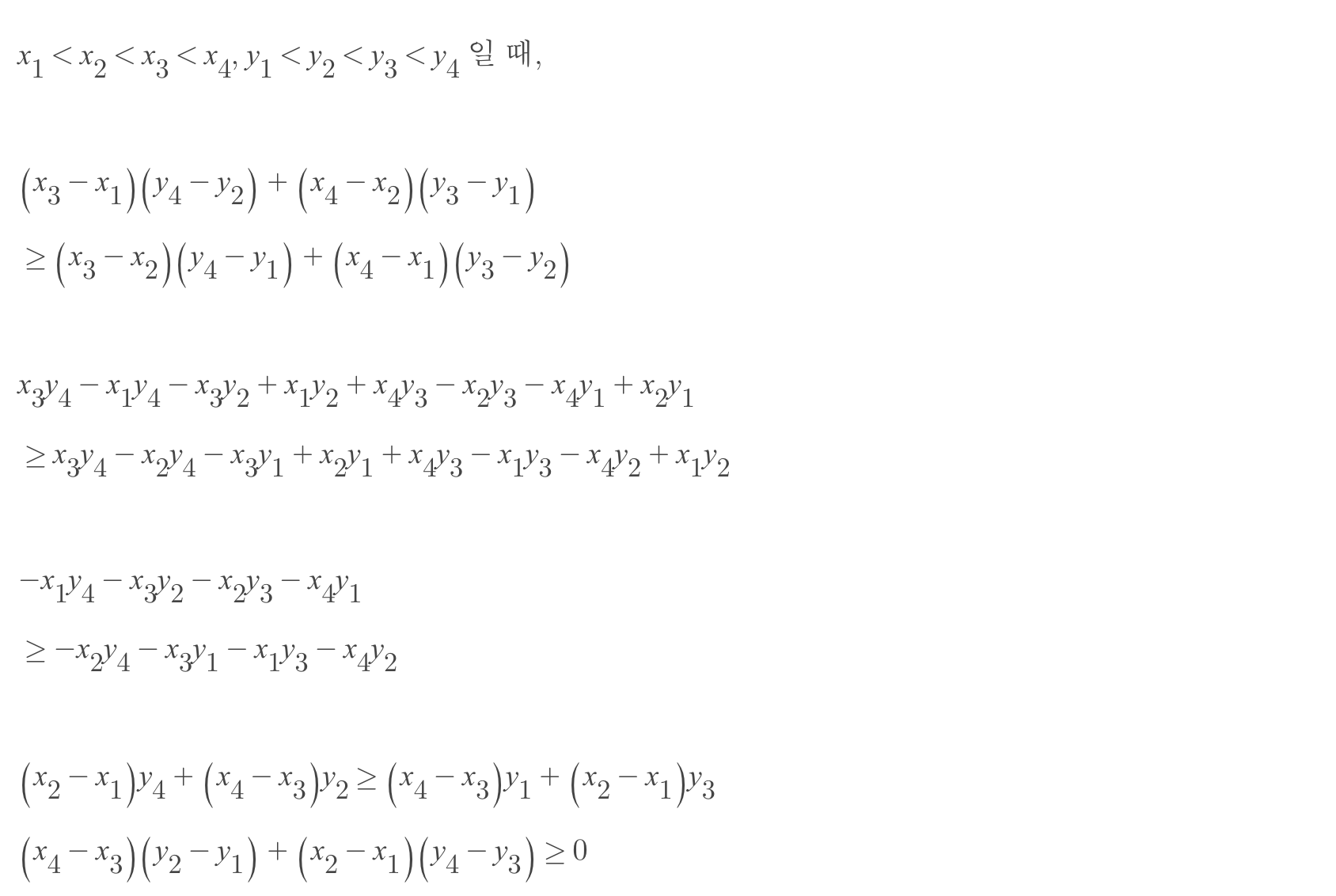
하여튼 이래서 직사각형의 넓이가 Monge Array라서 최적해의 단조성을 보일 수 있다.
BOJ 18444 - 우체국 3
시간복잡도 $O(V \cdot PV \log V)$ 에 해결할 수 있다.
우선 모든 마을을 시작점으로 한 번씩 DP를 수행한다고 할 때, $O(V)$이다.
그리고 분할정복 최적화를 쓰므로 $O(PV \log V)$가 붙었다.
$dp[p][v]=$ $p$개의 우체국을 써서 $v$번 째 마을에 마지막으로 우체국을 설치할 때 $0 \sim v$ 번째 마을까지 가장 가까운 우체국까지의 거리의 합
이라고 하자.
이고, $C[k][v]$는 $k+1 \sim v-1$ 번째 마을들을 보면 $k$와 더 가까운 마을이거나 $v$와 더 가까운 마을들인데, 각각 더 가까운 우체국쪽으로 거리들의 합이다.
이 $C[k][v]$는 투포인터와 구간합배열을 통해 전처리해두면 $O(V^2)$에 전처리하고 $O(1)$에 쿼리가 가능하다.
마지막으로 시작 마을 $s$에 대해 $dp_s[p][v]$를 구했다면 $v+1 \sim s - 1$ 까지의 마을들은 우리가 dp로 구한 범위 밖에 있는 마을들인데,
이 마을들도 각각 $s$나 $v$에 대해서 더 가까운 쪽으로 거리들의 합을 $O(1)$에 구해줄 수 있다.
$C$를 잘 전처리해두면 재사용할 수 있다.
따라서 $V \le 250$은 쉽게 통과가 가능하다.
우체국 4는 에일리언 트릭을 쓰거나 DnC opt를 쓰고 아주 잘 구현하고 랜덤 풀이를 써야한다. 여기서 100몇틀을 해서 아직 못풀었다. 푸는 방법은 아는데 구현을 하기 무섭다.



Comments