Centroid Decomposition
Centroid
트리의 Centroid의 정의는 다음과 같다.
어떤 정점을 루트로 봤을 때, 서브트리들의 크기의 최댓값이 최소가 되는 정점
Centroid의 유용한 성질은 항상 모든 서브트리의 크기가 $\dfrac N2$ 이하임이 보여진다는 것이다.
Centroid는 분할 정복을 이용해 구현되며 각 트리당 하나만 있는 것이 아닌 모든 서브트리가 하나로 분리될 때 까지 계속된다.
즉, 모든 노드가 결국엔 센트로이드가 된다.
트리에서 Centroid를 구하는 것은 분할정복을 이용하며, $N$ 개의 노드의 센트로이드를 찾는 과정의 시간복잡도는 $O(N)$ 이다.
모든 노드가 Centroid로 분리되기 까지의 시간복잡도는 $O(N \log N)$이다.
이는 마스터 이론으로 보여질 수 있다.
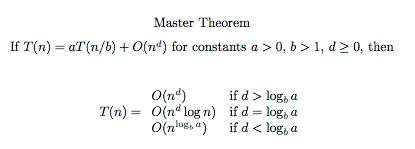
$a=b$ 는 서브트리의 개수이고 $d$는 이따 보겠지만 $d=1$이기 때문에 $O(N \log N)$이 나온다.
센트로이드가 어떤 친구들인지 그림과 함께 살펴보자.
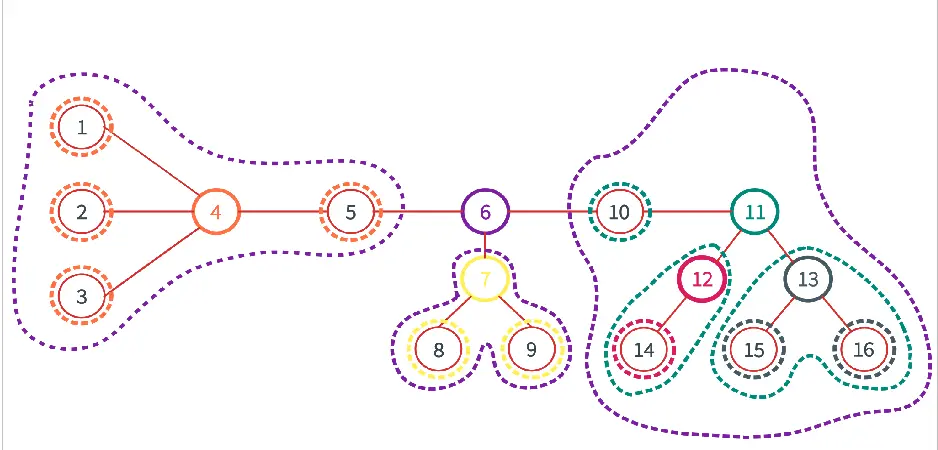
6번 정점이 모든 노드를 갖고 Centroid를 찾았을 때의 Centroid이고, 이제 또 나머지 묶인 부분들에서 각각 Centroid가 찾아지며, 결국 크기 1짜리의 Centroid들로 분해가 되며 알고리즘이 종료된다.
그림을 보면 알겠지만 각 Centroid들의 서브트리의 크기들 중 최댓값은 항상 최소이며, 그 크기들은 모두 트리의 크기의 절반 이하이다.
여담으로 Centroid Decomposition 은 트리에서 꽤나 사기적인 테크닉이기 때문에 굳이 이걸 안쓰고 트리 DP같은 알고리즘으로 풀 수 있는 문제에도 뇌절을 박아버리기 쉽다.
Centroid의 서브트리들의 크기에 대한 증명
트리에서 Centroid는 항상 존재하며, Centroid의 서브트리들의 크기는 항상 원래 트리 크기의 절반 이하이다. 그것을 증명하고 넘어가자.
$S_i$ 를 $i$번 정점을 트리에서 지웠을 때 나뉘어지는 서브트리들 중 가장 큰 크기라고 하자.
$S_i$가 $\left\lfloor \dfrac N2 \right\rfloor$이하가 되는 정점은 항상 존재한다.
$N$이 짝수이면 $\dfrac N2 -1$ 이하여야 하고, $N$이 홀수이면 $\dfrac {N-1}2$ 이하이다.
그렇지 않다고 하자. 어떤 트리 $G$ 는 어떠한 정점을 지워도 $S_i$가 $\left\lfloor \dfrac N2 \right\rfloor$초과라고 하자.
$G$에서 $S_i$가 최소인 정점 $u$가 있다고 하자.
$u$와 바로 인접한 어떤 정점 $v$를 루트로 하는 서브트리의 크기는 $\left\lfloor \dfrac N2 \right\rfloor$ 초과이다.
$v$가 없어져서 생긴 $u$를 루트로 하는 서브트리의 크기는 $\left\lfloor \dfrac N2 \right\rfloor$ 이하 여서 $S_v \le \left\lfloor \dfrac N2 \right\rfloor$ 이기 때문에 $S_u$가 가장 작다는 것에 모순이다.$\square$
Centroid Tree
Centroid Tree는 Centroid들을 가지고 원래의 트리를 재구성한 트리이다.
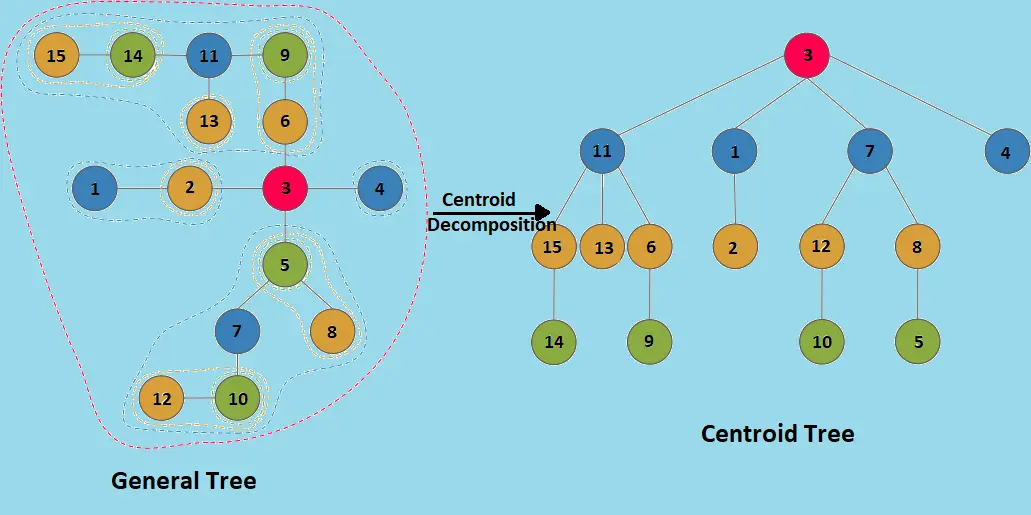
사실 Centroid Decomposition으로 풀 수 있는 문제들은 대부분 이Centroid Tree를 구성해서 성질을 활용하는 방식으로 푼다고 보면 된다.
센트로이드 트리의 성질
1. 항상 트리의 Level은 최대 $log N$에 상한이 있다.
센트로이드는 현재 서브트리에서 정점들을 모두 $\left\lfloor \dfrac N2 \right\rfloor$ 이하 크기의 서브트리들로 나누기 때문에 자명하다.
2. 센트로이드 트리에서 두 정점 $u, v$의 최소 공통 조상은 $\overline{uv}$ 경로를 분할한다.
기존 트리에서 $u, v$ 가 있다면, 센트로이드 트리에서 $LCA(u, v)$는 항상 기존 트리에서도 $u$와 $v$ 사이에 있다는 것이 보장된다.
3. 센트로이드 트리에서 어떤 정점 $u$에서 루트까지에 있는 정점들 $P_i$는 $u$에서 다른 정점으로의 경로와 관련된 쿼리에 사용될 수 있다.
이 성질은 아래서 더 자세히 살펴보자.
구현
Centroid Tree를 다룰 때 생각해야 할 점은, 이 개념 자체는 그냥 트리를 특별한 성질이 있는 트리로 재구성한다는 알고리즘이라는 것이다.
그 이후 그 성질들을 이용해 다른 자료구조나 알고리즘과 결합해서 문제를 해결할 수 있도록 한다.
알고리즘은 분할 정복을 이용해서 구현되고 순서는 다음과 같다.
- 현재 트리의 Centroid를 찾는다.
- 찾은 Centroid의 주변 노드들 중 이미 Centroid로 찾아지지 않은 서브트리들에서 재귀적으로 1번 과정을 진행한다.
단순하다.
이제 Centroid를 어떻게 찾는지를 알아보자.
Centroid를 찾는 함수는 항상 현재 서브 트리의 크기를 가지고 다닌다.
따라서 방문되지 않은 정점들을 순회하며 서브 트리의 크기를 찾는 함수가 요구된다.
코드는 다음과 같다.
struct centroid {
int N;
vi tree_size, vis, par;
vvi _edges, edges;
centroid(int N) : N(N), tree_size(N), vis(N), _edges(N), edges(N), par(N) {}
void add_edge(int u, int v) { _edges[u].pb(v); }
int get_size(int cur, int p) {
tree_size[cur] = 1;
for (int to: _edges[cur])if (to != p && !vis[to])tree_size[cur] += get_size(to, cur);
return tree_size[cur];
}
int get_centroid(int cur, int p, int cap) {
for (int to: _edges[cur]) if (to != p && !vis[to] && tree_size[to] * 2 > cap) return get_centroid(to, cur, cap);
return cur;
}
int build_tree(int cur, int p = -1) {
cur = get_centroid(cur, -1, get_size(cur, -1));
par[cur] = p, vis[cur] = 1;
for (int to: _edges[cur])if (!vis[to]) to = build_tree(to, cur), edges[cur].pb(to), edges[to].pb(cur);
return cur;
}
};
build_tree는 처음에 호출되는 분할 정복 함수이며, centroid를 반환한다.
get_centroid에서는 현재 서브 트리의 centroid를 찾으며 그것을 반환한다.
더 이상 방문할 노드가 없거나 모든 주변 노드들의 크기가 서브 트리의 크기의 2를 넘지 않으면 그냥 센트로이드라고 판단한다.
get_size 함수는 서브 트리의 크기를 계산한다.
모든 Centroid를 찾을 때까지 계속해서 호출되기 때문에 매번 tree_size를 $1$로 설정하면서 사용해야 한다.
연습 문제
Type 1: 트리를 분해해가는 테크닉을 이용한 분할 정복
어떤 Centroid $c$가 포함되는 모든 경로들을 검사한다.
이건 문제에 따라 $O(N)$이 될 수도, $O(N \log N)$이 될 수도 있다. 그만큼 전체 시간복잡도가 영향을 받는다.
이제 트리들을 $c$의 서브 트리들로 분해한다.
$c$가 포함되는 경로는 더 이상 안보게 되므로 더 작은 크기의 서브트리들에서 특정 경로에 대한 정답을 찾아갈 수 있다.
Centroid는 계속해서 트리를 최대한 효율적으로 검사할 수 있게 분해시키기 때문에 시간복잡도상으로 이득을 챙길 수 있다.
BOJ 5820 - 경주 이 문제를 보자.
트리에서 가중치의 합이 $K$인 경로 중 가장 짧은 것의 길이를 구하라는 문제이다.
정말 말도 안되는 쿼리지만, Centroid는 이를 가능케한다.
일단, 크기 $N$의 트리에서 어떤 정점 $c$(우리가 구한 Centroid가 될 것)를 거쳐가는 경로를 구하는 시간복잡도는 얼마일까?
놀랍게도 $O(N)$이다!
서브트리들을 순회하며 다른 서브트리들에서 $c$까지의 거리가 $K’$ 인 것 중 가장 최소 개수의 간선으로 갈 때 그 간선수를 저장해두면,
현재 서브트리를 순회하며 이전에 저장해둔 거리가 $K-K’$ 인 것의 값을 가지고 정답을 업데이트시켜줄 수 있기 때문이다.
현재 서브트리가 순회가 끝나면 현재 서브트리의 결과를 한번에 업데이트 해주면 된다.
그렇지 않으면 같은 서브트리에서 구간 가중치 합이 $K$가 되는 것까지 찾아져서 $c$를 거치는 경로가 아니기 때문이다.
대개 경로와 관련된건 두 가지 타입을 따로 계산해주는게 편할 수 있다.
- $c$가 경로의 시작과 끝에 포함되는 경우
- 그렇지 않은 경우
풀이 코드는 다음과 같다.
Type 2: Centroid Tree의 성질을 이용한 최적화
성질 2, 3을 상기해보자.
2- 센트로이드 트리에서 두 정점 $u, v$의 최소 공통 조상은 $\overline{uv}$ 경로를 분할한다.
사실 이건 센트로이드 트리가 만들어지는 과정을 생각해보면 직관적으로 그렇다고 알 수 있다.
3- 센트로이드 트리에서 어떤 정점 $u$에서 루트까지에 있는 정점들 $P_i$는 $u$에서 다른 정점으로의 경로와 관련된 쿼리에 사용될 수 있다.
2번 성질을 조금 응용해서 3번 성질이 도출된다.
다른 모든 정점과의 경로를 그 정점과의 센트로이드 트리의 $u-LCA-v$ 라고 생각했을때, 자신이 가질 수 있는 모든 $LCA$ 와의 어떠한 연산의 결과를 취해주는것 만으로 $u$ 에서 다른 모든 정점까지의 경로들에서 연산의 결과를 도출해낼 수 있다.

센트로이드 트리에서는 트리의 높이가 $O(\log N)$으로 제한되기 때문에 어떤 노드의 조상 노드는 최대 $O(\log N)$개 이다.
따라서 정점 $u$ 에서 다른 모든 정점과의 어떠한 연산값을 $O(\log N)$의 시간복잡도 덕을 보면서 취해줄 수 있다는 결론이 나온다.
BOJ 13514 - 트리와 쿼리 5
BOJ 13514 - 트리와 쿼리 5 이 문제는 성질 3을 이용하는 문제이다.
$1$번 쿼리는 $i$번 정점의 색을 반전시키는 쿼리이다.
센트로이드 트리에서 보자면 $i$번 정점과 다른 모든 정점들과의 경로는 $i$번 정점이 가지는 조상 노드들 중 하나를 무조건 거치기 때문에 센트로이드 트리에서 $O(\log N)$개의 조상 노드들의 값을 업데이트 시켜주는 것으로 충분하다.
$2$번 쿼리도 비슷하게 모든 조상 노드들에 대해 훑어주며 정답을 찾으면 된다.
이 문제에선 각 정점이 집합을 관리하고 각각 흰색 정점과의 거리들을 모두 저장하고 있으면, 쿼리 하나에 $O(\log ^2N)$이 걸려 문제를 충분히 해결할 수 있다.
BOJ 11933 - 공장들
이 문제도 성질 3을 이용하는 문제이다.
하지만 시간적으로 최적화가 조금 필요하다.
이 문제를 풀 때 내가 했던 실수는 센트로이드 트리에서의 부모와 자식의 거리차이를 기존 트리의 것을 그대로 사용해줬다는 것이다.
이 실수를 알아차리는데 너무 오래걸렸고 심지어 HLD 템플릿도 같은 정점에 쿼리가 들어가면 제대로 동작하지가 않아서 디버깅이 힘들었다.



Comments